Другой способ представления целых чисел — дополнительный код. Диапазон значений величин зависит от количества бит памяти, отведенных для их хранения. Например, величины типа Integer (все названия типов данных здесь и ниже представлены в том виде, в каком они приняты в языке программирования Turbo Pascal. В других языках такие типы данных тоже есть, но могут иметь другие названия) лежат в диапазоне от -32768 (-215) до 32767 (215 - 1) и для их хранения отводится 2 байта (16 бит); типа LongInt — в диапазоне от -231 до 231 - 1 и размещаются в 4 байтах (32 бита); типа Word — в диапазоне от 0 до 65535 (216 - 1) (используется 2 байта) и т.д.
Как видно из примеров, данные могут быть интерпретированы как числа со знаком, так и без знака. В случае представления величины со знаком самый левый (старший) разряд указывает на положительное число, если содержит нуль, и на отрицательное, если — единицу.
Вообще, разряды нумеруются справа налево, начиная с 0. Ниже показана нумерация бит в двухбайтовом машинном слове.
Дополнительный код положительного числа совпадает с его прямым кодом. Прямой код целого числа может быть получен следующим образом: число переводится в двоичную систему счисления, а затем его двоичную запись слева дополняют таким количеством незначащих нулей, сколько требует тип данных, к которому принадлежит число.
Например, если число 37(10) = 100101(2) объявлено величиной типа Integer (шестнадцатибитовое со знаком), то его прямым кодом будет 0000000000100101, а если величиной типа LongInt (тридцатидвухбитовое со знаком), то его прямой код будет 00000000000000000000000000100101. Для более компактной записи чаще используют шестнадцатеричное представление кода. Полученные коды можно переписать соответственно как 0025(16) и 00000025(16).
Дополнительный код целого отрицательного числа может быть получен по следующему алгоритму:
- записать прямой код модуля числа;
- инвертировать его (заменить единицы нулями, нули — единицами);
- прибавить к инверсному коду единицу.
Например, запишем дополнительный код числа -37, интерпретируя его как величину типа LongInt (тридцатидвухбитовое со знаком):
- прямой код числа 37 есть 00000000000000000000000000100101;
- инверсный код 11111111111111111111111111011010;
- дополнительный код 11111111111111111111111111011011 или FFFFFFDB(16).
При получении числа по его дополнительному коду прежде всего необходимо определить его знак. Если число окажется положительным, то просто перевести его код в десятичную систему счисления. В случае отрицательного числа необходимо выполнить следующий алгоритм:
- вычесть из кода числа 1;
- инвертировать код;
- перевести в десятичную систему счисления. Полученное число записать со знаком минус.
Примеры. Запишем числа, соответствующие дополнительным кодам:
- 0000000000010111. Поскольку в старшем разряде записан нуль, то результат будет положительным. Это код числа 23.
- 1111111111000000. Здесь записан код отрицательного числа. Исполняем алгоритм: 1) 1111111111000000(2) - 1(2) = 1111111110111111(2); 2) 0000000001000000; 3) 1000000(2) = 64(10).
Ответ: -64.
Вопрос 6 Системы счисления
Для удобства последующего преобразования дискретный сигнал подвергается кодированию (о кодировании см. в разделе Кодирование сигнала). Большинство кодов основано на системах счисления, причем использующих позиционный принцип образования числа, при котором значение каждой цифры зависит от ее положения в числе.
Примером позиционной формы записи чисел является та, которой мы пользуемся (так называемая арабская форма чисел). Так, в числах 123 и 321 значения цифры 3, например, определяются ее положением в числе: в первом случае она обозначает три единицы (т.е. просто три), а во втором – три сотни (т.е. триста).
Тогда полное число получается по формуле:
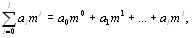
где l – количество разрядов числа, уменьшенное на 1,
i – порядок разряда,
m – основание системы счисления,
ai – множитель, принимающий любые целочисленные значения от 0 до m-1, и соответствующий цифре i-го порядка числа.
Например, для десятичного (m = 10) числа 345 его полное значение рассчитывается по формуле:
3*102 + 4*101 + 5*100 = 345.
Римские числа являются примером полупозиционной системы образования числа: так, в числах IX и XI знак I обозначает в обоих случаях единицу (признак непозиционной системы), но, будучи расположенным слева от знака X (обозначающего десять), вычитается из десяти, а при расположении справа – прибавляется к десяти. В первом случае полное значение числа равно 9, во втором – 11.
В современной информатике используются в основном три системы счисления (все – позиционные): двоичная, шестнадцатеричная и десятичная.
Двоичная система счисления используется для кодирования дискретного сигнала, потребителем которого является вычислительная техника. Такое положение дел сложилось исторически, поскольку двоичный сигнал проще представлять на аппаратном уровне. В этой системе счисления для представления числа применяются два знака – 0 и 1.
Шестнадцатеричная система счисления используется для кодирования дискретного сигнала, потребителем которого является хорошо подготовленный пользователь – специалист в области информатики. В такой форме представляется содержимое любого файла, затребованное через интегрированные оболочки операционной системы, например, средствами Norton Commander в случае MS DOS. Используемые знаки для представления числа – десятичные цифры от 0 до 9 и буквы латинского алфавита – A, B, C, D, E, F.
Десятичная система счисления используется для кодирования дискретного сигнала, потребителем которого является так называемый конечный пользователь – неспециалист в области информатики (очевидно, что и любой человек может выступать в роли такого потребителя). Используемые знаки для представления числа – цифры от 0 до 9.
Соответствие между первыми несколькими натуральными числами всех трех систем счисления представлено в таблице перевода:
| Десятичная система | Двоичная система | Шестнадцатеричная система |
| A | ||
| B | ||
| C | ||
| D | ||
| E | ||
| F | ||
Для различения систем счисления, в которых представлены числа, в обозначение двоичных и шестнадцатеричных чисел вводят дополнительные реквизиты:
· для двоичных чисел – нижний индекс справа от числа в виде цифры 2 или букв В либо b (binary – двоичный), либо знак B или b справа от числа. Например, 1010002 = 101000b = 101000B = 101000B = 101000b;
· для шестнадцатеричных чисел - нижний индекс справа от числа в виде числа 16 или букв H либо h (hexadecimal – шестнадцатеричный), либо знак H или h справа от числа. Например, 3AB16 = 3ABH = 3ABh = 3ABH = 3ABh.
Для перевода чисел из одной системы счисления в другую существуют определенные правила. Они различаются в зависимости от формата числа – целое или правильная дробь. Для вещественных чисел используется комбинация правил перевода для целого числа и правильной дроби.
Вопрос 7 В двоичной системе счисления арифметические операции выполняются по тем же правилам, что и в десятичной системе счисления, т.к. они обе являются позиционными (наряду с восьмеричной, шестнадцатеричной и др.).
Сложение
Сложение одноразрядных двоичных чисел выполняется по следующим правилам:
0 + 0 = 01 + 0 = 10 + 1 = 11 + 1 = 10В последнем случае, при сложении двух единиц, происходит переполнение младшего разряда, и единица переносится в старший разряд. Переполнение возникает в случае, если сумма равна основанию системы счисления (в данном случае это число 2) или больше его (для двоичной системы счисления это не актуально).
Сложим для примера два любых двоичных числа:
1101+ 101 ------ 10010Вычитание
Вычитание одноразрядных двоичных чисел выполняется по следующим правилам:
0 - 0 = 01 - 0 = 10 - 1 = (заем из старшего разряда) 11 - 1 = 0Пример:
1110- 101 ---- 1001Умножение
Умножение одноразрядных двоичных чисел выполняется по следующим правилам:
0 * 0 = 01 * 0 = 00 * 1 = 01 * 1 = 1Пример:
1110* 10------+ 0000 1110 ------ 11100Деление
Деление выполняется так же как в десятичной системе счисления:
1110 | 10 |----10 | 111---- 11 10---- 10 10---- 0Вопрос 8
Кодирование звука
На компьютере работать со звуковыми файлами начали в 90-х годах. В основе цифрового кодирования звука лежит – процесс преобразования колебаний воздуха в колебания электрического тока и последующая дискретизация аналогового электрического сигнала. Кодирование и воспроизведение звуковой информации осуществляется с помощью специальных программ (редактор звукозаписи).
Временная дискретизация – способ преобразования звука в цифровую форму путем разбивания звуковой волны на отдельные маленькие временные участки где амплитуды этих участков квантуются (им присваивается определенное значение).
Это производится с помощью аналого-цифрового преобразователя, размещенного на звуковой плате. Таким образом, непрерывная зависимость амплитуды сигнала от времени заменяется дискретной последовательностью уровней громкости. Современные 16-битные звуковые карты кодируют 65536 различных уровней громкости или 16-битную глубину звука (каждому значению амплитуды звук. сигнала присваивается 16-битный код)
Качество кодирование звука зависит от:
- глубины кодирования звука - количество уровней звука
- частоты дискретизации – количество изменений уровня сигнала в единиц






