Лекции Элементы аналитической геометрии
План лекций
Прямая на плоскости. Кривые II-го порядка: окружность, эллипс, гипербола, парабола, их канонические уравнения. Плоскость и прямая в пространстве. Основные задачи на прямую и плоскость в пространстве. Понятие об уравнении поверхности.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
- Метод координат: числовая прямая, координаты на прямой; прямоугольная (декартовая) система координат на плоскости; полярные координаты.
Рассмотрим какую-нибудь прямую. Выберем на ней направление (тогда она станет осью) и некоторую точку 0 (начало координат). Прямая с выбранным направлением и началом координат называется координатной прямой (при этом считаем, что единица масштаба выбрана).
Пусть М – произвольная точка на координатной прямой. Поставим в соответствии точке М вещественное число x, равное величине ОМ отрезка  : x=ОМ. Число x называется координатой точки М.
: x=ОМ. Число x называется координатой точки М.

Таким образом, каждой точке координатной прямой соответствует определенное вещественное число – ее координата. Справедливо и обратное утверждение: каждому вещественному числу x соответствует некоторая точка на координатной прямой, а именно такая точка М, координата которой равна x. Такое соответствие называется взаимно однозначным.
Итак, вещественные числа можно изображать точками координатной прямой, т.е. координатная прямая служит изображением множества всех вещественных чисел. Поэтому множество всех вещественных чисел называют числовой прямой, а любое число – точкой этой прямой. Около точки на числовой прямой часто указывают число – ее координату.
Две взаимно перпендикулярные оси Оx и Оy, имеющие общее начало О и одинаковую единицу масштаба, образуют прямоугольную (или декартовую) систему координат на плоскости.
Ось ОХ называется осью абсцисс, ось ОY – осью ординат. Точка О пересечения осей называется началом координат. Плоскость, в которой расположены оси ОХ и ОY , называется координатной плоскостью и обозначается Оxy.
Итак, прямоугольная система координат на плоскости устанавливает взаимно однозначное соответствие между множеством всех точек плоскости и множеством пар чисел, которое дает возможность при решении геометрических задач применить алгебраические методы. Оси координат разбивают плоскость на 4 части их называют четвертями, квадратными или координатными углами.
Полярная система координат состоит из некоторой точки О, называемой полюсом, и исходящего из нее луча ОЕ, называемого полярной осью. Кроме того, задается единица масштаба для измерения длин отрезков. Пусть задана полярная система координат и пусть М – произвольная точка плоскости. Обозначим через ρ – расстояние точки М от точки О, а через φ – угол, на который луч повернуть против часовой стрелки полярную ось для совмещения с лучом ОМ.

Полярными координатами точки М называют числа ρ и φ. Число Р считают первой координатой и называют полярным радиусом, число φ – второй координатой и называют полярным углом.
Точка М с полярными координатами ρ и φ обозначаются так: М(ρ;φ). Установим связь между полярными координатами точки и ее прямоугольными координатами. При этом будем предполагать, что начало прямоугольной системы координат находится в полюсе, а положительная полуось абсцисс совпадает с полярной осью.

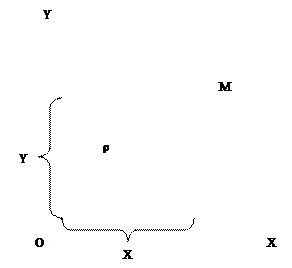

Пусть точка М имеет прямоугольные координаты X и Y и полярные координаты ρ и φ.
| |||
| |||
Эти формулы выражают прямоугольные координаты через полярные, а выражение полярных координат через прямоугольные следует из этих формул:
| |||
| |||
Формула  определяет два значения полярного угла, так как φ изменяется от 0 до 2π. Из этих двух значений угла φ выбирают то, при котором удовлетворяются равенства (1).
определяет два значения полярного угла, так как φ изменяется от 0 до 2π. Из этих двух значений угла φ выбирают то, при котором удовлетворяются равенства (1).
- Расстояние между двумя точками.
Теорема. Для любых двух точек М1 (x1 ;y1) и М2 (x2; y2) плоскости расстояние α между ними выражается формулой:
| |||
| |||
Доказательство.
Опусти из точек М1 и М2 перпендикуляры М1В и М1А,. так как (x2; y2). По теореме, если М1 (х1) и М2 (х2) – любые две точки и α– расстояние между ними, то α =|x2 - x1|:
|М1 К|=|x2 - x1|; |М2 К|=|y2 - y1|.




- Площадь треугольника.
|
|
Доказательство.
 |

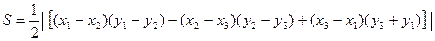 ,
,
из которой после несложных преобразований следует формула (3).
- Деление отрезка в данном отношении.
|
Число λ, определяемое равенством, называется отношением,
в котором, точка М делит отрезок М1М2 .
Задача о делении отрезка в данном отношении состоит в том, чтобы по данному отношению λ и данным координатам точек М1 и М2 найти координаты точки М.
|
|
,
где (x1;y1) – координаты точки М1, (x2;y2) – координаты точки М2.
Доказательство.

Пусть М1М2 не перпендикулярны оси OX. Опустим М1P ^ OX, MP ^ OX, М2Р2 ^ ОХ.
На основании теоремы элементарной геометрии о пропорциональности отрезков прямых, законченных между параллельными прямыми, имеем  . Но по теореме (если М1 (x1) и M2(x2) – любые две точи и α – расстояние между ними, то
. Но по теореме (если М1 (x1) и M2(x2) – любые две точи и α – расстояние между ними, то  )
)
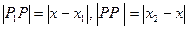 . Так как числа (x - x1) и (х2 - х) имеют один и тот же знак (при х1<x2 они положительны, а при х1>x2 отрицательны), то
. Так как числа (x - x1) и (х2 - х) имеют один и тот же знак (при х1<x2 они положительны, а при х1>x2 отрицательны), то  . Поэтому
. Поэтому  , откуда
, откуда  . Если М1М2 ^ OX, то x1 = x2= x и эта формула очевидно, верна. Вторая формула находится аналогично.
. Если М1М2 ^ OX, то x1 = x2= x и эта формула очевидно, верна. Вторая формула находится аналогично.
|
 , то λ=1 и по формулам (5) получаем:
, то λ=1 и по формулам (5) получаем:
.
Таким образом, каждая координата середины отрезка равна полусумме соответствующих координат.
- Прямая линия на плоскости
- уравнение прямой с угловым коэффициентом;
Пусть дана некоторая прямая, не перпендикулярная, оси ОХ. Назовем углом наклона данной прямой к оси ОХ угол α, на который нужно повернуть ось ОХ, чтобы положительное направление совпало с одним из направлений прямой. Тангенс угла наклона прямой к оси ОХ называют угловым коэффициентом этой прямой и обозначают буквой k.
| |||
| |||
Выведем уравнение данной прямой, если известны ее k и величина b отрезок ОВ, которой она отсекает на оси ОУ.

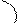






|
|
 . Но NM=CM-CN=CM-OB=y-b, BN=x => учитывая (1), получаем, что точка М (х; у) С на данной прямой <=>, когда ее координаты удовлетворяют уравнению:
. Но NM=CM-CN=CM-OB=y-b, BN=x => учитывая (1), получаем, что точка М (х; у) С на данной прямой <=>, когда ее координаты удовлетворяют уравнению: 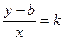 =>
=>
Уравнение (2) называют уравнением прямой с угловым коэффициентом. Если K=0, то прямая параллельна оси ОХ и ее уравнение имеет вид y = b.
- уравнение прямой, проходящей через две точки;
| |||
| |||
Пусть даны две точки М1 (х1; у1) и М2 (х2; у2). Приняв в (3) точку М (х; у) за М2 (х2; у2), получим у2-у1=k(х2 - х1). Определяя k из последнего равенства и подставляя его в уравнение (3), получаем искомое уравнение прямой:  . Это уравнение, если у1≠ у2, можно записать в виде:
. Это уравнение, если у1≠ у2, можно записать в виде:
Если у1 = у2 , то уравнение искомой прямой имеет вид у = у1. В этом случае прямая параллельна оси ОХ. Если х1 = х2, то прямая, проходящая через точки М1 и М2, параллельна оси ОУ, ее уравнение имеет вид х = х1.
- уравнение прямой, проходящей через заданную точку с данным угловым коэффициентом;
|
|
Замечание. Если прямая проходит через точку М1 (х1;у1) перпендикулярна оси ОХ, т.е. ее угловой коэффициент обращается в бесконечность, то уравнение прямой имеет вид
х – х1 = 0. Формально это уравнение можно получит из уравнения (3), если разделить (3) на k и затем устремить k к ∞.
- общее уравнение прямой, частные случаи;
|
|
и, обратно, уравнение (5) при произвольных коэффициентах А, В, С (А и В ≠ 0 одновременно) определяет некоторую прямую в прямоугольной системе координат Оху.
Уравнение этой прямой имеет вид х = α, т.е. также является уравнение первой степени вида (5), где А = 1, В = 0, С = - α. Тем самым доказано первое утверждение.
Докажем обратное утверждение. Пусть дано уравнение (5), причем хотя бы один из коэффициентов А и В ≠ 0.
Если В ≠ 0, то (5) можно записать в виде  . Пологая
. Пологая  , получаем уравнение у = kx + b, т.е. уравнение вида (2) которое определяет прямую.
, получаем уравнение у = kx + b, т.е. уравнение вида (2) которое определяет прямую.
Если В = 0, то А ≠ 0 и (5) принимает вид 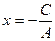 . Обозначая
. Обозначая 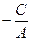 через α, получаем
через α, получаем
х = α, т.е. уравнение прямой перпендикулярное Ох.
Линии, определяемые в прямоугольной системе координат уравнением первой степени, называются линиями первого порядка.
Уравнение вида Ах + Ву + С = 0 является неполным, т.е. какой – то из коэффициентов равен нулю.
1) С = 0; Ах + Ву = 0 и определяет прямую, проходящую через начало координат.
2) В = 0 (А ≠ 0); уравнение Ах + С = 0 и определяет прямую параллельную Оу.
3) А = 0 (В ≠ 0); Ву + С = 0 и определяет прямую параллельную Ох.
|
|
Уравнение (6) называется уравнением прямой «в отрезках». Числа а и b являются величинами отрезков, которые прямая отсекает на осях координат. Эта форма уравнения удобна для геометрического построения прямой.
- Угол между двумя прямыми.



Рассмотрим две прямые L 1 и L2. Пусть уравнение L1 имеет вид y = k1x + b1, где
|
, или
|
(1)
Формула (1) определяет один из углов между прямыми. Второй угол равен π – φ.
- Условия параллельности и перпендикулярности двух прямых.
|
Таким образом, условием параллельности двух прямых является равенство их угловых коэффициентов.
|
 , то из (1) находим ctg φ2
, то из (1) находим ctg φ2  . В этом случае
. В этом случае  и 1 + k2k1 = 0 =>.
и 1 + k2k1 = 0 =>.
Таким образом, условия перпендикулярности двух прямых состоит в том, что их k обратны по величине и противоположны по знаку.
- Взаимное расположение двух прямых на плоскости.
Пусть прямые L 1 и L2 заданы уравнениями:  (10)
(10)
Решая эту систему, найдем:  .
.
Пусть A1B2 – A2B1 ≠ 0, тогда найденные формулы дают решение системы (10). Это значит, что L 1 не параллельна L2, L1 ∩ L2 = точке (x; y). Пусть теперь A1B2 – A2B1 ≠ 0. Возможны два случая:
1) A2C1 – A1C2 = 0 и B1C2 – B2C1 = 0;
2) A2C1 – A1C2 ≠ 0 (B1C2 – B2C1 ≠ 0).
В первом случае имеем А2 = МА1, В2 = МВ1, С2 = МС1 или  , где М≠ 0 - некоторое число. Это означает,что коэффициенты уравнений пропорциональны следовательно второе уравнение получается из первого умножением на число М. В этом случае L 1 и L2 совпадают, т.е. уравнения определяют одну и ту же прямую.
, где М≠ 0 - некоторое число. Это означает,что коэффициенты уравнений пропорциональны следовательно второе уравнение получается из первого умножением на число М. В этом случае L 1 и L2 совпадают, т.е. уравнения определяют одну и ту же прямую.
Во втором случае, если, например, A2C1 – A1C2 ≠ 0, то допустив, что система имеет решение (х0; у0), получим противоречие A2C1 – A1C2 = 0, что противоречит предположению. Таким образом, система (10) решения не имеет. В этом случае прямые L 1 и L2 не имеют точек пересечения, т.е. они параллельны.
Итак, две прямые на плоскости либо пересекаются в одной точке, либо совпадают, либо параллельны.
- Расстояние от точки до прямой.
Теорема. Расстояние α от данной точки М (х0; у0) до прямой L, заданной уравнением Ах + Ву + С = 0 на плоскости, определяется формулой:
|
(11)
Рассмотрим на прямой L две " точки E и F c координатами (х1; у1) и (х2; у2).

- Линии второго порядка:
- общее уравнение линий второго порядка;
|
(1)
А, В, С одновременно не равны нулю.
- эллипс, определение и вывод канонического уравнения;
Определение. Эллипсом называется множество всех точек плоскости, для которых сумма расстояний от двух данных точек, называемых фокусами, есть величина постоянная, большая расстояния между фокусами.
Для вывода уравнения эллипса введем на плоскости прямоугольную систему координат так, чтобы фокусы эллипса лежали на оси Ох, а начало координат делило бы расстояние между фокусами пополам. Выведем уравнение эллипса в выбранной системе координат.
Обозначим фокусы эллипса через F1 и F2. Пусть М – произвольная точка эллипса.  обозначим через 2с, сумма расстояний от точки М до фокусов – через 2а.
обозначим через 2с, сумма расстояний от точки М до фокусов – через 2а.

Так как по определению  , то 2а > 2с или а > c. Обозначим через r1 и r2 расстояние от точки М до F1 и F2. Числа r1 и r2 называются фокальными радиусами точки М. Из определения следует, что точка М (х; у) С на данном эллипсе в том и только в том случае, когда
, то 2а > 2с или а > c. Обозначим через r1 и r2 расстояние от точки М до F1 и F2. Числа r1 и r2 называются фокальными радиусами точки М. Из определения следует, что точка М (х; у) С на данном эллипсе в том и только в том случае, когда
r1 + r2 = 2 a (6).
Чтобы получить искомое уравнение эллипса, нужно в равенстве (6) заменить переменные r1 и r2 их выражениями через координаты х и у.
Так как F1 и F2 расположены на оси Ох симметрично относительно (0; 0), то F1(-C;0), F2(C; 0). Применяя формулу (1) Bυ2, находим 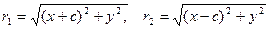 (7)
(7)
Подставим (7) в (6):
|
(8) –
искомое уравнение эллипса. Это уравнение обычно приводят к более простому виду. Для этого перенесем второй корень (3) в правую часть уравнения, а затем возведем обе части равенства в квадрат:  .
.
 (9)
(9)
Снова возведем обе части равенства в квадрат:  (10)
(10)
Введем новую величину:  (11)
(11)
Так как по условию a > c, то 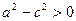 и, следовательно, b > 0. Из равенства (11) имеем
и, следовательно, b > 0. Из равенства (11) имеем  , поэтому уравнение (10) можно записать в идее:
, поэтому уравнение (10) можно записать в идее:

|
(12) – коническое (простейшее) уравнение эллипса.
Убедимся в том, что уравнение (8) и (12) равносильны. Для этого достаточно показать, что величины r1 и r2 для " точки, координаты которой удовлетворяют (12), удовлетворяют (6). Пусть координаты " точки удовлетворяют уравнению (12) (х; у). Тогда, подставляя в выражение (7) для r1 значение  (из (12)),
(из (12)),  . Так как
. Так как  (из (12)) и
(из (12)) и  , то
, то  и поэтому
и поэтому  . Аналогично,
. Аналогично,  . Складывая почленно эти равенства, получаем соотношение (6). Т.о. (12) – уравнение эллипса.
. Складывая почленно эти равенства, получаем соотношение (6). Т.о. (12) – уравнение эллипса.
- гипербола, определение и вывод канонического уравнения;
Определение. Гиперболой называется множество всех точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами, есть величина постоянная, меньшая расстоянию между фокусами. Для вывода уравнения гиперболы введем на плоскости прямоугольную систему координат ток чтобы F1C Ox и F2 C Ox и OF1 = OF2.
|

 (13)
(13)
Чтобы получить искомое уравнение гиперболы, нужно в (13) заменить r1 и r2 их выражениями через координаты x и у. F1 (-C; 0), F2 (C; 0).
По формуле (1) Bυ2 находим:
 (14)
(14)
Подставляя эти выражения в равенство (9), получаем:
 (15) –
(15) –
искомое уравнение гиперболы. Перенесем второй корень в правую часть уравнения, а затем возведем обе части в квадрат: 
 (16)
(16)
Снова возведем обе части уравнения в квадрат:  (17)
(17)
Введем новую величину  (18).
(18).
Так как с > a, то  и b > 0. Из (18) имеем
и b > 0. Из (18) имеем  . Уравнение (17) примет вид
. Уравнение (17) примет вид  или
или
|
(19) - коническое уравнение гиперболы.

- парабола, определение и вывод канонического вида;
Определение. Параболой называется множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.

Для вывода уравнения параболы введем на плоскости прямоугольную систему координат так, чтобы Ох проходила через F перпендикулярно директрисе, и будем считать положительным направлением направление от директрисы к фокусу; начало координат расположим посередине между F и директрисой.
Пусть М (х; у) – произвольная точка параболы. Обозначим  , через d - расстояние от М до директрисы, а через p – расстояние от F до директрисы. Величину p называют параметром параболы. Т. М будет С на данной параболе в том случае когда
, через d - расстояние от М до директрисы, а через p – расстояние от F до директрисы. Величину p называют параметром параболы. Т. М будет С на данной параболе в том случае когда
r = d (20)
Чтобы получить искомое уравнение, нужно в (20) заменить переменные r и d их выражениями через координаты х и у.  ; поэтому по формуле (1) находим:
; поэтому по формуле (1) находим:
 (21).
(21).
Обозначим через Q основание перпендикуляра, опущенного из M на директрису  следовательно и из (1) получаем:
следовательно и из (1) получаем:
 (22).
(22).
|
- искомое уравнение параболы (23).
|
 или каноническое уравнение параболы (24).
или каноническое уравнение параболы (24).
Проверим, что (24) после возведения в квадрат обеих частей равенства (23) не приобрело «лишних» корней. Для этого достаточно показать, что для любой точки, координаты х и у которой удовлетворяют уравнению (24), выполнено соотношение (20). Действительно, из уравнения (24) следует, что  , поэтому для точек с неотрицательными абсциссами
, поэтому для точек с неотрицательными абсциссами  . Подставляя значение у2 из (24) в (21) для r и учитывая, что
. Подставляя значение у2 из (24) в (21) для r и учитывая, что  , получаем, что
, получаем, что  , т.е. r = d, что и требовалось доказать.
, т.е. r = d, что и требовалось доказать.










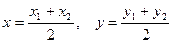










 . Так как, по определению,
. Так как, по определению,
 , то 2а < 2с или а < c. Числа
, то 2а < 2с или а < c. Числа
 и
и  называются фокальными радиусами т. М и обозначаются через r1 и r2. Из определения следует, что т. М(х; у) С на данной гиперболе в том и только в том случае, когда
называются фокальными радиусами т. М и обозначаются через r1 и r2. Из определения следует, что т. М(х; у) С на данной гиперболе в том и только в том случае, когда  следовательно
следовательно




