Размеры колес, а также всего зацепления, зависит от числа зубьев колёс z1=13, z2=45, от модуля зацепления m=4, общего для обоих колёс, а также от метода их обработки.
Произведём расчёт основных геометрических размеров зубчатых колёс.
Таблица 2.1
| Наименование | Обозначение | Формула |
| Шаг зацепления по делительной окружности | Р | P=π*m=3.14*4=12,56 |
| Радиус делительной окружности | r1,2,мм | 
|
| Радиусы основных окружностей | rb1,2,мм | 
|
| Коэффициент суммы смещений | X∑ | X∑=x1+x2 X∑=0,235+0=0,235 |
| Толщина зуба по делительной окружности | s1,2,мм | 
|
| Угол зацепления | αw | 21˚ |
| Межосевое расстояние | аw мм | 
|
| Коэффициент воспринимаемого смещения | у | 
|
| Коэффициент уравнительного смещения | ∆у | ∆у=Х∑-у ∆у=0,235-0,19=0,045 |
 |
 Радиусы окружностей впадин
| rf1,2, мм | 
|
| Радиусы окружностей вершин | ra1,2, мм | 
|
| Радиусы начальных окружностей | rw1,2, мм | 
|
| Глубина захода зубьев | hd, мм | hd=(2*ha*-∆y)*m hd=(2*1-0,19)*4=7,24 |
| Высота ножки зуба | hf, мм | hf=h+(1+c)=1.25*m hf=1+0.25*4=8 |
Постоянные
  
cosα=0.9397,
tgα=0.36397,
π=3.14
|
Подсчитав все размеры элементов зацепления по формулам, приведённым выше, приступаем к вычерчиванию зубчатого зацепления. Определяем активную часть линии зацепления, затем строим рабочие участки профилей зубьев. Те участки профилей зубьев, которые участвуют в зацеплении, называют рабочими.
2.1 Расчёт планетарной передачи
Принимаю рекомендуемое передаточное отношение
Для подбора чисел зубьев колёс 1,2,3 пользуюсь условием «3С»-сборки, соседства, соостности.
1Условие соостности:
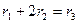
Принимаю:
Тогда:
Условие выполнено
2Условие соседства
,где
количество сотелитов (от 1 до 7)
принимаю 
3Условие сборки
, где
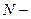любое натуральное число
С другой стороны передаточное отношение от колеса 1 к водиле Н при неподвижном колесе 3 определится по формуле:
Определяю размеры зубчатых колёс:
Согласно полученным значениям вычерчиваю схему в масштабе
Построим треугольник распределения скоростей для каждого из колес редуктора.
Отложим скорость точки А вправо. Скорость центра колес 1 и 3 равна нулю. Скорость точки В тоже равна нулю. Соединим точку А’ с О1 и получим треугольник скоростей для колеса 1. Соединим точку А’ c В и получим треугольник скоростей для колеса 2.
Теперь определим скорость водила. Проведем горизонталь из точки О2 до прямой 2. Получим скорость центра второго колеса. Соединим точку О2’ с О1 и получаем треугольник скоростей для водила.
Так как колесо А жестко связано с водилом, то треугольник скоростей для водила будет являться треугольником скоростей для колеса А.
Проведем горизонталь из точки С до прямой А. Получим скорость точки С. Скорость центра колеса В равна нулю. Соединим точки С’ и Ов и получим треугольник скоростей для колеса В.
По построенным треугольникам скоростей можно определить передаточное отношение редуктора.
Все описанные построения приведены в приложении
 |
