Владимирова Л.В.
Многокритериальная оптимизация в прикладных задачах
I. Моделирование случайных величин
- Теорема о моделирование непрерывной случайной величины. Формула моделирования по заданной плотности. Пример.
- Моделирование равномерно распределённой случайной величины в заданном промежутке. Моделирование случайного равномерно распределённого вектора в заданном параллелепипеде. Алгоритм моделирования случайного равномерно распределённого вектора в заданной области.
3. Теорема о связи плотностей в различных системах координат. Переход из декартовой в полярную систему координат и соответствующее преобразование плотности. Формулы моделирования равномерно распределённой случайной точки в круге.
- Приближённое моделирование случайной нормально распределённой величины (
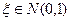). Основание для получения такой формулы. Понятие центрированной и нормированной случайных величин. Формула моделирования для 
. - Моделирование случайного двумерного нормально распределённого вектора
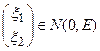. - Моделирование случайного
-мерного нормально распределённого вектора 
и алгоритм получения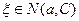 
. - Метод Неймана для моделирования случайных величин с заданной плотностью. Соответствующая теорема и алгоритм моделирования.
II. Метод Монте-Карло для вычисления интегралов
8. Метод Монте-Карло для приближенного вычисления интеграла с использованием реализаций случайного равномерно распределенного вектора в области интегрирования.
9. Метод Монте-Карло для приближенного вычисления интеграла для случая, когда подынтегральная функция является произведением двух функций, одна из которых используется в качестве плотности распределения узлов в области интегрирования.
III. Оптимизация одномерной и многомерной функций
10. Общая постановка задачи поиска минимума одномерной функции. Унимодальная функция. Удачная тройка чисел. Алгоритм поиска трёх удачных точек.
11. Метод парабол. Нахождение минимума параболы проходящей через три удачные точки. Теорема о положении минимума параболы между двумя крайними точками из трех удачных точек.
12. Направленный метод поиска минимума многомерной функции. Общая схема методов спуска. Градиентный метод. Метод наискорейшего спуска. Применения методов одномерной минимизации для нахождения шага по градиентному спуску.
IV. Случайный поиск экстремума функции
- Простейший случайный поиск. Алгоритм и теорема о сходимости метода.
- Случайный поиск с использованием нормального распределения. Идея метода. Алгоритм метода. Плотность распределения случайных точек на нулевой итерации и на других итерациях. Формулы для получения элементов матрицы ковариаций (точная и приближённая). Теорема о сходимости метода.
