Оценочные средства для текущего контроля успеваемости, промежуточной аттестации по итогам освоения дисциплины и учебно-методическое обеспечение самостоятельной работы студентов

Каждый модуль курса завершается письменным промежуточным тестированием, который проводится в течение 1 академического часа. Варианты тестов составляются из контрольных вопросов к отдельным модулям. Каждый вариант состоит не менее чем из 3-5 вопросов (в зависимости от сложности последних), на которые студент должен дать краткий обоснованный ответ. Список возможных вопросов приведен для каждого модуля ниже.

На практических занятиях студенты решают задачи по курсу совместно с преподавателем. Другая часть задач предлагается студентам для самостоятельного решения.

Контрольные работы №1, №2 проводятся по домашним задачам, которые решаются студентами самостоятельно.

Примеры задач

№1

Область занята плазмой с диэлектрической проницаемостью , при – вакуум. Показать, что вдоль границы плазма-вакуум может распространяться поверхностная волна, напряженность поля в которой затухает экспоненциально при удалении от границы. Найти область частот существования этой волны. При каких частотах она является медленной (). Какова при этом ее скорость?

№2

Найти тензор комплексной диэлектрической проницаемости плазмы, находящейся в постоянном магнитном поле . Плазму рассматривать в линейном приближении как электронный газ, частицы которого за счет соударений движутся с коэффициентом трения , где – эффективная частота столкновений.

№3

Используя выражение для диэлектрической проницаемости холодной плазмы , где - квадрат частоты плазменных колебаний, исследовать дисперсию распространяющейся в такой однородной плазме волны с электрическим полем . Рассмотреть случаи, когда волна является продольной (вектор параллелен и ) и когда волна является поперечной (). Найти магнитное поле этих волн.

№4

Исходя из уравнения непрерывности, которое для потенциала скоростей сводится к уравнению Лапласа , исследовать траекторию движения частицы при распространении монохроматической плоской волны малой амплитуды в бесстолкновительной плазме.

№5

Получить выражение для частоты ленгмюровских (плазменных) электронных колебаний в однородной по плотности неограниченной плазме. Для этого рассмотреть случайное одномерное смещение на малое расстояние ее электронной компоненты в области протяженностью относительно неподвижной ионной компоненты. Тепловым движением и столкновениями пренебречь.

№6

Если пренебречь тепловым движением и столкновениями частиц плазмы, при распространении монохроматической плоской электромагнитной волны параметрами плазмы можно считать и , где - квадрат частоты плазменных колебаний электронов. Рассмотреть поле монохроматической поперечной волны и исследовать поведение средней плотности потока энергии при и при .

№7

Формулы для скоростей волн: продольной и поперечной 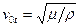, где - плотность упругого твердого тела, преобразовать так, чтобы вместо коэффициентов Ламе и в них вошли модуль Юнга и коэффициент Пуассона . Установить интервал изменения отношения , учитывая, что .

№8

Скорость звука в воздухе с плотностью можно принять равной . Звук, вызывающий болевое ощущение, имеет интенсивность (плотность потока энергии) . Какую долю атмосферного давления составляет в этом случае акустическое давление ?

№9

Едва слышимый звук в воздухе имеет интенсивность, которая составляет от стандартной . Рассчитайте амплитуду смещения частиц и амплитуду их скорости для частоты 500 Гц. Сравните амплитуду смещения с длиной свободного пробега молекулы и диаметром молекулы , а амплитуду скорости – со средней тепловой скоростью (~ скорость звука). Почему мы не слышим шума хаотического движения молекул воздуха?

№10

Проверить, что волны

1. плоская и

2. сферическая при

удовлетворяют волновому уравнению , а

3. волна цилиндрическая удовлетворяет этому уравнению при больших .

№11

Периодическая функция может быть представлена в виде ряда Фурье, допускающего следующие формы записи

.

Выразить амплитуды гармоник и начальные фазы гармоник через амплитудные коэффициенты других форм разложения. Принять во внимание, что для вещественной функции величины - комплексные.

№12

Волновой пакет состоит из двух компонент с длинами волн и , причем . Покажите, что число длин волн, умещающихся между двумя соседними нулями огибающей, приблизительно равно .

№13

Относительная диэлектрическая проницаемость газа на длине волны описывается выражением , где A, B, D – постоянные, c – скорость света в свободном пространстве (вакууме), а - его фазовая скорость в газе. Покажите, что групповая скорость удовлетворяет соотношению .

№14

В гармонически меняющимся с частотой поле относительная диэлектрическая проницаемость плазмы в пренебрежении столкновениями определяется соотношением , где - квадрат частоты плазменных колебаний электронов. Фазовая скорость поперечной электромагнитной волны связана со скоростью света в пустоте соотношением . Получите дисперсионную зависимость и изобразите дисперсионную характеристику. Как ведут себя фазовая и групповая скорости при ? Как меняется зависимость поля волны ~ при ?

№15

Сохранив в разложении дисперсионной зависимости три члена разложения в ряд по приращению волнового вектора , показать, что понятие о волновом пакете сохраняет смысл только на не слишком больших расстояниях , удовлетворяющих условию . Для простоты рассмотреть случай, когда пакет состоит из двух гармонических составляющих одинаковой амплитуды с волновыми числами .

№16

Показать, что в анизотропной среде с и тензором диэлектрической проницаемости дисперсионное уравнение для волны вида 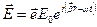( - единичный вектор) имеет вид . Найти вектор групповой скорости. Указание: Предварительно умножить скалярно дисперсионное уравнение на единичный вектор .

№17

Рассмотреть спектр импульса показать, что область частот , дающая существенный вклад в энергию импульса, удовлетворяет условию (теорема о ширине частотной полосы). Покажите, что в среде без дисперсии при распространении волнового пакета, соответствующему такому импульсу, между протяженностью волнового пакета и интервалом волновых чисел , дающих существенный вклад в волновой пакет, имеется связь .

№18

Покажите, что фазомодулированный сигнал при может быть приближенно представлен в виде . Сигнал передается по линии с дисперсией так, что на некотором расстоянии от источника к фазовым углам и добавляется фазовый сдвиг (запаздывание) на . Каким станет сигнал в этом месте?

№19

Вдоль струны с линейной плотностью и натяжением в положительном направлении оси Х, с которой струна совпадает в состоянии покоя, распространяется волна плоского профиля. Ограничиваясь малыми углами наклона профиля волны, вычислить поперечный импеданс струны, определяемый как отношение поперечной составляющей силы к поперечной скорости. Указание: Учитывая, что волна в струне является стационарной, использовать известную для такой волны связь между производными смещения по координате и времени.

№20

В трубе длиной L образовались стоячие акустические волны. Записать выражение для зависимости смещения частиц от координаты X и времени t и найти спектр собственных частот для двух случаев

1. оба конца трубы открыты;

2. один конец открыт, а другой – закрыт.

Акустическое давление на открытом конце принять равным нулю.

№21

При закручивании стержня с закрепленным концом моментом сил K, приложенным к другому концу, в приближении закона Гука имеется линейная связь между этим моментом и углом закручивания единицы длины стержня: , где С – крутильная жесткость стержня. Считая известным геометрический момент инерции I поперечного сечения стержня относительно центра инерции, получить уравнение для волн кручения, рассматривая угловое смещение сечения относительно его положения равновесия. Для круглого стержня радиуса R найти крутильную жесткость и вычислить скорость крутильных волн. Плотность материала стержня равна , модуль сдвига - .

№22

Вывести уравнение, описывающее волны в мембране – пленке, не оказывающей сопротивления сдвигу и изгибу. Поверхностная плотность мембраны - . Принимая отклонения от направления Z мембраны от положения равновесия (плоскость OXY) малыми, принять натяжение T (сила, отнесенная к единице длины контура на мембране) постоянным. Указания: воспользоваться теоремой Грина , применив ее к малой площадке на мембране .

№23

Отрезок струны L с линейной плотностью и натяжением T закреплен на концах. Найти частоты его собственных колебаний.

№24

Получить уравнения для частот собственных изгибательных колебаний стержня длины L для случаев:

1. оба конца свободны (низкочастотный кварцевый резонатор);

2. один конец заделан, другой – свободен (камертон).

Масса единицы длины стержня - , изгибательная жесткость (коэффициент пропорциональности между изгибающим упругим моментом и кривизной оси стержня) – С. Общее решение для монохроматической стоячей волны (опуская ) искать в виде .

№27

Вывести дисперсионное уравнение продольных плазменных волн, учитывая тепловое движение электронной компоненты, создающей давление , где и соответственно концентрация, и температура электронов. Движением ионов и столкновениями пренебречь. Для описания движения электронной компоненты использовать линеаризованные уравнения гидродинамики. Сжатие электронной компоненты считать адиабатическим и учитывать только одну (продольную) степень свободы электрона (частота волны велика по сравнению с частотой столкновений и за период волны энергия не успевает равномерно распределиться между степенями свободы).

№28

Получить дисперсионное уравнение, волновое сопротивление, построить дисперсионную характеристику зависимости от частоты волнового сопротивления для следующей длинной линии. (На схеме приведены их погонные параметры)

№29

Получить дисперсионное уравнение, волновое сопротивление, построить дисперсионную характеристику зависимости от частоты волнового сопротивления для следующей длинной линии. (На схеме приведены их погонные параметры)

№30

Получить дисперсионное уравнение, волновое сопротивление, построить дисперсионную характеристику зависимости от частоты волнового сопротивления для следующей длинной линии. (На схеме приведены их погонные параметры)

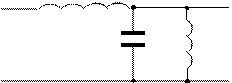№31

Получить дисперсионное уравнение, волновое сопротивление, построить дисперсионную характеристику зависимости от частоты волнового сопротивления для следующей длинной линии. (На схеме приведены их погонные параметры)

№32

Получить дисперсионное уравнение, волновое сопротивление, построить дисперсионную характеристику и зависимости от частоты волнового сопротивления для следующей длинной линии. (На схеме приведены их погонные параметры)

№33

Дисперсионное уравнение магнитогидродинамических (альвеновских) волн, распространяющихся в бесстолкновительной плазме с плотностью , помещенной в постоянное магнитное поле имеет вид:

.

Вычислить вектор групповой скорости этих волн. Совпадает ли он с направлением волнового вектора?

№34

Для длинной линии с погонными продольным сопротивлением и проводимостью найти дисперсионное уравнение и волновое сопротивление. Когда в линии без потерь существуют распространяющиеся волны (условие пропускания)? Каким является волновое сопротивление в области пропускания и в области непропускания?

2.5. Материально-техническое обеспечение дисциплины "Физика волновых процессов".

 

Требования к аудиториям (помещениям, местам) для проведения занятий.

Стандартно оборудованные лекционные аудитории. Для проведения отдельных занятий (по заявке) – выделение компьютерного класса, а также аудитории для проведения интерактивных лекций: видеопроектор, экран настенный, др. оборудование.

 

Требования к специальному программному обеспечению.

При использовании электронных учебных пособий каждый обучающийся во время занятий и самостоятельной подготовки должен быть обеспечен рабочим местом в компьютерном классе с выходом в Интернет и корпоративную сеть факультета.

 

Требования к перечню и объему расходных материалов.

Фломастеры цветные, губки, бумага формата А4, канцелярские товары, картриджи принтеров, диски, флеш-накопители и др. в объеме, необходимом для организации и проведения занятий, по заявкам преподавателей, подаваемым в установленные сроки.

Учебно методический комплекс составлен в соответствии с требованиями ФГОС ВПО с учетом рекомендаций и ПрООП ВПО по направлению подготовки 011800 – Радиофизика и профилю подготовки – физика радиоволн

 

Учебные модули.

Содержание модуля 1.

Материал модуля 1 включает в себя введение в дисциплину, изложение основных понятий и методов, которые используются при описании распространения волн различной физической природы в средах с различными свойствами, иллюстрацию на простейших одномерных и многомерных примерах предложенных общих подходов к изучению волновых полей. Основное внимание уделяется одномерным линейным свободно распространяющимся волнам в различных средах. Модуль 1 является базовым для всех остальных модулей, так как в нем излагаются основные понятия, явления, подходы к описанию волновых процессов, которые необходимы для понимания сложных явлений, сопровождающих распространение волн в линейных и нелинейных средах.

Комплексная цель модуля 1 – сформулировать основные цели и задачи курса; познакомить с физическими понятиями и подходами, которые используются при описании волн вне зависимости от их природы и среды, в которой развивается волновой процесс.