Теорема Безу
…
Теорема обобщенной ассоциативности - Пусть 
- векторы из V, тогда для любого 
Теорема обобщенной коммутативности – Пусть 
перестановка чисел 1,2,…,n, и пусть 
- векторы из V, тогда
Теорема обобщенной дистрибутивности – Пусть 
числа из F и пусть 
векторы из V. Тогда
1) 
2) 
Линейное пространство – множество V над полем F будем называть линейным пространством если:
a+(b+c) = (a+b) + c
1 
( 
Подпространство – Пусть V – линейное пространство над полем F и пусть W 
V, тогда W – подпространство V, если оно само является линейным пространством над полем F. W≠Ø. Т. W подпространство V тогда и только тогда, когда если a 
W и b W, то a+b W, и если α F, a W αa W.
Система векторов – произвольная конечная последовательность векторов из пространства V.
Линейная комбинация – Вектор b называется линейной комбинацией векторов 
, если существуют такие числа 
, что b=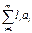 
Линейная оболочка векторов системы – множество всех линейных комбинаций векторов системы.
Линейная выразимость – говорят, что первая система линейно выражается через вторую систему, если каждый вектор второй системы выражается через вектора первой системы. 
ó 
Эквивалентные системы векторов – Две системы эквивалентны, если каждая из них линейно выражается через другую. Критерий эквивалентности. Две системы эквивалентны ó 
=
Свойства эквивалентности: 1. Рефлексивность. { 
}~{ } 2. Симметричность. { 
}~ { 
}=> { 
}~{ 
}. 3. Транзитивность
Линейная зависимость - О1. Система { 
} наз. линейно зависимой если существуют такие числа 
, хотя бы одно из которых не равно нулю, что 
=0. О2. Если хотя бы один из векторов данной системы является линейной комбинацией других векторов, то данная система линейно зависима. Если некоторая подсистема системы векторов линейно зависима, то и вся система линейно зависима. Если система линейно независима, то любая ее подсистема линейно независима. Критерий л. зависимости: { 
} – линейно зависима тогда и только тогда, когда существует такое k {1,..,m}, что 
.
Если { 
} линейно зависима, а { 
} линейно независима, то существует k>r такое, что 
.
Теорема о замене - Если каждый из векторов линейно независимой системы е1…en линейно выражается через векторы y1…ym, то n ≤ m.
База и ранг системы векторов – базой называется любая линейно независимая подсистема, эквивалентная исходной системе. Любая ненулевая система векторов имеет базу. Для любой системы число векторов произвольной в базе одинаково. Число векторов в базе называется рангом системы.
Конечномерное пространство - Система 
- полная в V, если это система векторов такая, что любой вектор линейного пространства может быть представлен в виде линейной комбинации этих векторов или V=L(
). Если V=L(
), где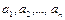 
- полная система в V, то V наз. конечномерным. В противном случае бесконечномерным.
Базис линейного пространства – базисом пространства называется полная линейно независимая система векторов. В любом ненулевом конечномерном пространстве существует базис. Для любого пространства число векторов в любом базисе одинаково. Для того, чтобы линейно независимая система была базисом, необходимо и достаточно, чтобы любая система из большего числа векторов этого пространства была линейно зависимой. Для того, чтобы полная система a1, …, an была базисом, необходимо и достаточно, чтобы либо n=1 и a1!= o, либо любая система из меньшего числа векторов не была бы полной. Пусть dimV=n и система a1, …, an — линейно независима, тогда она полна и, следовательно, является базисом. Пусть dimV=n и система a1, …, an — полная, тогда она линейно независима и, следовательно, является базисом.
Размерность линейного пространства - Число векторов в базисе конечномерного пространства V называется размерностью пространства V и обозначается dim V. Размерность нулевого пространства считается равной нулю.
Координаты векторов - Пусть e1, …, en — базис пространства V над полем F. Тогда для произвольного
вектора a из V найдутся такие числа 
из F, что a= 
. Коэффициенты разложения вектора по базису называются координатами вектора. В любом базисе координаты вектора определены единственным образом. Координаты удобно записывать в столбец, который мы будем называть координатным столбцом и обозначать [ a ] e. Координатный столбец можно рассматривать как вектор арифметического пространства Fn. Имея в виду эту интерпретацию, получаем утверждение. Для произвольных векторов a,b из V и произвольного x из F справедливо [ a + b ] e = [ a ] e + [ b ] e,
[x* a ] e = x*[ a ] e.
Изоморфизм линейных пространств – Пусть имеется V и V’ над полем F, тогда говорят, что V’ изоморфно V (V’ ~ V), если можно установить биекцию φ V на V’, сохраняющую операции, т.е φ(a+b)= φa+φb и φ(λa)= λφa.
Свойства изоморфизма.
1. Рефлексивность V ~ V
2. Симметрия V ~ V’ => V’ ~ V
3. Транзитивность V ~ V’и V’~V” => V ~ V”
4. При изоморфизме 0 соответствует 0 φ(λa)= λφa => φ0=0’
5. При изоморфизме линейно зависимая система переходит в линейно зависимую
6. При изоморфизме линейно независимая система переход в линейно независимую.
7. При изоморфизме базис переходит в базис.
8.Отношение изоморфности пространств является отношением эквивалентности.
Столбцовый и строчечный ранг системы линейных уравнений
…
