1. Вычислить точное значение определенного интеграла по формуле Ньютона-Лейбница.
2. Вычислить приближенное значение интеграла для равного количества отрезков по методу:
- Левых, правых, средних прямоугольников;
- Трапеций;
- Симпсона.
3. Вычислить абсолютные и относительные погрешности для всех методов.
4. Заполнить таблицы уk=f(xk).
| Yk | ||||||
| k | Xk | Лев. Прям. | Прав. прям. | Сред. Прям. | Трапеций | Симпсона |
| - | - | |||||
| ½ | - | - | ||||
| - | ||||||
| 1 ½ | - | - | ||||
| ... | ||||||
| n | - | - | ||||
| Интеграл |
Заполнить итоговую таблицу, в которой сравнить значения, абсолютные и относительные погрешности вычисленных интегралов.
Варианты заданий

Пример выполнения


Решение.
Вычислим интеграл в Mathcad.
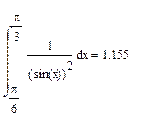
Составим программу для вычисления интеграла.
unit integr;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, ExtCtrls;
type
TForm1 = class(TForm)
Image1: TImage;
procedure Image1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
const n=50;
var
Form1: TForm1;
h,x,dx,s:real;
i:integer;
st:string;
implementation
{$R *.dfm}
procedure TForm1.Image1Click(Sender: TObject);
begin
str(n:3,st);
textout(20,5,'n='+st);
with image1.Canvas do begin
h:=3.14/3-3.14/6;
x:=3.14/6-dx;
s:=0;
dx:=h/120;
for i:=0 to 119 do
begin
x:=x+dx;
s:=s+dx*(1/sqr(sin(x)));
end;
str(s:8:4,st);
textout(20,20,' По формуле левых прямоугольников:'+st);
x:=3.14/6;
s:=0;
for i:=1 to 120 do
begin
x:=x+dx;
s:=s+dx*(1/sqr(sin(x)));
end;
str(s:8:4,st);
textout(20,35,' По формуле правых прямоугольников:'+st);
x:=3.14/6-dx;
s:=0;
for i:=0 to 119 do
begin
x:=x+dx;
s:=s+dx*((1/sqr(sin(x))+1/sqr(sin(x+dx)))/2);
end;
str(s:8:4,st);
textout(20,50,' По формуле трапеций:'+st);
x:=3.14/6;
s:=0;
for i:=1 to 120 do
begin
x:=x+dx;
s:=s+dx*(1/sqr(sin(x-dx/2)));
end;
str(s:8:4,st);
textout(20,65,'По формуле средних прямоугольников:'+st);
x:=3.14/6;
s:=0;
h:=(3.14/3-3.14/6)/2;
s:=(h/3)*(1/sqr(sin(x))+4/sqr(sin(x+h))+
1/sqr(sin(x+2*h)));
textout(20,80,'По формуле Симпсона:'+st);
end;
end;
end.
Протокол.


Содержание отчета:
1. Вывод и решение системы для определения коэффициентов полинома.
2. Таблицы.
3. Графики функций и полиномов.
4. Выводы.
Контрольные вопросы:
1. Выведите формулы прямоугольников, трапеций.
2. Что из себя представляет семейство квадратурных формул Ньютона-Котеса?
3. Что такое порядок метода? Дайте характеристику порядкам методов, применяемых в работе.
4. Как вычислить значение определенного интеграла с заданной точностью?
Литература
1. Вержбицкий В. М. Численные методы (математический анализ и обыкновенные дифференциальные уравнения). – М.: Высшая школа, 2001. – 382с.
2. Демидович Б. П., Марон И. А. Основы вычислительной математики. – М.: ФизматГИЗ, 1963. – 660с.
3. Плис А. И. Сливина Н. А. Mathcad. Математический практикум для инженеров и экономистов






