Нахождение корней нелинейных уравнений
В таблице 1 даны варианты заданий алгебраических уравнений вида f(x)=0 (уравнение 1) и трансцендентных уравнений (уравнение 2).
Таблица 1
| № варианта | Уравнение 1 | Уравнение 2 |
| х3 – 3х2 + 9х – 8=0 | x – sin x=0,25 | |
| х3 –6х – 8=0 | tg(0,58x + 0,1)=x2 | |
| х3 – 3х2 + 6х +3=0 | Öx – cos(0,387x)=0 | |
| х3 – 0,1х2 + 0,4х – 1,5=0 | tg(0,4x + 0,4)=x2 | |
| х3 – 3х2 + 9х +2=0 | lg x – 7/(2x+6)=0 | |
| х3 + х – 5=0 | tg(0,5x + 0,2)=x2 | |
| х3 +0,2х2 + 0,5х – 1,2=0 | 3x-cosx – 1=0 | |
| х3 + 3х + 1=0 | x + lg x= 0,5 | |
| х3 +0,2х2 + 0,5х – 2=0 | tg(0,5x + 0,1)=x2 | |
| х3 – 3х2 + 12х – 9 =0 | x2+4sin x = 0 | |
| х3 – 0,2х2 + 0,3х – 1,2=0 | ctg 1,05x – x2=0 | |
| х3 – 3х2 + 6х – 2=0 | tg(0,4x + 0,3)=x2 | |
| х3 – 0,1х2 + 0,4х – 1,5=0 | xlg x – 1,2=0 | |
| х3 + 3х2 + 6х – 1=0 | 1,8x2 – sin 10x – 0,1=0 | |
| х3 +0,1х2 + 0,4х – 1,2=0 | ctg x – x/4=0 | |
| х3 +4х – 6=0 | tg(0,3x + 0,4)=x2 | |
| х3 + 0,2х2 + 0,5х +0,8=0 | x2 – 20sin x + 1=0 | |
| х3 – 3х2 + 12х – 12=0 | ctg x – x/3=0 | |
| х3 – 0,2х2 + 0,3х +1,2=0 | tg(0,47x + 0,2)=x2 | |
| х3 –2х +5=0 | x2 +4sin x =0 |
Требуется:
- Построить на ЭВМ графики функций y=f(x) для локализации корней (в Excel или Mathcad)
- Выбрать любой корень в каждом из уравнений (1) и (2)
- Самостоятельно определить промежуток для уточнения корня
- Вычислить выбранные корни разными методами
- Выяснить вид сходимости в методе итераций (монотонное или двухстороннее приближение к корню).
Рекомендация: если в методе итераций получается расхождение (не выполняется условие сходимости), выразите из уравнения f(x)=0 другое Х, например:

Пример выполнения.
Решить уравнения:
 (1)
(1)
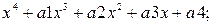 (2)
(2)
 =19,07267;
=19,07267; 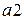 =86,59282;
=86,59282;  =-237,0059;
=-237,0059; 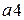 =-1697,081;
=-1697,081;
с помощью методов: комбинированного, деления пополам, секущих, итераций.
Решение.
Построим графики исходных функций для определения интервалов нахождения корней.
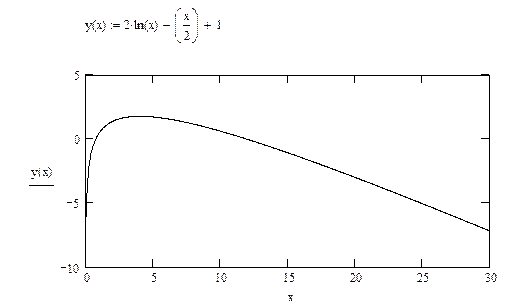

Составим программу на языке Pascal в среде Delphi 7 для нахождения корней уравнений.
unit sss111;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, ExtCtrls;
type
TForm1 = class(TForm)
Image1: TImage;
procedure Image1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
const a1=19.07267; a2=86.59282;
a3=-237.0059; a4=-1697.081;
a=10; b=12;
var
Form1: TForm1;
x,x2,l,p,f,f2:real;
i:integer;
st:string;
implementation
{$R *.dfm}
function y(k:real):real;
begin
y:=2*ln(abs(k))-(k/2)+1;
end;
function yp(k:real):real;
begin
yp:=2/abs(k)-1/2;
end;
function yn(k:real):real;
begin
yn:=k*k*k*k+a1*k*k*k+a2*
sqr(k)+a3*k+a4;
end;
function ynp(k:real):real;
begin
ynp:=4*k*k*k+3*a1*sqr(k)+2*a2*k+a3;
end;
function w(k:real):real;
begin
w:=4*ln(abs(k))+2;
end;
function wn(k:real):real;
begin
wn:=(k*k*k*k+a1*k*k*k+a2*sqr(k)+a4)/-a3;
end;
procedure TForm1.Image1Click(Sender: TObject);
begin
with Image1.Canvas do
begin
x:=a;
x2:=b;
repeat
x:=x-(y(x)/(y(x2)-y(x)))*(x2-x);
x2:=x2-y(x2)/yp(x2);
until x2=x;
str(x:30:20,st);
textout(10,10,'Комбинированный метод:'+st);
x:=a;
x2:=b;
repeat
x2:=x;
x:=w(x);
until x2=x;
str(x:30:20,st);
textout(10,25,'Метод итераций:'+st);
x:=a;
x2:=b;
repeat
l:=(x+x2)/2;
p:=y(l);
if p=0 then
begin
str(l:30:20,st);
textout(10,40,'Метод половинного деления:'+st);
i:=1;
break;
end else
f:=y(x);
f2:=y(x2);
if f*p<0 then x2:=l
else x:=l;
until x2-x<=0.00000000001;
if i<>1 then begin
str(l:30:20,st);
textout(10,40,'Метод половинного деления:'+st); end;
x2:=b;
x:=x2-y(x2)/yp(x2);
i:=0;
repeat
if frac(i/2)=0 then begin if i=0 then
p:=x2 else p:=x; end;
x:=x-y(x)*(x-p)/(y(x)-y(p));
i:=i+1;
until x-x=0;
str(l:30:20,st);
textout(10,55,'Метод секущих:'+st);
end;
end;
end.
Протокол.
Для уравнения (1) для первого и второго интервалов соответственно:


Для уравнения (2) для первого и второго интервалов соответственно:


Содержание отчета:
1. Графики функций,
2. увеличенный фрагмент графика для пояснения метода решения,
3. таблицы промежуточных значений (в таблицы заносятся изменение интервала [a;b], значения корней, функций и производных в нужных точках, абсолютные погрешности);
4. Относительные погрешности найденных корней Х и абсолютные погрешности функции (отличие от 0) в найденных точках;
5. Выводы.
Контрольные вопросы:
1. Перечислите методы отделения корней.
2. Метод половинного деления.
3. Метод хорд.
4. Метод касательных.
5. Упрощенный метод касательных.
6. Комбинированный метод хорд и касательных.
7. Метод секущих.
8. Метод итерации.
9. Что такое функция сжатия?
10. Скорость достижения требуемой точности в разных методах.
11. Надежность методов.
Лабораторная работа №2
Решение систем линейных уравнений итерационными методами
Решить СЛАУ методом итераций. Варианты заданий приведены в таблице 2:
Таблица 2
| 1). 3,5x1 - 1,7x2 + 2,8x3 = 1,7 5,7x1 + 3,3x2 + 1,3x3 = 2,1 2,1x1 + 5,8x2 + 2,8x3 = 0,8 | 2). 2,1x1 + 4,4x2 + 1,8x3 = 1,1 0,7x1 - 2,8x2 + 3,9x3 = 0,7 4,2x1 - 1,7x2 + 1,3x3 = 2,8 |
| 3). 3,1x1 + 2,8x2 + 1,9x3 = 0, 1,9x1 + 3,1x2 + 2,1x3 = 2,1 7,5x1 + 3,8x2 + 4,8x3 = 5,6 | 4). 4,1x1 + 5,7x2 + 1,2x3 = 5,8 0,8x1 + 1,1x2 - 2,8x3 = 6,7 9,1x1 - 3,6x2 + 2,8x3 = 9,8 |
| 5). 2,7x1 - 0,8x2 + 4,1x3 = 3,2 1,1x1 + 3,7x2 + 1,8x3 = 5,7 3,3x1 + 2,1x2 - 2,8x3 = 0,8 | 6). 1,9x1 + 1,1x2 + 3,8x3 = 7,8 7,6x1 + 5,8x2 - 4,7x3 = 10,1 1,8x1 - 4,1x2 + 2,1x3 = 9,7 |
| 7) 3,2x1 - 8,5x2 + 3,7x3 = 6,5 0,5x1 + 0,34x2 +3,7x3 = -0,24 4,6x1 + 2,3x2 - 1,5x3 = 4,3. | 8). 4,2x1 + 6,7x2 - 2,3x3 = 2,7; 5,4x1 - 2,3x2 + 1,4x3 = - 3,5; 3,4x1 + 2,4x2 + 7,4x3 = 1,9. |
| 9). 1,5x1 + 4,5x2 + 1,3x3 = -1,7 2,7x1 - 3,6x2 + 6,9x3 = 0,4 6,6x1 + 1,8x2 - 4,7x3 = 3,8 | 10). 3,4x1 - 3,6x2 - 7,7x3 = -2,4 5,6x1 + 2,7x2 - 1,7x3 = 1,9 -3,8x1 + 1,3x2 +3,7x3 = 1,2 |
| 11). -2,7x1 + 0,9x2 - 1,5x3 = 3,5 3,5x1 - 1,8x2 + 6,7x3 = 2,6 5,1x1 + 2,7x2 + 1,4x3 = -0,1 | 12). 0,8x1 + 7,4x2 - 0,5x3 = 6,4. 3,1x1 - 0,6x2 - 5,3x3 = -1,5; 4,5x1 - 2,5x2 + 1,4x3 = 2,5; |
| 13). 5,4x1 - 6,2x2 - 0,5x3 = 0,52 3,4x1 + 2,3x2 + 0,8x3 = -0,8 2,4x1 - 1,1x2 + 3,8x3 = 1,8 | 14). 3,8x1 + 6,7x2 + 2,2x3 = 5,2 6,4x1 + 1,3x2 - 2,7x3 = 3,8 -2,4x1 - 4,5x2 + 3,5x3 = -0,6 |
| 15). -3,3x1 + 1,1x2 + 5,8x3 = 2,3 7,8x1 + 5,3x2 + 1,8x3 = 1,8 4,5x1 + 3,3x2 - 3,8x3 = 3,4 | 16). 3,8x1 + 7,1x2 - 2,3x3 = 4,8 -2,1x1 + 3,9x2 - 6,8x3 = 3,3 8,8x1 + 1,1x2 - 2,1x3 = 5,8 |
| 17). 1,7x1 - 2,2x2 - 4,0x3 = 1,8 2,1x1 + 1,9x2 - 2,3x3 = 2,8 4,2x1 + 1,9x2 - 0,1x3 = 5,1 | 18). 2,8x1 + 3,8x2 – 8,2x3 = 4,5 2,5x1 - 7,8x2 + 3,3x3 = 7,1 6,5x1 - 1,1x2 + 4,8x3 = 6,3 |
| 19). 2,3x1 + 0,7x2 + 4,2x3 = 5,8 -2,7x1 + 2,3x2 - 2,9x3 = 6,1 9,1x1 + 4,8x2 - 5,0x3 = 7,0 | 20). 3,1x1 + 6,8x2 + 2,1x3 = 7,0 -5,0x1 - 4,8x2 + 5,3x3 = 6,1 8,2x1 + 1,8x2 + 5,1x3 = 5,8 |
Пример выполнения
Дана СЛАУ:
-93х1-18х2-74х3=5
-14х1-96х2-72х3=-79
-73х1-83х2-92х3=-73
Решить СЛАУ методом итераций.
Решение.
Приведем систему к виду:
-93х1-18х2-74х3=5
-14х1-96х2-72х3=-79
-0.8125х1+12.1843х2+18.4205х3=-7.4535
Составим программу для решения СЛАУ.
uses crt;
label m1;
var
i,j,n,k,r:integer; s:real;
a:array [1..10,1..10] of real;
xc,xn,x:array [1..10] of real;
procedure q;
begin
for i:=1 to n do
begin
s:=0;
begin
for j:=1 to n do
begin
if j=i then continue;
s:=s-a[i,j]*x[j];
end;
x[i]:=(a[i,n+1]+s)/a[i,i];
xn[i]:=x[i];
x[i]:=xc[i];
end;
end;
end;
begin
clrscr;
write('Vvedi kol-vo ur-ij:');
readln(n);
writeln('Vvedi matricj A and B:');
for i:=1 to n+1 do
begin
if i=n+1 then writeln(' B') else
write('A',i:1,' ');
end;
for i:=1 to n do
begin
gotoxy(1,i+3);
for j:=1 to n+1 do
begin
readln(a[i,j]);
gotoxy(7*j,i+3);
end;
end;
writeln;
k:=0; r:=0;
m1: k:=k+1;
repeat
begin
for i:=1 to n do
x[i]:=xc[i];
q;
for i:=1 to n do
xc[i]:=xn[i];
for i:=1 to n do
writeln('x',i:1,'=',x[i]:8:4);
writeln(k:5);
writeln('For exit press "probel"');
if readkey=#13 then
goto m1 else break;
end;
until r=0;
end.
Лабораторная работа №3






