Доказательство критерия Сильвестра основано на методе Якоби приведения квадратичной формы к каноническому виду.
| Для положительной определённости квадратичной формы необходимо и достаточно, чтобы главные миноры её матрицы были положительны. |
1. «Необходимо.» Имеется положительно определённая квадратичная форма. j-ый диагональный элемент положителен, так как k(x)>0 в том числе и для вектора со всеми нулевыми координатами, кроме j-ой. При приведении матрицы к каноническому виду не будет нужно переставлять строки, и знаки главных миноров матрицы не изменятся. А в каноническом виде диагональные элементы положительны, и миноры положительны; следовательно, (так как их знак не менялся при преобразованиях), у положительно определённой квадратичной формы в любом базисе главные миноры матрицы положительны.
2. «Достаточно.» Имеется положительность миноров. Первый минор определяет знак первого диагонального элемента в каноническом виде. Знак отношения Mi+1/Mi определяет знак i+1-ого элемента в диагональном виде. Так получим, что в каноническом виде все элементы на диагонали положительные, то есть квадратичная форма определена положительно.[1]
Ля́мбда-ма́трица (λ-матрица, матрица многочленов) — квадратная матрица, элементами которой являются многочлены над некоторым числовым полем. Если имеется некоторый элемент матрицы, который является многочленом степени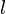 
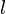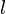, и нет элементов матрицы степени большей чем , то — степень λ-матрицы.
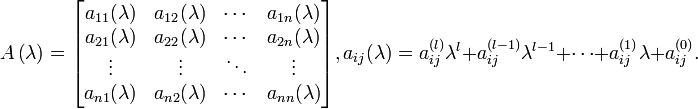
Используя обычные операции над матрицами любую λ-матрицу можно представить в виде:
В случае если определитель матрицы 
отличен от нуля, λ-матрица называется регулярной.
Аннули́рующий многочле́н для ма́трицы — многочлен, значение которого для данной квадратной матрицы равно нулевой матрице. Теорема Гамильтона-Кэли утверждает, что значение характеристического многочлена для квадратной матрицы равно нулевой матрице, а значит для каждой квадратной матрицы существует, по крайней мере, один аннулирующий многочлен степени, совпадающей с порядком матрицы.
Теоре́ма Га́мильтона — Кэ́ли — известная теорема из теории матриц, названная в честь Уильяма Гамильтона и Артура Кэли.
Теорема Гамильтона — Кэли Любая квадратная матрица удовлетворяет своему характеристическому уравнению.
Если  — квадратная матрица и  её характеристический многочлен, то  .
|
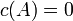Непосредственная проверка оправдывает это утверждение для матрицы порядка 2:
Характеристический многочлен
тогда
- Теорема Гамильтона — Кэли обуславливает существование аннулирующего многочлена.
- Теорема Гамильтона — Кэли эквивалентна утверждению, что характеристический многочлен делится без остатка на минимальный многочлен.
Рассмотрим присоединённую (союзную) λ-матрицу 
, где 
— единичная матрица, тогда согласно определению присоединённой матрицы
Это означает, что 
-матрица 
делится без остатка на 
, а значит, согласно следствию из теоремы Безу для -матриц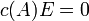 
, и следовательно .
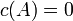