Связь между матрицами одного и того же линейного оператора в разных базисах
Если в базисе 
линейный оператор 
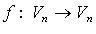имеет матрицу A, в базисе 
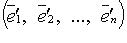- матрицу B, а S - матрица перехода от первого базиса ко второму, то
Ядро и область значений линейного оператора
Ядро оператора: 
- множество, обозначаемое Ker f:
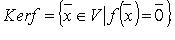
Область значений (образ) оператора - множество, обозначаемое Im f:
Множества Ker f и Im f являются подпространствами пространства V.
Ранг оператора 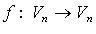(обозначение: dim Im f) - ранг матрицы A линейного оператора f,
dim Im f = rank A.
Дефектом оператора 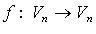называют dim Ker f,
dim Im f + dim Ker f = n.
Собственные векторы и собственные значения линейного оператора
Ненулевой вектор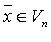 
называется собственным вектором линейного оператора 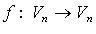, если 
(
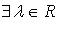для комплексного 
), такое, что 
Число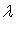 
называется собственным числом (собственным значением) оператора f, соответствующим этому собственному вектору.
Если в некотором базисе оператор f имеет матрицу А и в том же базисе вектор 
имеет координатный столбец X, то 
или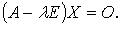 
Собственные числа 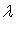линейного оператора 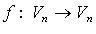- корни характеристического уравнения 
, где 
- матрица оператора f, 
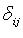- символ Кронекера.
Для каждого собственного значения 
соответствующие собственные векторы могут быть найдены из матричного уравнения 
или соответствующей ему системы линейных уравнений
Линейный оператор называется оператором простой структуры, если существует базис, состоящий из собственных векторов этого оператора. Матрица линейного оператора в этом базисе имеет вид
где 
- соответствующие собственные значения.
Квадратичные формы
Определение квадратичной формы
Квадратичная форма переменных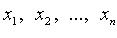 
- функция
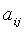- коэффициенты квадратичной формы. Без ограничения общности считают 
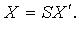тогда
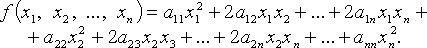
Если переменные 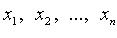принимают действительные значения и 
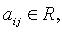квадратичная форма называется действительной.
Матричная запись квадратичной формы
Матрица
называется матрицей квадратичной формы, ее ранг - рангом квадратичной формы. Квадратичная форма называется невырожденной, если 
Главные миноры матрицы A называются главными минорами квадратичной формы.
В пространстве квадратичную форму можно записать в виде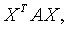 
где X - координатный столбец вектора 
В пространстве 
квадаратичную форму можно представить в виде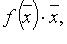 
где f - линейный самосопряженный оператор, матрица которого в некотором ортонормированном базисе равна A.
Канонический вид квадратичной формы
Квадратичная форма называется канонической, если вс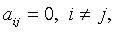е 
т. е.
Всякую квадратичную форму можно привести к каноническому виду с помощью линейных преобразований. На практике обычно применяют следующие способы.
1. Ортогональное преобразование пространства :
где 
- собственные значения матрицы A.
2. Метод Лагранжа - последовательное выделение полных квадратов. Например, если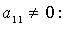 
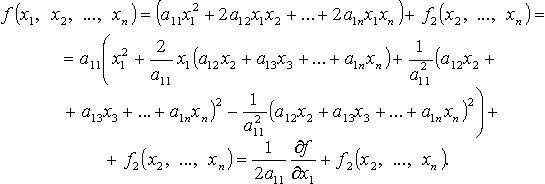
Затем подобную процедуру проделывают с квадратичной формой 
и т. д. Если в квадратичной форме все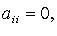 
но есть 
то после предварительного преобразования дело сводится к рассмотренной процедуре. Так, если, например,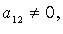 
то полагаем 
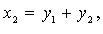
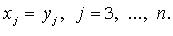
3. Метод Якоби (в случае, когда все главные миноры 
квадратичной формы отличны от нуля):
Нормальный вид квадратичной формы
Для действительной квадратичной формы
где r = rank A.
Для комплексной квадратичной формы
r = rank A.
Для действительных квадратичных форм имеет место закон инерции квадратичных форм: число положительных и число отрицательных квадратов в нормальном виде квадратичной формы не зависит от способа приведения квадратичной формы к нормальному виду с помощью невырожденных линейных преобразований.
Классификация действительных квадратичных форм
Положительно-определенные
Квадратичные формы, для которых таких, что Нормальный вид Квадратичная форма является положительно-определенной тогда и только тогда, когда все ее главные миноры положительны (критерий Сильвестра).
Отрицательно-определенные
Квадратичные формы, для которых таких, что Нормальный вид Квадратичная форма является отрицательно-определенной тогда и только тогда, когда
Положительно-полуопределенные
Квадратичные формы, для которых таких, что Нормальный вид r < n, r = rank A.
Отрицательно-полуопределенные
Квадратичные формы, для которых таких, что Нормальный вид r < n, r = rank A.
Неопределенные
Квадратичные формы, которые принимают как положительные, так и отрицательные значения. Нормальный вид: r = rank A.
Критерий Сильвестра определяет, является ли симметричная квадратная матрица положительно (отрицательно, неотрицательно) определённой.
Пусть квадратичная форма имеет в каком-то базисе матрицу
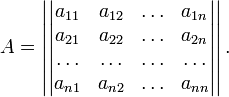
Тогда эта форма положительно определена, тогда и только тогда когда все её главные (угловые) миноры 
положительны. Форма отрицательно определена, если и только если знаки чередуются, начиная с отрицательного, причём 
. Здесь главными минорами матрицы 
называются определители вида
