Задание №1. Необходимо перемножить два беззнаковых числа (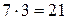
).
Решение. Для удобства возьмем длину разрядной сетки равную четырем битам, а именно:
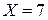- множимое;
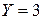- множитель;
- произведение.
Если (
) и (
) равняется четырем битам, то как было отмечено выше (
) должно быть восьмиразрядным значением, т.е длина разрядной сетки произведения в два раза больше множимого и множителя.
Алгоритм умножения младшими разрядами вперед, со сдвигом суммы (
) вправо приведен в табл. 3.1.
Таблица 3.1 - Алгоритм умножения младшими разрядами вперед, со сдвигом суммы () вправо двоичных беззнаковых чисел
| Регистр (В) множимое X | Регистр (С) множитель Y | Регистр (А) произведение Z | Счетчик тактов (Сч.Т) | Комментарии | ||||||
| 1 | ||||||||||
| множимое | ||||||||||
| 1Я СЧП | ||||||||||
| → | 1 | 1ЫЙсдвиг СЧП | ||||||||
| множимое | ||||||||||
| 2Я СЧП | ||||||||||
| → | → | 0 | 2 ОЙсдвиг СЧП | |||||||
| → | → | → | 0 | 3 ИЙсдвиг СЧП | ||||||
| → | → | → | → | 4ЫЙсдвиг СЧП | ||||||
| СТОП | ||||||||||
Задание №2. Необходимо перемножить два беззнаковых числа ().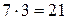
Решение. Для удобства возьмем длину разрядной сетки равную четырем битам, а именно: 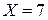- множимое, 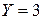- множитель, 
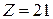- произведение.
Если () и () равняется четырем битам, то как было отмечено выше () должно быть восьмиразрядным значением, т.е длина разрядной сетки произведения в два раза больше множимого и множителя.
Алгоритм умножения старшими разрядами вперед, со сдвигом суммы () влево приведен в табл. 3.2.
Таблица 3.2 - Алгоритм умножения старшими разрядами вперед, со сдвигом суммы () влево двоичных беззнаковых чисел
| Регистр (В) множимое X | Регистр (С) множитель Y | Регистр (А) произведение Z | Счетчик тактов (Сч.Т) | Комментарии | ||||||
| 0 | ||||||||||
| 1ЫЙ сдвиг СЧП | ||||||||||
| 0 | ← | 2ОЙ сдвиг СЧП | ||||||||
| 3ИЙ сдвиг СЧП | ||||||||||
| 1 | ← | ← | 4ЫЙ сдвиг СЧП | |||||||
| 5ЫЙ сдвиг СЧП | ||||||||||
| множимое | ||||||||||
| 1Я СЧП | ||||||||||
| 1 | ← | ← | ← | 6ОЙ сдвиг СЧП | ||||||
| множимое | ||||||||||
| 2Я СЧП | ||||||||||
| СТОП | ||||||||||
Задание №3 Необходимо разделить два беззнаковых числа (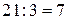
).
Решение. Для удобства возьмем длину разрядной сетки равную четырем битам, а именно: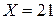 
- делимое; 
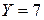- делитель; 
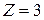- частное.
Если () и () равняется четырем битам, то как было отмечено выше () должно быть восьмиразрядным значением, т.е длина разрядной сетки делимого в два раза больше делителя и частного. Алгоритм деления приведен в табл. 3.3.
Таблица 3.3 - Алгоритм деление целых двоичных беззнаковых чисел методом с восстановлением остатка.
| Регистр (В) делимое X | Регистр (С) делитель Y | Регистр (А) частное Z | Счетчик тактов (Сч.Т) | |||||||||||||||||
| ←0 | ←0 | ←1 | ←1 | |||||||||||||||||
| 3п. | 2п. | 1п. | 0п. | |||||||||||||||||
| <0 | 03п. | |||||||||||||||||||
| ↑ | ||||||||||||||||||||
| ↑ | ||||||||||||||||||||
| ← | ↑ | |||||||||||||||||||
| ↑ | ||||||||||||||||||||
| <0→ | →0 | →0 | →0 | →0 | ↑ | |||||||||||||||
| 02п. | ||||||||||||||||||||
| ↑ | ||||||||||||||||||||
| ← | ← | ↑ | ||||||||||||||||||
| ↑ | ||||||||||||||||||||
| <0→ | →0 | →0 | →0 | →0 | ↑ | |||||||||||||||
| 11п. | ||||||||||||||||||||
| ↑ | ||||||||||||||||||||
| ← | ← | ← | ↑ | |||||||||||||||||
| ↑ | ||||||||||||||||||||
| >0→ | →1 | →1 | →1 | →1 | ↑ | |||||||||||||||
| ← | ← | ← | ← | 10п. | ||||||||||||||||
| ↑ | ||||||||||||||||||||
| >0→ | →1 | →1 | →1 | →1 | ↑ | |||||||||||||||
| СТОП | ||||||||||||||||||||
Задание №4 Необходимо разделить два беззнаковых числа ().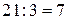
Решение. Для удобства возьмем длину разрядной сетки равную четырем битам, а именно:
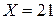- делимое;
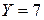- делитель;
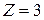- частное.
Если () и () равняется четырем битам, то как было отмечено выше () должно быть восьмиразрядным значением, т.е длина разрядной сетки делимого в два раза больше делителя и частного. Алгоритм деления приведен в табл. 3.4.
Таблица 3.4 - Алгоритм деление целых двоичных беззнаковых чисел методом без восстановлением остатка.
| Регистр (В) делимое X | Регистр (С) делитель Y | Регистр (А) частное Z | Счетчик тактов (Сч.Т) | ||||||||||||||||||||
| ←0 | ←0 | ←1 | ←1 | ||||||||||||||||||||
| 3п. | 2п. | 1п. | 0п. | ||||||||||||||||||||
| <0 | 03п. | ||||||||||||||||||||||
| ← | ↑ | ||||||||||||||||||||||
| ↑ | |||||||||||||||||||||||
| <0→ | →0 | →0 | →0 | →0 | ↑ | ||||||||||||||||||
| ← | ← | 02п. | |||||||||||||||||||||
| ↑ | |||||||||||||||||||||||
| <0 | →0 | →0 | →0 | →0 | ↑ | ||||||||||||||||||
| ← | ← | ← | 11п. | ||||||||||||||||||||
| ↑ | |||||||||||||||||||||||
| >0 | →1 | →1 | →1 | →1 | ↑ | ||||||||||||||||||
| ← | ← | ← | ← | 10п.. | |||||||||||||||||||
| ↑ | |||||||||||||||||||||||
| >0 | →1 | →1 | →1 | →1 | ↑ | ||||||||||||||||||
| СТОП | |||||||||||||||||||||||
Задание №5. Необходимо разделить два беззнаковых числа (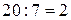
).
Решение. Для удобства возьмем длину разрядной сетки равную четырем битам, а именно:
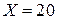- делимое;
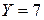- делитель;
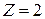- частное;
- остаток.
Если () и () равняется четырем битам, то как было отмечено выше () должно быть восьмиразрядным значением, т.е длина разрядной сетки делимого в два раза больше делителя и частного.
Как было отмечено выше последний частичный остаток должен быть больше нуля.
Если последний частичный остаток меньше нуля, его необходимо восстанавливать путем прибавления к нему делителя.
Алгоритм деления приведен в табл. 3.5.
Таблица 3.5 - Алгоритм деление целых двоичных беззнаковых чисел методом без восстановлением остатка.
| Регистр (В) делимое X | Регистр (С) делитель Y | Регистр (А) частное Z | Счетчик тактов (Сч.Т) | |||||||||||||||||
| ←0 | ←0 | ←1 | ←0 | |||||||||||||||||
| 3п. | 2п. | 1п. | 0п. | |||||||||||||||||
| <0 | 03п. | |||||||||||||||||||
| ↑ | ||||||||||||||||||||
| ↑ | ||||||||||||||||||||
| <0 | →0 | →0 | →0 | →0 | ↑ | |||||||||||||||
| 02п. | ||||||||||||||||||||
| ↑ | ||||||||||||||||||||
| <0 | →0 | →0 | →0 | →0 | ↑ | |||||||||||||||
| 11п. | ||||||||||||||||||||
| ↑ | ||||||||||||||||||||
| >0 | →1 | →1 | →1 | →1 | ↑ | |||||||||||||||
| 00п. | ||||||||||||||||||||
| ↑ | ||||||||||||||||||||
| <0 | →0 | →0 | →0 | →0 | ↑ | |||||||||||||||
| СТОП | ||||||||||||||||||||
| Счетчик тактов равняется нулю деление окончено, но последний частичный остаток получился равен меньше нуля, поэтому необходимо выполнить коррекцию, путем прибавления к последнему частичному остатку делитель. | ||||||||||||||||||||
| - коррекция | ||||||||||||||||||||
| >0 - истинный остаток. | ||||||||||||||||||||
