Задание
Определение скорости и ускоренна точки по заданным уравнениям ее движения По заданным уравнениям движения точки М установить вид ее траектории и для момента времени t= t 1 (сек) найти положение точки на траектории, ее скорость, полное, касательное и нормальное ускорения, а также радиус кривизны траектории в соответствующей точке.
Необходимые для решения данные приведены в табл.1.
Пример выполнения задания
Исходные данные в см и сек:
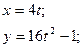 } (1)
} (1)
t 1 = 
Решение
Уравнения движения (1) являются параметрическими уравнениями траектории точки М. Чтобы получить уравнение траектории в обычной координатной форме, исключим время t из уравнений движения.
Тогда
у = х 2 - 1. (2)
Это выражение есть уравнение параболы.
Для определения скорости точки находим проекции скорости на оси координат:
ux = 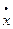 = 4 см/сек;
= 4 см/сек;
uy = 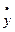 = 32 t см/сек.
= 32 t см/сек.
Модуль скорости точки
u = 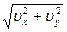 . (3)
. (3)
Аналогично проекции ускорения точки
wx =  = 0; wy =
= 0; wy = 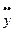 = 32 см/сек2.
= 32 см/сек2.
Модуль ускорения точки
w = 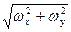 = 32 см/сек2.
= 32 см/сек2.
Координаты точки, а также ее скорость, ускорение и их проекции на координатные оси для заданного момента времени t = 1/2 сек приведены в табл.2.
Таблица 2
| Координаты, См | Скорость, см/сек | Ускорение, см/сек2 | Радиус кривизны, см | |||||||
| x | Y | ux | uy | u | wx | wy | wn | wt | w | r |
| 16,5 | 7,94 | 34,3 |
Касательное ускорение находим путем дифференцирования модуля скорости (З):
wt = 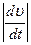 ;
;
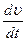 =
= 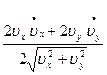 =
=  .
.
При t = 1/2 сек
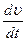 =
= 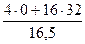 = 31 см/сек2
= 31 см/сек2
Следовательно, модуль касательного ускорения
wt = 31 см/сек 2.
Знак «+» при 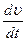 показывает, что движение точки ускоренное и, следовательно, направления
показывает, что движение точки ускоренное и, следовательно, направления 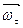 и
и 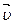 совпадают.
совпадают.
Нормальное ускорение точки в данный момент времени
wn = 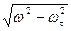 =
= 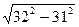 = 7,94 см/сек 2
= 7,94 см/сек 2
Радиус кривизны траектории в той точке, где при t = 1/2 сек находится в точке М,
r = 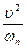 =
= 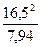 = 34,3 см.
= 34,3 см.
Полученные значения wt и wn и r также приведены в таблице.
Пользуясь уравнением (2), вычерчиваем траекторию (рис.1) и показываем на ней положение точки М в заданный момент времени. Вектор 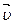 строим по составляющим
строим по составляющим 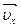 и
и 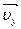 , причем этот вектор должен быть направлен по касательной к траектории точки. Вектор
, причем этот вектор должен быть направлен по касательной к траектории точки. Вектор 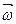 находим как по составляющим
находим как по составляющим 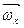 и
и 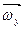 , так и по
, так и по 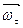 и
и 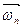 , чем контролируется правильность вычислений.
, чем контролируется правильность вычислений.

ис.1
аблица 1
| Номер варианта | Уравнения движения | t 1, сек | |
| x = x(t) см | y = y(t) см | ||
| —2 t 2+3 | — 5 t | ½ | |
4 cos2 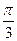 t + 2 t + 2
| 4 sin2 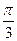 t t
| ||
-cos 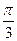 t 2 + 3 t 2 + 3
| sin 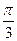 t 2 - 1 t 2 - 1
| ||
| 4 t + 4 | - 
| ||
2sin 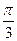 t t
| — 3 cos 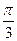 t + 4 t + 4
| ||
| 3 t 2 + 2 | —4 t | ½ | |
| Зt2 - t + 1 | 5 t 2 - 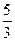 t - 2 t - 2
| ||
7 sin 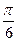 t 2 + 3 t 2 + 3
| 2 — 7 cos 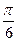 t 2 t 2
| ||
- 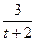
| 3 t + 6 | ||
— 4 cos 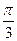 t t
| —2sin 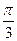 t — 3 t — 3
| ||
| — 4 t 2 + 1 | - 3 t | ½ | |
5 sin2 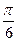 t t
| — 5 cos2 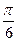 t— 3 t— 3
| ||
5 cos 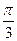 t 2 t 2
| — 5 sin 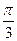 t 2 t 2
| ||
| -2 t - 2 | 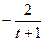
| ||
4cos 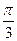 t t
| —3sin 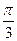 t t
| ||
| 3t | 4 t 2 + 1 | ½ | |
7 sin2 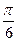 t — 5 t — 5
| — 7 cos2 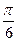 t t
| ||
1 + 3 cos 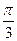 t 2 t 2
| 3 sin 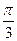 t 2 + 3 t 2 + 3
| ||
| — 5t2 — 4 | 3 t | ||
| 2 — 3 t — 6 t2 | 3 - 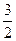 t - 3 t 2 t - 3 t 2
| ||
6 sin 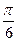 t 2 — 2 t 2 — 2
| 6 cos 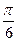 t 2 + 3 t 2 + 3
| ||
| 22. | 7 t 2—3 | 5 t | 
|
| 3 — 3 t 2 + t | 4 - 5 t 2 + 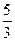 t t
| ||
— 4 cos 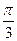 t — 1 t — 1
| — 4 sin 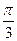 t t
| ||
| —6 t | — 2 t 2 — 4 | ||
8 cos2 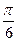 t + 2 t + 2
| — 8 sin2 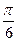 t — 7 t — 7
| ||
— 3 - 9 sin 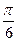 t 2 t 2
| —9cos 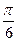 t 2 + 5 t 2 + 5
| ||
| — 4 t 2 + 1 | —З t | ||
5 t 2 + 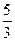 t - 3 t - 3
| 3 t 2 + t + 3 | ||
2 cos 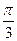 t 2 — 2 t 2 — 2
| - 2 sin  t 2 + 3 t 2 + 3
|
СПИСОК ЛИТЕРАТУРЫ
- Сборник заданий для курсовых работ по теоретической механики. Под ред. проф. А.А. Яблонского. Учеб. пособие для втузов. М., «Высшая школа», 1972.- 432 с.
- Бать М. И. И др. Теоретическая механика в примерах и задачах. М., «Политехника», 1995. – 670 с.
- Мещерский И. В. Задачи по теоретической механики. М.: «Лань», 2001.- 448 с.
- Тарг С. М. Краткий курс теоретической механики: Учебник для втузов. – 12 изд., стер. – М.: Высшая школа, 2002. – 416 с.
- Федута А. А., Чигарёв А. В., Чигарёв Ю. В. Теоретическая механика и методы математики: - Уч. пособие, - Минск.: УП «Технопринт», 2000. – 504 с.
- Яблонский А. А., Никифорова В. А. Курс теоретической механики. М.: «Лань», 2001. – 768 с.
- Цывильский В. Л. Теоретическая механика. М., «Высшая школа» 2001. – 319 с.
Игорь Павлович Карначев
Методические указания и расчетно-графические задания по курсу теоретической механики для студентов-заочников
Учебно-методическое пособие
ЛР № 040110 от 10.11.96
Подписано в печать 01.11.2002
Формат 60х84 1/16. Бумага офсетная
Офсетная печать 3,1 уч.-изд.л.
Тираж 100 экз. Изд. №
Издательство Петрозаводского
Государственного университета
Петрозаводск, пр. Ленина, 33
Отпечатано подразделением оперативной
полиграфии Кольского филиала ПетрГУ
Апатиты, ул.Космонавтов. 3






