Как известно, любую плоскую систему сил можно привести к главному вектору 
и главному моменту 
.
Если же система сил уравновешена (тело, находящееся под действием такой системы сил, либо неподвижно, либо равномерно вращается вокруг неподвижной оси, либо находится в равномерном и прямолинейном поступательном движении), то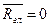 
и 
. Эти равенства выражают два необходимых и достаточных условия равновесия любой системы сил. Однако для различных систем сил на плоскости она носит свой аналитический вид.
1.1 Для произвольной плоской системы сил из этих двух условий непосредственно получаем три уравнения равновесия:
(1.1)
Первое и второе выражения – уравнения проекций – образуются из условия 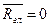; третье выражение – уравнение моментов – из условия .
1.2 Если на тело действует система параллельных сил, то уравнений равновесия получится только два: уравнение проекций на ось, параллельную силам, и уравнение моментов
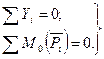(1.2)
При решении некоторых задач одно или оба уравнения проекций целесообразно заменить уравнениями моментов относительно каких-либо точек, т.е. заменить систему уравнений равновесия можно представить в таком виде:
(1.3)
или
(1.4)
В первом случае линия, проходящая через точки А и В, не перпендикулярна к оси х. Во втором же случае центры моментов А, В и С не лежат на одной прямой линии.
1.3 Для равновесия сходящихся сил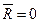 
, и следовательно, система сил уравновешена. Если построить векторный (силовой) многоугольник (рис. 1), то увидим, что он замкнется, т.е. геометрическое условие равновесия системы сходящихся сил:
(1.5)
Из геометрического условия следует аналитическое условие равновесия, выражающееся двумя уравнениями:
и 
(1.6)
При решении задач на равновесие системы сходящихся сил можно использовать три метода: графический, графо-аналитический и аналитический (метод проекций).
Необходимо учитывать, что если рассматривается равновесие плоской системы сходящихся сил, приложенных к одному телу, число неизвестных величин не должно превышать двух (условие статической определимости рис.1.)
Векторный (силовой) многоугольник задачи с плоской системой сходящихся сил):
1. неизвестна одна сила, т. е. ее модуль и направление;
2. неизвестны направления двух сил данной системы;
3. неизвестны модуль одной силы и направление другой;
4. неизвестны модули двух сил.
При графическом методе решения во всех четырех случаях можно построить замкнутый силовой многоугольник и найти в нем неизвестные величины.
Графо-аналитический метод целесообразно применять в тех случаях, когда рассматривается равновесие трех сил. При этом по условию задачи в произвольном масштабе строится замкнутых треугольник, который затем решается на основе геометрических либо тригонометрических соотношений.
Метод проекций целесообразно применять для решения задач с числом сил больше трех.
При решении задач на равновесие плоской системы сходящихся сил рекомендуется придерживаться такой общей для всех систем схемы:
1. выделить тело или точку, равновесие которой рассматривается в данной задаче, и изобразить их на рисунке;
2. выяснить, какие нагрузки действуют на тело (точку), и также изобразить их на рисунке;
3. освободить выделенное тело (точку) от связей и заменить их действие реакциями, которые надо изобразить на том же рисунке;
4. на основе полученной схемы сил построить замкнутый силовой треугольник (если рассматривается равновесие трех сил) или составить уравнения равновесия, причем при составлении уравнений проекций оси целесообразно расположить так, чтобы их направления были параллельны или перпендикулярны к искомым силам (оси проекций также показываются на рисунке);
5. после решения уравнений равновесия полученные результаты необходимо проверить либо при помощи неиспользованных уравнений или соотношений, либо путем решения задачи другим способом.
В задачах, решаемых при помощи уравнений равновесия, обычно рассматриваются тела, находящиеся в состоянии покоя, тогда система сил, действующих на это тело, уравновешена.
рис.2 рис.3
Силы, действующие на тело, делятся на две группы. Одна группа сил называется нагрузками (активные силы), вторая группа сил называется реакциями связей (пассивные силы).
Нагрузки, как правило, бывают заданы. Они имеют числовое значение, точку приложения к телу и направление их действия.
В рассматриваемых в статике задачах используются лишь три разновидности нагрузок: сосредоточенные силы, равномерно распределенные силы и пары сил (статические моменты).
Сосредоточенными называются силы, приложенные к точке тела. Если, например, на тело действуют нагрузки Р1 и Р2, как показано на рис. 2, а, действия этих нагрузок можно считать приложенными соответственно к точкам А и В тела и на расчетных схемах изобразить так, как это выполнено на рис. 2, б.
Равномерно распределенные нагрузки, например кирпичная кладка (рис. 3, а), или собственный вес однородного тела (бруса, балки) постоянного поперечного сечения по всей его длине задается при помощи двух параметров – интенсивности q и длины l, на протяжении которых они действуют. На расчетных схемах эти нагрузки изображаются так, как показано на рис. 3, б.
рис.4 рис.5
Пара сил (сосредоточенный момент), например, может быть образована двумя одинаковыми грузами Р, действующими на тело так, как показано на рис. 4, а. Условное изображение пары сил, действующей на тело, показано на рис. 4, б.
Очень часто в каком-либо месте тела возникает совместное действие сосредоточенной силы и момента. Пусть, например, груз Q подвешен на конце груза, жестко заделанного другим концом в каком-либо теле (рис. 5, б), то получим в ней совместное действие сосредоточенной силы и момента (рис.5, в).
Как правило, в задачах по статике реакции связей – искомые величины. Для каждой искомой реакции связи обычно необходимо знать ее направление и числовое значение (модуль).
Направления реакций идеальных связей – связей без трения – определяют в зависимости от вида связи по следующим правилам.
1) При свободном опирании тела на связь реакция связи направлена от связи к телу перпендикулярно либо к поверхности тела (
, 
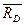; рис. 6), либо к поверхности связи (
, 
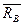; рис. 6), либо к общей касательной обеих поверхностей (
; рис. 6).
Во всех этих случаях связь препятствует движению тела в одном направлении – перпендикулярном к опорной поверхности.
2) Если связями являются нити, цепи, тросы (гибкая связь), то они препятствуют движению тела только будучи натянутыми. Поэтому реакции нитей, цепей, тросов всегда направлены вдоль их самих в сторону от тела к связи (
, 
, 
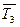; рис. 7).
3) 
Если связь тела с какой-либо опорной поверхностью осуществляется при помощи подвижного шарнира (рис. 8), то его реакция направлена перпендикулярно к опорной поверхности. Таким образом, подвижный шарнир (т. е. шарнир, ось которого может передвигаться вдоль опорной поверхности) представляет собой конструктивный вариант свободного опирания.
4) Если соединение тела со связью осуществляется при помощи неподвижного шарнира (рис. 9), то определить непосредственно направление реакции нельзя, за исключением тех частных случаев, которые описаны ниже.
Шарнирное соединение препятствует поступательному перемещению тела во всех направлениях в плоскости, перпендикулярной к оси рис.6
шарнира. Направление реакции неподвижного шарнира может быть любым в зависимости от направления действия остальных сил. Потому сначала определяют две взаимно перпендикулярные составляющие 
и 
(или 
и 
) реакции шарнира, а затем, если нужно, по правилу параллелограмма лил треугольника можно определить как модуль, так и направление полной реакции (или ).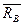
рис.7 рис.8
Направление реакции неподвижного шарнира сразу непосредственно определяют в двух случаях:
а) если, кроме реакции шарнира, все остальные силы (нагрузки и реакция другой связи) образуют систему параллельных сил, то реакция неподвижного шарнира также параллельна всем силам;
б) если, кроме реакции шарнира, на тело действуют еще только две непараллельные силы, то линия действия реакции неподвижного шарнира проходит через ось шарнира и точку пересечения двух других сил.
5) Движение тела может быть ограничено жесткой заделкой в какой-либо опоре (рис. 10). В этом случае даже одна жесткая заделка обеспечивает равновесие тела при любых нагрузках.
Так же как и неподвижный шарнир, жесткая заделка препятствует поступательному перемещению тела. Поэтому направление ее реакции заранее определить нельзя и сначала определяют составляющие 
и 
. Кроме того, жесткая заделка препятствует повороту тела в плоскости действия сил, поэтому, кроме силы реакции, на тело действует еще момент заделки 
, уравновешивающий стремление нагрузок повернуть тело (вывернуть тело из заделки).
рис.9 рис.10
Таким образом, если опорой тела является жесткая заделка, то со стороны последней на тело действуют реакция заделки, которую можно заменить двумя взаимно перпендикулярными составляющими, и момент заделки.
6) Иногда тело удерживается в равновесии при помощи жестких стержней, шарнирно соединенных с телом и с опорами (рис. 11). В отличие от гибкой связи такие стержни могут испытывать не только растяжение, но и сжатие.
рис.11
Возможны и такие случаи, когда нельзя заранее установить, какие стержни растянуты, а какие сжаты. Поэтому при составлении уравнений равновесия исходят из того, что все стержни растянуты. Если же некоторые стержни окажутся в действительности сжатыми, то в результате решения числовые значения реакций таких стержней получатся отрицательными.
Расчетно-графическое задание №1
Определение реакций опор составной конструкции (система сочлененных тел)
Найти реакции опор и давление в промежуточном шарнире составной конструкции. Схемы конструкций представлены на рисунках, размеры в (м), нагрузка в табл.1
Пример выполнения задания:
Дано: схема конструкции (рис. 1); Р1 = 10 кн; Р2 = 12 кн; М =25 кнм; q = 2 кн/м; a = 60º.
Определить реакции опор и давление в промежуточном шарнире.
Решение:
Сначала рассмотрим систему уравновешивающихся сил, приложенных ко всей конструкции (рис.2), что позволит определить вертикальные составляющие реакции опор А и В. Для упрощения вычисления момента силы 
раскладываем ее на составляющие по осям 
и 
: 
= P 1 cosa = 10 • 0,5 = 5 кн;
= Р 1 sina = 10 • 0,866 = 8,66 кн.
Рис. 1
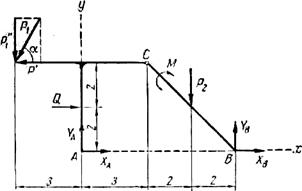
Рис.2
Уравнения равновесия имеют вид
S Мi А = 0; • 4 + • 3 - Q • 2 - М – P 2 • 5 + Y B • 7= 0, (1)
где Q = L • q = 4 • 2 = 8 кн;
S Yi = 0; - + Y A - P 2 + Y B = 0; (2)
S Xi = 0; Х A + Х B - + Q = 0. (3)
Из уравнения (1)
Y B = 
= 
= 7,86 кн.
Из уравнения (2)
Y A = + Р 2 — Y B = 8,66 + 12 — 7,86 = 12,8 кн.
Уравнение (3), содержащее два неизвестных, не позволяет определить их числовые значения.
Рассмотрим теперь систему уравновешивающихся сил, приложенных к правой части конструкции (рис. 3).
Рис.3
S МiC = 0; - M -P 2 • 2 + X B • 4 = 0; (4)
S Xi = 0; X B + X C = 0; (5)
S Yi = 0; Y C - P 2 + Y B = 0. (6)
Из уравнения (4)
X B = 
= 4,39 кн.
Из уравнения (5)
Х С = — Х В = —4,39 кн.
Из уравнения (6)
Y C = P 2 - Y B = 12 — 7,86 = 4,14 кн.
Из уравнения (3)
ХА = — Х В + — Q = —4,39 + 5 — 8 = —7,39 кн.
Для проверки правильности решения задачи убедимся в том, что соблюдается уравнение равновесия для сил, приложенных ко всей конструкции (см. рис. 2):
S MiB = 0; • 4 + • 10 - Q • 2 - Y A • 7 - М + Р 2 • 2 =
= 5 • 4 + 8,66 • 10 — 8 • 2—12, 8 • 7 — 25 + 12 • 2 = 130,6 — 130,6=0.
Результаты расчета сведем в таблицу.
| Силы, кн | |||||
| Х А | Y A | X B | Y B | X C | Y C |
| -7,39 | 12,8 | 4,39 | 7,86 | -4,39 | 4,14 |
аблица 1
| Номер варианта | Р1 | Р2 | М,кнм | q, кн/м | |||
| кн | |||||||
| 6,0 | — | 25,0 | 0,8 | ||||
| 5,0 | 8,0 | 26,0 | — | ||||
| 8,0 | 10,0 | 33,0 | 1,1 | ||||
| 10,0 | — | 25,0 | 1,3 | ||||
| 12,0 | — | 27,0 | 1,0 | ||||
| 14,0 | 12,0 | — | 0,9 | ||||
| 16,0 | 8,0 | 18,0 | 1,4 | ||||
| 12,0 | 6,0 | 20,0 | 1,0 | ||||
| 14,0 | — | 28,0 | 1,4 | ||||
| 8,0 | — | 26,0 | 0,9 | ||||
| 15,0 | 10,0 | 29,0 | 1,0 | ||||
| 15,0 | 8,0 | 28,0 | 1,5 | ||||
| 7,0 | 6,0 | 15,0 | 1,1 | ||||
| 5,0 | — | 30,0 | 0,9 | ||||
| 6,0 | 10,0 | 24,0 | 1,5 | ||||
| 8,0 | 11,0 | 31,0 | 0,8 | ||||
| 9,0 | 15,0 | 26,0 | 1,1 | ||||
| 7,0 | 16,0 | 27,0 | 0,8 | ||||
| 6,0 | 18,0 | 35,0 | 1,4 | ||||
| 7,0 | 16,0 | 32,0 | 0,8 | ||||
| 8,0 | 17,0 | 30,0 | 1,2 | ||||
| 5,0 | 6,0 | 34,0 | 1,5 | ||||
| 14,0 | 10,0 | 36,0 | 1,2 | ||||
| 10,0 | 13,0 | 28,0 | 1,3 | ||||
| 11,0 | 10,0 | 33,0 | 1,0 | ||||
| 15,0 | 15,0 | 18,0 | 1,4 | ||||
| 11,0 | 14,0 | 36,0 | 1,5 | ||||
| 12,0 | 12,0 | 30,0 | 1,1 | ||||
| 10,0 | 9,0 | 35,0 | 1,3 | ||||
| 9,0 | 10,0 | 29,0 | 1,5 | ||||
ентр тяжести тела.
Центр тяжести – точка, через которую проходит линия действия равнодействующей элементарных сил тяжести. Он обладает свойством центра параллельных сил. Поэтому формулы для определения положения центра тяжести различных тел имеют вид:
(2.1)
Если тело, центр тяжести которого нужно определить, можно отождествить с фигурой, составленной из линий (например, замкнутый или незамкнутый контур, изготовленный из проволоки, как на рис. 12), то вес 
каждого отрезка 
можно представить в виде произведения:
,
где d – постоянный для всей фигуры вес единицы длины материала.
рис.12 рис.13
После подстановки в формулы (2.1) вместо их значений 
постоянный множитель 
в каждом слагаемом числителя и знаменателя можно вынести за скобки (за знак суммы) и сократить. Таким образом, формулы для определения координат центра тяжести фигуры, составленной из отрезков линий, примут вид:
(2.2)
Если тело имеет вид фигуры, составленной из расположенных различным образом плоскостей или кривых поверхностей (рис. 13), то вес каждой плоскости (поверхности) можно представить так:
,
где 
– площади каждой поверхности, а 
– вес единицы площади фигуры.
После подстановки этого значения в формулы (2.1) получаем формулы координат центра тяжести фигуры, составленной из площадей:
(2.3)
Если же однородное тело можно разделить на простые части определенной геометрической формы (рис. 14), то вес каждой части 
, где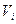 
– объем каждой части, а 
– вес единицы объема тела.
После подстановки значений в формулы (2.1) получаем формулы для определения координат центра тяжести тела, составленного из однородных объемов:
(2.4)
При решении некоторых задач на определение положения центра тяжести тел иногда необходимо знать, где расположен центр тяжести дуги окружности, кругового сектора или треугольника.
Если известен радиус дуги 
и центральный угол 
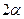, стягиваемый дугой и выраженный в радианах, то положение центра тяжести С (рис. 15, а) относительно центра дуги О определится формулой
. (2.5)
Если же задана хорда (
) дуги, то в формуле (2.5) можно произвести замену
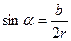
и тогда
. (2.5а)
В частном случае для полуокружности обе формулы примут вид (рис. 184, б)
. (2.5б)
Положение центра тяжести кругового сектора, если задан его радиус (рис. 15, в), определяется при помощи формулы
. (2.6)
Если же задана хорда сектора, то 
. (2.6а)
|
|
рис.14 рис.15
В частном случае для полукруга обе последние формулы примут вид (рис. 15, г)
. (2.6-б)
Центр тяжести площади любого треугольника расположен от любой стороны на расстоянии, равном одной трети соответствующей высоты.
У прямоугольного треугольника центр тяжести находится на пересечении перпендикуляров, восставленных к катетам из точек, расположенных на расстоянии одной трети длины катетов, считая от вершины прямого угла (рис. 16).
При решении задач на определение положения центра тяжести любого однородного тела, составленного либо из тонких стержней (линий), либо из пластинок (площадей), либо из объемов, целесообразно придерживаться следующего порядка:
1) 
выполнить рисунок тела, положение центра тяжести которого нужно определить в масштабе;
2) разбить тело на составные части (отрезки линий или площади, или объемы), положение центров тяжести которых определяется исходя из известных размеров по чертежам;
3) определить длины (площади, объемы) составных частей;
4) выбрать расположение осей координат или оно уже известно;
5) определить координаты центров тяжести составных частей;
6) найденные значения подставить в соответствующие формулы и вычислить координаты центра тяжести всего тела;
7) по найденным координатам указать на рисунке положение рис.16
8) центра тяжести для всего тела.
Расчетно-графическое задание №2
Определение положения центра тяжести плоского тела
Найти координаты центра тяжести плоской фигуры, размеры — в сантиметрах.
Пример выполнения задания:
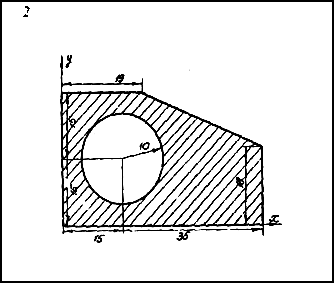
Определить координаты центра тяжести плоской фигуры, показанной на рис. 1.
Решение
ис.1
Координаты центра тяжести площади определяем по формулам:
xC = 
; y C = 
. (1)
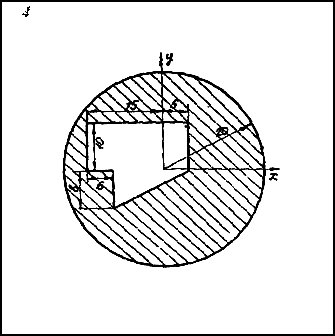
Чтобы воспользоваться этими формулами, площадь фигуры делим на отдельные части, положения центров тяжести которых известны. В данном случае такими частями являются: прямоугольник, треугольник и половина круга (рис.2). Площадь половины круга, вырезанную из площади прямоугольника, считаем отрицательной.
Имеем:
площадь прямоугольника
F 1 = 40 • 30 = 1200 см2,
площадь треугольника
F 2 = 
= 1000 см2;
площадь половины круга
F 3 = 
= 200 p = 628 см 2
Рис.2
Центры тяжести рассматриваемых частей сечения имеют следующие координаты:
для прямоугольника
х 1 = 15 см; у 1 = 20 см;
для треугольника
x 2 = 30 + 
= 46,7 см; y 2 = 
= 13,3 см;
для половины круга
х 3 = 
= 
= 8,5 см; y 3 = 20 см.
Для вычисления координат центра тяжести плоской фигуры составляем таблицу.
| Номер элемента | Fi,см 2 | xi,см | yi,см | Siy = Fi xi, см 3 | Six = Fi yi, см 3 |
| -628 | 15,0 46,7 8,5 | 20,0 13,3 20,0 | -5338 | -12560 | |
| S | -- | -- |
По формулам (1) вычисляем координаты центра тяжести плоской фигуры:
x C = 
=37,8 см; y C = 
=15,7 см.
Центр тяжести площади указан на рис. 2.
 |
 |
