восьмиричной и шестнадцатиричной системах счисления
Алгоритм поразрядного сложения:С=А+В.
где сi ‑ цифра і-го разряда результата;
рі+1 ‑ перенос в i +1 разряд.
Алгоритм поразрядного вычитания: R=А-В.
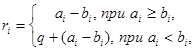
где rі ‑ цифра і-го разряда результата;
zі+1 ‑заем из i+1 разряда.
Алгоритм порaзрядного умножения: S=А*В.
где s і ‑ цифра і-го разряда результата;
рі+1 ‑ перенос в i+1 разряд.
В разных системах счисления могут выполняться все 4 арифметические операции: сложение, вычитание, умножение и деление.
ДВОИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ. Для выполнения простейших операций – сложение и вычитание ‑ удобно пользоваться таблицей сложения:
| + | ||
Пример: 0 + 1 = (нулевая строка и первый столбец при пересечении дают 1). Аналогично, 1 + 0 = 1; 1 + 1 = 10.
Операция вычитания предполагает обратную процедуру.
Примеры:
11011 1101001 10101011,011 110,0111
+ 10111 – 110111 + 11010100,101 – 11,1111
10010 110010 110000000,000 10,1000
ВОСЬМИРИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ. Таблица для сложения и вычитания чисел в восьмиричной системе счисления.
Таблица 3
| + | ||||||||
Таблица для сложения и вычитания чисел в восьмиричной системе счисления применяется следующим образом:
2 + 6 = 10; 11-7 = 2
Примеры:
723 126 72165,23 11610,23 19951026
+ 334 – 27 + 37734,54 – 2716,67 – 19951022
1257 77 132121,77 6671,34 4
ШЕСТНАДЦАТИРИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ. Таблица для сложения и вычитания чисел в шестнадцатиричной системе счисления используется также, как и таблицы для двоичной и восьмиричной систем счисления.
Таблица 4
0 1 2 3 4 5 6 7 8 9 A B C D E F
0 0 1 2 3 4 5 6 7 8 9 A B C D E F
1 1 2 3 4 5 6 7 8 9 A B C D E F 10
2 2 3 4 5 6 7 8 9 A B C D E F 10 11
3 3 4 5 6 7 8 9 A B C D E F 10 11 12
4 4 5 6 7 8 9 A B C D E F 10 11 12 13
5 5 6 7 8 9 A B C D E F 10 11 12 13 14
6 6 7 8 9 A B C D E F 10 11 12 13 14 15
7 7 8 9 A B C D E F 10 11 12 13 14 15 16
8 8 9 A B C D E F 10 11 12 13 14 15 16 17
9 9 A B C D E F 10 11 12 13 14 15 16 17 18
A A B C D E F 10 11 12 13 14 15 16 17 18 19
B B C D E F 10 11 12 13 14 15 16 17 18 19 1A
C C D E F 10 11 12 13 14 15 16 17 18 19 1A 1B
D D E F 10 11 12 13 14 15 16 17 18 19 1A 1B 1C
E E F 10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D
F F 10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D 1E
 |
Пример:
9 + В = 14 1A – F = B
Алгоритм операции деление: С=А:В.
Операция деления выполняется с использованием правил десятичного деления с помощью методов умножения и вычитания.
Сначала делаем сдвиг делителя к старшему разряду делимого на n разрядов. Потом от делимого отнимаем сдвигаемый делитель до тех пор, пока остаток будет меньше, чем сдвигаемый делитель. Цифра частного определяется количеством вычитаний сдвигаемого делителя.
Остаток сдвигается на один разряд влево и определяется следующая цифра частного. Количество разрядов целой части частного на 1 больше количества сдвигов разрядов делимого, то есть n+ 1.
Пример:
256 (10)| 2 Делитель = 002; n = 2;
- 200 1 2 8 Сдвигаемый делитель = 200;
56 Количество разрядов целой части частного = 3.
560
-400
1600
-1600
2.4. Представление чисел в ЭВМ
В зависимости от способа представления в них чисел машины делятся на машины с фиксированной запятой и машины с плавающей запятой.
В машинах с фиксированной запятой применяется естественная форма записи чисел: число представляется в виде последовательности цифр, разделенной на целую и дробную часть.
Ячейка памяти такой машины состоит из знакового разряда и цифровых разрядов. Постоянное количество числовых разрядов отведено для хранения целой части числа, остальные цифровые разряды предназначены для изображения ее целой части.
| знак | Целая часть | Дробная часть |
Название "машина с плавающей запятой (точкой)" происходит от того, что при записи чисел в ячейках запятая помещается (с помощью записи в указателе положения запятой) после любого цифрового разряда ячейки.
При этом используются числа в так называемой нормализованной форме. Числа с плавающей запятой представляются в ЭВМ по формуле:
А = М*q p,
где М ‑ мантисса;
q ‑ основание системы счисление;
р ‑ порядок числа.
Мантисса числа ограничена диапазоном
q –1 < |M| < 1.
Мантисса нормализуется таким образом, чтобы первой цифрой после запятой была значащая цифра, а не нуль. Если после вычисления мантисса имеет в старших разрядах нули, то она при нормализации сдвигается влево на количество нулевых разрядов и при этом порядок уменьшается на столько же единиц, сколько сдвигов влево было в мантиссе. Например, отобразим число А = -13,75 (10) в форме с плавающей запятой.
-13,75 (10) = -1101,11 (2) = -D,C (16) = -DC*16 1
При этом: М = -0,DC00 (16) = -0,1101 1100 0000 0000 (2)
В современных ЭВМ используется не порядок, а характеристика (Х), которая более порядка на 64 единицы. Таким образом, характеристика числа будет:
Х = р+64 (10) =р+40 (16) = р+01000001 (2)
[A] п.к. = 1.11011100*101000001
знак мантиссы
31 0
Х = р+40 (16) Мантисса от 3 до 7 байт
Характеристика
Рис.1. Формат чисел с плавающей запятой
Диапазон порядка находится от –64 к +63: -64 (10) < p < 63 (10), а диапазон характеристики — 0 < X < 127 (10)
Рассмотрим пример записи числа [A] п.к. = 1.11011100*101000001 в регистр ЭВМ с плавающей запятой (рис.2.).
 1
| ... |
Х М
Рис. 2. Пример записи числа с плавающей запятой
где 0,1£ m <1,
m - мантисса,
p - показатель степени.
| знак | Цифровые разряды мантиссы | Знак порядка | Порядок |
КОДИРОВАНИЕ ЧИСЕЛ. Для записи и хранения числовой информации в памяти ЭВМ используются не сами числа, а их коды.
Кодом числа называется условное изображение числа в машине для выполнения арифметических операций. Двоичные числа могут быть представлены в прямом, обратном и дополнительных кодах.
Для кодирования знака числа используется один двоичный разряд, в котором знак "+" изображается цифрой 0; знак "-" изображается цифрой 1. Поскольку положительные числа в различных кодах одинаковы, то специальное кодирование относится только к отрицательным числам.
Отрицательные числа в прямом, обратном и дополнительном кодах имеют различное изображение, но знак числа "-" кодируется как "1" для всех видов кодов.
Отрицательное число в прямом коде сохраняет свое изображение, в обратном коде разряды нулей заменяются единицами, а единицы - нулями. Дополнительный код отрицательного числа соответствует обратному коду числа с прибавлением единицы к младшему разряду.
Прямой код используется при вводе и выводе чисел, а также при сохранении чисел в памяти ЭВМ.
В прямом коде все разряды числа остаются неизменными. Например,
А (2) =1101 [A]п.к. = 0.1101; А (2) = - 0,1101 [A]п.к.= 1.1101
Прямой код используется при умножении чисел. Например,
С=А*В; А (2) =1011; B (2) = -1010;
Сначала вычисляем знаковые разряды путем сложения по модулю 2:
| Å | ||
Å ‑ обозначение операции «сложение по модулю 2».
Получаем 0+1=1. Таким образом, результат будет иметь знак в прямом коде 1, что отображает знак минус.
х 1010
+ 10110
Результат: [C] пк. = 1.1101110 (2).
С (2) = - 1101110 = - (1*26+1*25+1*23+1*22+0*20) = - (64+32+8+4+2) = - 110(10)..
Вычитание в ЭВМ выполняется как операция сложения в обратном или дополнительном коде.
Если число А>0, то обратный код пишется как прямой: [A] обр.к. = [A] пк.
Если число А<0, то все разряды числа, кроме знакового, инвертируются. Операция инверсии выполняется по формуле:
b и= (q - 1) – b и.
Нуль в обратном коде в двоичной системе счисления имеет два изображения: “+0” = 0.00...0; “-0” = 1.11...1. В десятичной системе счисления нуль имеет такие изображения: “+0” = 0.00...0; “-0” = 9.99...9.
Переход от обратного кода к прямому осуществляется как и при переходе от прямого к обратному с помощью операции инверсии.
Рассмотрим пример сложения чисел с разными знаками в обратном коде в двоичной и десятичной системах счисления. С = А+(-В):
В двоичной системе счисления: В десятичной системе счисления:
А (2) = 1011; [A]обр.к.= 0.1011; 0.1011 А (10) = 11; [A]обр.к.= 0.11; 0.11
В (2)= - 101; [A] обр.к. = 1.1010; +1.1010 А (10) = -5; [A]обр.к. = 9.94; +9.94
(1)0.0101 (1)0.05
+ 1 + 1
0.0110 0.06
При сложении в обратном коде перенос из старшего (знакового) разряда прибавляется к младшему разряду суммы для получения верного результата.
Если число А>0, то дополнительный код пишется как прямой:
[A] д.к. = =[A]п.к.
Если число А<0, то все разряды числа, кроме знакового, инвертируются и к младшему разряду прибавляется 1.
Пример:
А (2) = - 1010; [A]д.к.= [A]обр.к. + 0.0001 = 1.0101+0.0001 = 1.0110.
Переход от дополнительного кода к прямому осуществляется как и при переходе от прямого к дополнительному (сначала преобразуется в обратный код, а потом к этому числу добавляется 1 младшего разряда).
Рассмотрим примеры сложения чисел с разными знаками в дополнительном коде:
В двоичной системе счисления: В десятичной системе счисления:
А (2) = 1011; [A]д.к.= 0.1011; 0.1011 А (10) = 11; [A]о.к.= 0.11; 0.11
В (2)= - 101; [A] д.к. = 1.1011; +1.1011 А (10) = -5; [A]о.к. = 9.95; +9.95
(1)0.0110 (1)0.06
Результаты: А (2) = 110; А (10) = 6.
При сложении в дополнительном коде перенос из старшего (знакового) разряда отбрасывается для получения верного результата.
Переполнение разрядной сетки ведет к ошибке вычисления. Рассмотрим переполнения разрядной сетки на примерах:
1) А (2) = 1011,0111; [A]м.п.к. = 00.1011,0111
В (2) = 1101,1011; [B ]м.п.к. = 00.1101,1011
01.1001,0010
2) А (2) = - 1011,0111; [A]м. д.к. = 11.0100,1001
В (2) = - 1101,1011 [B] м.д.к. = 11.0010,0101
10.0110,1110
При сложении чисел с одинаковыми знаками при переполнении разрядной сетки знак результата становится другим, что является признаком переполнения. Для выявления в ЭВМ признака переполнения применяется модифицированный дополнительный код, в котором под знак числа отводятся два двоичных разряда. При этом знак “+” отображается как 00, а знак “-” ‑ 11. При переполнении знаки результата приобретают вид 01 (при сложении положительных чисел ‑ А>0) и 10 (при сложении отрицательных чисел ‑ А<0)
