Каждая техническая система обладает несколькими фундаментальными характеристиками. Наиболее значимые для задач управления - управляемость и наблюдаемость. Управляемость (controllability) - это характеристика системы, которая показывает, имеет ли система достаточное количество регулируемых параметров для того, что бы управлять ею требуемым образом. Система является управляемой, если можно подобрать такие управляющие воздействия, при которых система достигает заданного состояния. Если некоторая переменная состояния не зависит от управления u(t), то отсутствует возможность требуемого изменения этой переменной с помощью произвольного управляющего воздействия за конечное время. Поэтому эта переменная состояния называется неуправляемой, и система в целом также является неуправляемой по этой переменной.
Система называется полностью управляемой по состоянию, если для произвольного начального момента времени (шага) t0 существует последовательность неограниченных управлений u(ti), i=0,1,2,..., n-1, которая переводит каждое начальное состояние y(t0) в некоторое конечное состояние y(tn) за конечное время (число шагов) tn>t0.
Система называется полностью управляемой по выходу, если для произвольного начального времени (шага) t=t0 существует последовательность неограниченных управлений u(ti), i=0,1,2,..., n-1, таких, при которых некоторое конечное значение выходной переменной y(tn) может быть достигнуто из произвольного начального состояния системы за конечное время (число шагов) tn>t0.
Аналогичные рассуждения справедливы и для дискретной модели.
Управляемость линейной системы на базе непрерывной и дискретной модели можно проверить математическими методами. Однако никакие математические методы не могут заменить понимание физической природы процесса инженером-проектировщиком. Например, бывает, что некоторые параметры плохо управляемы. В этом случае формально система управляема, однако реальный регулятор, пригодный для практического использования, создать невозможно.
Вторая характеристика системы ‑ наблюдаемость ‑ связана с измерениями и наблюдением. Позволяет ли имеющийся состав датчиков получить достаточную информацию о состоянии системы? Возможно ли косвенным образом вычислить весь текущий вектор состояния х(t), если известны текущее и предыдущее значения выходного сигнала у(t)? Понятие наблюдаемости является дуальным по отношению к управляемости. Процесс называется наблюдаемым, если каждая переменная состояния процесса обусловливает изменение некоторых выходных переменных процесса, которые могут быть измерены. Линейная цифровая система называется полностью наблюдаемой, если для некоторого времени t0 состояние x(t0) может быть определено по известным выходной y(t) и входной u(t) переменным для t0< t < tn, где tn - конечное время или шаг.
В большинстве случаев полное состояние системы не может быть измерено непосредственно. Однако, для целей управления часто важно знать полный вектор состояния х(t), даже если адекватные датчики не существуют. Например, иногда требуется "оценить" по изменениям входных и выходных сигналов те переменные состояния, которые необходимы для закона управления, но непосредственно не могут быть измерены.
При определенных условиях полный вектор состояния х(t) можно вычислить основе измерений выходов системы у(t). Обозначим вычисленный вектор состояния – x*, поскольку он может отличаться от реального.
Для вычисления неизмеряемых переменных состояния можно использовать процедуру оценки (estimator), причем как для непрерывных, так и для дискретных моделей. Рассмотрим алгоритм оценки для дискретной модели, поскольку его можно непосредственно применять в компьютерном управлении. Оценка состояния фактически является описанием технического процесса разностными уравнениями (1.15), в которые введен дополнительный член для корректировки оцениваемых переменных на основе измерений у(t)
x*[(k+1)∙h]= Ф ∙x*(k∙h)+ Г ∙u(k∙h)+ K ∙[y(k∙h)- C ∙x*(k∙h)] (1.24)
где матрицы Ф, Г определяют соответствующие коэффициенты адекватной модели процесса. Матрица К есть весовой коэффициент, определяющий качество оценки. При "отличной" оценке х* и х совпадают с достаточной точностью и последнее слагаемое в уравнении (1.24) равно нулю, так
как у = С ∙х*. Оценка будет подчиняться тому же динамическому уравнению, что и истинный вектор состояния. Поскольку x* отличается от х, последнее слагаемое, т.е. разность между реальным измерением у и его оценкой С ∙x, используется для коррекции ошибки. Работа алгоритма оценки иллюстрируется рис. 1.4, где показано, как выход модели С ∙x постоянно корректируется измеренными значениями у. Если значения К выбраны правильно, то x* сходится к действительным значениям внутренних параметров х.
В верхней части рисунка изображен технический процесс, а в нижней - процедура его оценки по всем переменным состояния, т.е. компьютерная модель на основе уравнений (1.24).
Рис. 1.6. Определение (оценка) значений внутренних переменных процесса.
Другими словами, оценка есть не что иное, как компьютерная модель технического процесса, которая регулярно корректируется на основе текущих измерений. Для проверки сходимости используется величина, которая называется оценкой погрешности (estimation error).
xe(k∙h) = x(k∙h) – x*(k∙h) (1.25)
Используя уравнение (1.15), после преобразований погрешность оценки запишем
xe[(k+1)∙h] = Ф ∙x*(k∙h)- К [y(k∙h)- C ∙x(k∙h)]=(Ф-К ∙ С) ∙x*(k∙h) (1.26)
Если К в алгоритме оценки можно выбрать так, что xe(kh) сходится достаточно быстро к нулю, то оценка является удовлетворительной. Это означает, что x*(kh) будет сходиться к x(kh) независимо от начальных условий. Более того, К можно подобрать таким образом, что погрешность будет сходиться быстрее, чем исходная аппроксимация, определяемая матрицей Ф.
Возможность выбрать К таким образом, чтобы оценка была приемлемой, зависит от наблюдаемости системы, которая определяется только матрицами Ф и С. Иначе говоря, наблюдаемость характеризует возможность получить информацию обо всех состояниях x(t) системы на основе выходных сигналов у(t). Наблюдаемость также гарантирует, что можно найти подходящую матрицу К такую, что x*(k∙h) быстро сходится к нулю. Ненаблюдаемость означает, что некоторые параметры состояния не отражены в измерениях. В общем случае управляемость и наблюдаемость линейной системы, как правило, могут определяться более сложно, с применением математических критериев.
Рассмотрим движение массивной нагрузки под действием вращающего момента Мвр, передаваемого упругим валом. Сила закручивания вала (упругий момент) пропорциональна разности между углами поворота φ1, φ2 входной и выходной части передающего вала. Дополнительно, разность скоростей на краях вала обеспечивает диссипативный момент, обусловленный демпфированием, пропорциональным разности угловых скоростей на входе и выходе упругого вала. При моменте инерции нагрузки J1 уравнения движения имеет вид
(1.27)
Введем
x1=φ1-φ2
y(t)=x2
тогда исходное уравнение запишется
(1.28)
Производные аппроксимируются конечными разностями в соответствии с (1.16) с шагом h
(1.29)
где k=0,1,2, …
Оценка имеет вид
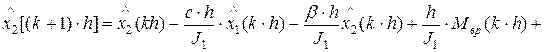(1.30)
Цель оценки ‑ вычислить x2(k∙h) на основе измерений у=x1(k∙h). Коэффициенты К1 и К2 определяют скорость приближения оценки к реальному значению. Начальные условия реальной системы зачастую неизвестны, и поэтому, в некоторых случаях, их можно считать нулевыми. После каждого шага решения, оценка приближается к реальным значениям параметров процесса. После того, как оценка достигнет действительного значения (с определенной погрешностью), то они и дальше остаются идентичными, даже если входной момент Мвр изменяется. Точность получения оценки в основном зависят от точности и адекватности модели, а так же от величины шага оценки.
Поскольку в цифровой системе управления присутствуют операции квантования, условие управляемости и наблюдаемости может зависеть от периода квантования. В общем случае, при дискретном управлении имеется ограниченное количество достижимых состояний, из-за дискретного представления информации, квантования программ по времени и конечной длины машинного слова.
