екция 4
Дискретные модели динамических систем.
При использовании в системах управления цифровой ЭВМ, сбор данных и выработка управляющих сигналов происходят только в определенные моменты времени. Ситуация принципиально не меняется при повышении скорости процессора - данные остаются дискретными выборками непрерывного сигнала.
Приведем пример формирования модели физического процесса, пригодной для компьютерного управления. В соответствии с дискретным характером модели, измеряемые данные собираются через регулярные интервалы времени. Эти интервалы не обязательно должны быть одинаковыми, однако описание дискретной динамически модели проще при постоянном интервале времени. Данный процесс называется выборкой, дискретизацией (sampling) или квантованием, величина интервала времени – периодом дискретизации (sampling time) или квантования. Будем считать, что измеряемые данные и сигналы управления остаются неизменными в течение интервала выборки.
Дискретное описание в пространстве состояний.
Нелинейный процесс, описанный уравнениями (1.11) можно аппроксимировать разностным уравнением
x[(k+1)·h]≈ x(k·h)+h∙f(x,u) (1.15)
где h - интервал выборки и k - его порядковый номер; f(x,u) производная по времени вектора состояния системы х в соответствии с уравнением (1.11). Аппроксимация справедлива, если h достаточно мал и производная функции гладкая. Линейная система с постоянными коэффициентами в дискретном виде может быть представлена следующим образом
x1[(k+1)·h]=(1+h·a11)·x1(k·h)+…+h·a1n·xn(k·h)+ h·b11·u1(k·h) +…+ h·b1r·ur(k·h)
.
. (1.16)
.
xn[(k+1)·h]=(1+h·an1)·x1(k·h)+…+h·ann·xn(k·h)+ h·bn1·u1(k·h) +…+ h·bnr·ur(k·h)
Предполагается, что сигнал управления u(t) остается постоянным между моментами выборки, т.е. система включает в себя схему удержания или выборки/хранения.
Аппроксимация конечными разностями (1.16) стремится к точному решению при малых значениях h интервала выборки. Решение уравнений дискретной модели
y (k·h)= C · x (k·h)+ D · u (k·h) (1.17)
на цифровой ЭВМ получается в последовательные моменты времени на основе решения шаг за шагом разностных уравнений.
оскольку измерения происходят периодически, то уравнение (1.16) для дискретной модели справедливо только в моменты выборки.
Дискретное описание процесса через отношение вход/выход.
В дискретных моделях, так же как и в непрерывных, часто удобно напрямую связать вход процесса w с его выходом, в особенности, когда регулятор записан в такой форме, т.е. он оперирует выходной величиной процесса для расчета управляющего сигнала. Дискретно-временной анализ проще выполнить при помощи операторов сдвига q (shift operator). Эффект от применения оператора к зависящей от времени переменной z (t) такой же, что и сдвиг по времени на интервал h – его также называют сдвигом вперед (forward shifting).
q·z(k·h)=z[(k+1)·h] (1.18)
С помощью оператора сдвига можно заменить разностные уравнения на алгебраические, которые проще преобразовывать и решать. Здесь используется принцип аналогичный преобразованию Лапласа для упрощения дифференциальных уравнений с помощью комплексной переменной.
Оператор обратного сдвига q-1 (backward shift operator) сдвигает функцию времени на один шаг назад. В общем случае оператор сдвига можно применять несколько раз
qn·z(k·h)=q·q·…q·z(k·h)=z[(k+n)·h] (1.19)
Оператор сдвига q можно применять и к вектору x(k·h), что эквивалентно использованию этого оператора к каждому его компоненту.
Если существует дискретное представление в пространстве состояний [уравнение (1.17)], то, исключив вектор х и приведя подобные члены, получим связь между входом и выходом в виде
y[(k+n)·h]+a1·y[(k+n-1)·h]+…+an·y(k·h)=b0·u[(k+n)·h]+…+bn·u(k·h) (1.20)
Применение оператора сдвига q дает более компактную запись
(qn+a1·qn-1+…+an)·y(k·h)=(b0·qn+b1·qn-1+…+bn)·u(k·h) (1.21)
Зависимость между входными и выходными переменными линейной системы можно представить передаточной функцией, определяемой как отношение изображений Лапласа входных и выходных сигналов системы. Аналогичное описание можно получить с помощью оператора сдвига q для дискретных систем. Дискретный передаточный оператор H(q) (discrete operator) определяется из уравнения (1.21) следующим образом
H(q)= 
(1.22)
Выражения в обеих частях уравнения (1.22) можно сдвинуть на n периодов назад. При использовании оператора обратного сдвига, отношение вход/выход выражается в виде
H*(q)=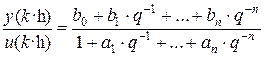 
(1.23)
В дискретном случае, как и для непрерывной передаточной функции, коэффициенты однозначно определяются из внутреннего описания в пространстве состояний.
