остроение моделей сложной формы
остроение тел по траектории
Рис1.1 Наковальня.
Рис 1.2. Пружина.
Рис 1.3. Сверло.
остроение тел по сечениям
Рис1.2.1. Корпус.
Данный корпус был испытан в аэродинамической трубе рис.1.2.2. Рабочая среда – вода. Входное давление - 
. Выходное давление 
. Температура рабочей среды Т = 400 К.
Рис1.2.2. Продувка крышки в трубе.
ормирование чертежа на основании 3D модели
Рис 2.1 Модель детали.
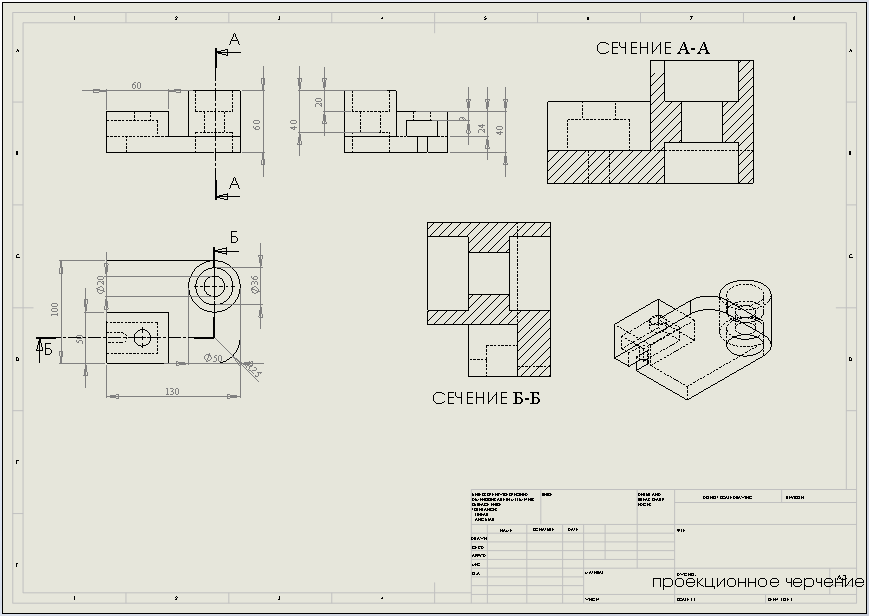
Рис 2.2. Чертёж детали рисунка 2.1.
3. Сравнительный анализ расчётов изгиба балки
Балка размерами 80х20х1мм, материал – нержавеющая сталь. Балка нагружается постепенно грузиками. Масса каждого грузика 100г, количество грузиков – 5. Балка закреплена консольно. Во время нагружения в месте закрепления возникают максимальные напряжения, максимальный игиб в точке приложения силы. В данном испытании мы испытываем два образца с разными направлениями волокон. На рисунке 3.1. представлена эпюра максимальных напряжений, на рисунке 3.2. представлена эпюра максимальных перемещений.
Рис. 3.1. Эпюра напряжений.
Рис 3.2. Эпюра перемещений.
Результаты расчётов прогиба и напряжений балки выполнены в модуле COSMOS Works. Для расчёта прогиба используется метод конечных элементов (МКЭ) рис 3.3., рис3.4.
Рис. 3.3. Напряжения, возникающие в балке при нагрузке в 1 Н (100г).
Рис. 3.4. Перемещения, возникающие в балке от нагрузки 1 Н (100г).
Так же был произведён эксперимент, в котором мы постепенно нагружали образцы и снимали результаты нагружения и разгружения балки. Так же были проведены теоретические расчёты прогиба балки по формулам:
l – длина;
P – нагрузка;
E – модуль Юнга (упругости первого рода);
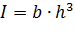– момент инерции.
Все расчёты и измерения были сведены в сводные таблицы для образца 1 таблица 3.1., для образца 2 таблица 3.2.
Таблица 3.1.
| Нагрузка | ||||||
| Y нагрузки | 0,47 | 1,07 | 1,73 | 2,35 | 3,05 | |
| Y разгрузки | 0,68 | 1,15 | 1,95 | 2,56 | 3,05 | |
| МКЭ | 0,5 | 1,02 | 1,54 | 2,01 | 2,53 | |
| Расчётный прогиб | 0,48762 | 0,97524 | 1,46286 | 1,95048 | 2,4381 |
Таблица 3.2.
| Нагрузка | ||||||
| Y нагрузки | 0,46 | 1,07 | 1,72 | 2,38 | 3,07 | |
| Y разгрузки | 0,06 | 0,67 | 1,3 | 2,6 | 3,07 | |
| МКЭ | 0,5 | 1,02 | 1,54 | 2,01 | 2,53 | |
| Расчётный прогиб | 0,48762 | 0,97524 | 1,46286 | 1,95048 | 2,4381 |
На графиках 3.5. и 3.6. представлены зависимости перемещения от нагрузки.
График 3.5. Перемещение балки образца 1.
График 3.6. Перемещение балки образца 2.
По графикам видно, что МКЭ отличается от эксперимента и от результатов полученных расчётными формулами. Это может быть связано с отличием физических свойств, так как на практике они отличаются от тех, которые заложены в базе программы (Модуль Юнга, анизотропия свойств материала).
4. Расчёт на прочность и жёсткость
Материал кольца – графит.
Материал основания – простая углеродистая сталь.
Действующий момент 
.
Коэффициент трения f = 0,1.
Наружный диаметр втулки D = 40 мм.
Внутренний диаметр втулки d = 20 мм.
Теоретическим путем была рассчитана необходимая сила зажима N.
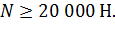
Рис. 4.1. Модель сборки.
| А |
Рис 4.2. Модель напряжения кромки А.
График 4.3. Эпюра напряжений кромки А.
| Б |
Рис. 4.4. Модель перемещений кромки Б.
График 4.5. эпюра перемещений кромки Б.
5. Тепловой расчёт
Уплотнительное кольцо из керамики установлено в консольно закрепленной трубе из нержавеющей стали.
Температура Т = 500 К.
Сначала испытывается кольцо без эксцентриситета.
Рис. 5.1. Уплотнительное кольцо без эксцентриситета
Возникающие напряжения в кольце, показаны на рисунке 5.2.
Рис. 5.2. Контактные давления в уплотнительном кольце без эксцентриситета.
С целью снижения напряжений, возникающих в уплотнительном кольце, его изготавливают с эксцентриситетом.
Рис. 5.3. Уплотнительное кольцо с эксцентриситетом.
Рис. 5.4. Контактные давления в уплотнительном кольце с эксцентриситета.
