$$ прочность
$ пластичность
$ упругость
$ жесткость
Способность элементов конструкций сопротивляться деформациям соответствует расчету на….
$$жесткость
$ прочность
$ пластичность
$ упругость
Для прямоугольной формы поперечного сечения осевые моменты инерции относительно осей, походящих через его центр тяжести
$$  $
$ 
$  $
$ 
Для круглой формы поперечного сечения осевые моменты инерции относительно осей, походящих через его центр тяжести
$$ 

$ 
$ 
$ 
$$$76. Как называется способность конструкции и ее элементов в определенных пределах воспринимать воздействие внешних сил без существенного изменения геометрической формы и размеров, т.е. свойства тела получать упругую деформацию:
$$ упругость
$ текучесть
$ пластичность
$ хрупкость
$$$77. Каким интегралом определяется геометрическая характеристика осевого момента инерции сечения  относительно оси
относительно оси  :
:
$$ 
$ 
$ 
$ 
$$$78. Какая формула используется для нахождения момента инерции круглого сечения:
$$ 
$ 
$ 
$ 
Для прямоугольного треугольника осевые моменты инерции для осей проходящих через центр тяжести
$$ 
$ 
$ 
$ 
$$$80. Как называется свойство материала, склонное к разрушению при весьма малых остаточных деформациях:
$$ хрупкость
$ пластичность
$ жесткость
$ упругость
$$$81. Как называется способность материала сохранять под нагрузкой первоначальную форму равновесия:
$$ пластичность
$ жесткость
$ устойчивость
$ хрупкость
Две взаимно перпендикулярные оси, относительно которых центробежных момент инерции равен нулю, называются
$$ главными осями инерции сечения
$основными осями сечения
$ вспомогательными осями сечения
$ дополнительными осями сечения
Для каких материалов наиболее опасна концентрация напряжений?
$$ хрупких
$ вязких
$ вязко упругих
$ для всех
Интенсивность внутренних сил, передающихся в точке через выделенную площадку, называется
$$ напряжением
$ равномерно распределенной нагрузкой
$ продольной силой
$ моментом
Плоское напряженное состояние. Чистый сдвиг. Угол сдвига равен, модуль сдвига материала. Чему равны касательные напряжения?
$$ 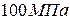
$ 
$ 
$ 
Какая-либо величина (напряжение, деформация, перемещение и т.д.), вызываемая несколькими силами, равна сумме величин, создаваемых каждой силой в отдельности. Данное утверждения называется
$$ принципом суперпозиции
$ принципом Сен-Венана
$ гипотезой плоских сечений
$ законом парности
Как называется напряженное состояние, если наряду с изгибающим моментом, в поперечном сечении стержня возникают и поперечные усилия?
$$ изгиб
$ растяжение
$ сдвиг
$ кручение






