$$ величиной, точкой приложения и линией действия
$ точкой приложения
$ линией действия
$ величиной
Системой сходящихся сил называется
$$ совокупность сил, линия действия которых пересекаются в одной точке
$ система уравновешенных сил
$ взаимно-перпендикулярная система сил
$ эквивалентная система сил
Реакция невесомого стержня направлена
$$ по оси симметрии стержня
$ по нормали
$ по касательной
$ перпендикулярно оси
Как направлена реакция гладкой плоскости?
$$ перпендикулярно плоскости
$ параллельно плоскости
$ под углом трения к плоскости
$ параллельно силе тяжести
Сходящиеся силы уравновешиваются, если их равнодействующая равна
$$ нулю
$ главному вектору
$ главному моменту
$ уравновешивающей силе
Основной характеристикой пары сил является
$$ момент пары сил
$ плечо пары сил
$ плоскость расположения
$ сила пары
Условия равновесия произвольной пространственной системы сил записываются в виде
$$ 
$ 
$ 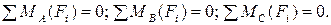
$ 
$$$39. Равнодействующей системы сил называется сила,
$$ эквивалентная некоторой системе сил, т.е. оказывающая на тело такое же действие, как и система сил
$ уравновешивающая сил, действующих на данное тело
$ равная геометрической сумме сил, действующих на данное тело
$ равная сумме модулей сил, действующих на данное тело
Моментом силы относительно точки называется
$$ произведение модуля силы на кратчайшее расстояние от линии действия силы до точки
$ алгебраическая величина, равная произведению проекций силы на плоскость, перпендикулярную этой оси, на расстояние от точки пересечения оси с плоскостью до линии действия проекции силы
$ произведение модуля силы на расстояние от конца вектора силы до точки
$ произведение модуля силы на косинус угла между линией действия силы и положительным направлением оси
Моментом силы относительно оси называется
$$ алгебраическая величина, равная произведению проекций силы на плоскость, перпендикулярную этой оси, на расстояние от точки пересечения оси с плоскостью до линии действия проекции силы
$ произведение модуля силы на косинус угла между линией действия силы и положительным направлением оси
$ произведение модуля силы на расстояние от конца вектора силы до точки
$ произведение модуля силы на кратчайшее расстояние от линии действия силы до точки
Моментом пары называется
$$ произведение модуля одной из сил на ее плечо
$ произведение модуля силы на расстояние между точками приложения сил
$ произведение модуля силы на расстояние между концами сил
$ произведение модуля силы на расстояние от линии действия одной силы до точки приложения другой силы
$$$43. Интенсивность есть сила,
$$ приходящаяся на единицу длины нагруженного участка
$ сосредоточенная
$ уравновешивающая
$ равнодействующая






