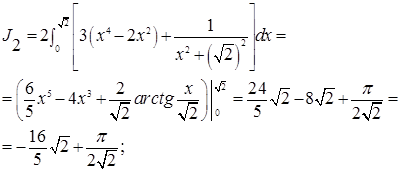Для определенных интегралов имеет место формула интегрирования по частям, аналогичная той, которая была получена для неопределенного интеграла
Пусть 
на 
имеем: 
По формуле Н-Л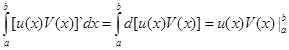 
и кроме того
Откуда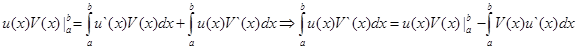 
или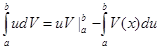 
ч.т.д.
а обобщенная формула интегрирования по частям перейдет в такую:
При этом по прежнему функции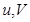 
и все встречающиеся производные предполагаются непрерывными.
ример 1.
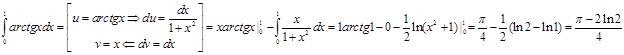
Пример 2 
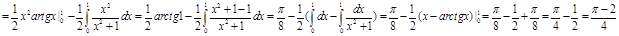
Замена переменного под знаком определенного интеграла
Пусть требуется вычислить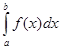 
от 
. Иногда, как в неопределенном интеграле бывает удобно произвести замену перестановкой «х» на новую переменную t, которые связаны между собой соотношением:
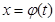
Докажем относительно такой замены теорему
Th2. Пусть выполнены следующие условия:
1. Уравнения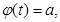 
и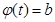 
имеют решения
(Обозначим их соотвественно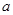 
и 
, так что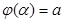 
, 
)
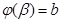2. Функция 
(имеет непрерывную производную 
на )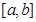
3. При изменении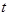 
на отрезке 
значение функции 
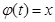не выходит из отрезка 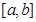(т.е 
) и следовательно сложная функция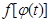 
определена (или 
).
Тогда имеет место равенство:
(1)
Называемое формулой замены переменной под знаком определенного интеграла
Доказательство
Пусть
на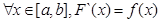 
, тогда по формуле Ньютона-Лейбница имеем 
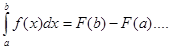(2), рассмотрим на 
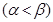функцию 
переменного t определенную соотношением 
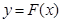и 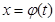. Вычислим ее производному по правилу сложной функции:
что функция является первообразной для функции 
на сегменте .
Тогда по формуле Ньютона-Лейбница (которая здесь применима, т.к. функция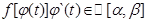 
) имеем:
(3)
(т.к. по условию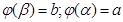 
)
Сопоставляя равенства (2) и (3) мы и получим доказываемую формулу (1)
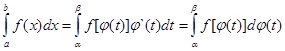(1) ч.т.д
амечание.
При использовании формулы (1) ф-ю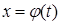 
следует стараться выбрать так, чтобы новый интеграл был более простым для вычисления, чем первоначальный.
Пределы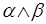 
нового интеграла определяются из уравнени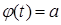й: 
и 
. При этом эти уравнения могут иметь по несколько корней, тогда за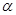 
можно принять любой корень уравнения 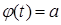, а за 
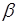любой корень уравнения
Лишь бы выполнялись условия 2 и 3 th. Условие th3 окажется, в частности, наверняка выполненным, если ф-я 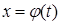будет монотонной на [a,b]
Поэтому на практике замену переменного осуществляют с помощью монотонных функций.
Если ф-я 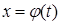не может принимать значений, равных пределам интегрирования a и b, то она не может служить для выполнения замены переменного в этом интеграле.
нтегрирование четных и нечетных функций.
Th Пусть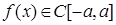 
на симметричном относительно начала координат сегменте.
Тогда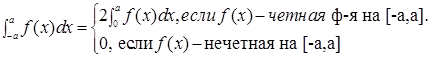 
Док-во
ример 1.
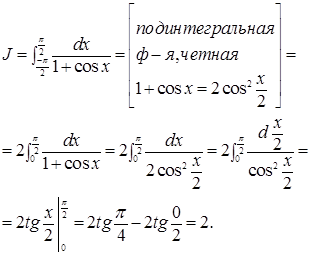
Пример 2.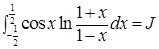 
Решение. Ф-я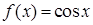 
четна. Докажем, что ф-я 
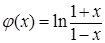нечетна;
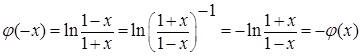
Т.О., подынтегральная ф-я представляет собой произведение четной и нечетной функции, т.е является 
– нечетная ф-я, поэтому J=0
Замечание. Если ф-я f(x) периодическая с периодом Т то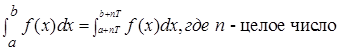 
Пример 3.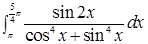 
Решение. Подынтегральная ф-я является периодической с периодом Т=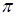 
, т.к
Поэтому от верхнего и нижнего пределов интегрирования можно отнять число π:
Пример 4. Вычислить интеграл.
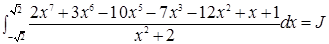
Решение.
Мы разложили ин-л J в сумму двух интегралов Т.О., чтобы под знаком первого ин-ла стояла нечетная ф-я, а под знаком второго интеграла – четная функция. Тогда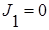 
.
