войства определенного интеграла.
I) Аддитивность (от лат-го additivus – прибавленный) интеграла, как функции отрезка интегрирования.

(пусть  , тогда
, тогда  )
)
(б/д)
Df 1 При a=b положим 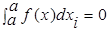 - интеграл с одинаковыми пределами интегрирования = 0
- интеграл с одинаковыми пределами интегрирования = 0
Df 2 При a>b положим  , если один из интегралов
, если один из интегралов  (т.е при перестановке между собой верхнего и нижнего пределов интегрирования интеграл умножается на -1)
(т.е при перестановке между собой верхнего и нижнего пределов интегрирования интеграл умножается на -1)
Эти определения естественно обобщают введенное ранее определение определенного интеграла. При этом в интегральных суммах нужно ввести понятие ориентированного отрезка и считать, что
 , если
, если 
 , если
, если 
(2) Пусть f(x) – интегрируема на большем из отрезков [a,b], [a,c], [c,b].
 |
а с b
a<c, a<b, c<b (a<c<b) => f(x) интегрируема на 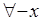 двух других отрезках и справедлива формула.
двух других отрезках и справедлива формула.  (б/д)
(б/д)
Df Положим 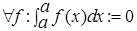
Для функции  , где a<b, положим
, где a<b, положим

Т.е при перестановке между собой верхнего и нижнего пределов интегрирования определенный интеграл умножается на «-1».
II Свойства, связанные с арифметическими действиями над подынтегральными функциями
инейность
Пусть  и справедлива формула:
и справедлива формула:
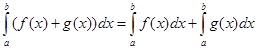
Док-во
Возьмем 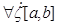 . Тогда
. Тогда  , тогда:
, тогда:

 предел из соответствующего равенства следует из свойств пределов
предел из соответствующего равенства следует из свойств пределов
Замечание. Свойство (3) может быть обобщено на конечную сумму интегрируемых функций
днородность

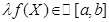
И справедливо равенство:

5) Пусть  и
и 
а) 
б)  если
если 
Док-во
Возьмем 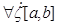
тогда  , тогда
, тогда 
амечание.
Свойство (5а) может быть обобщено на конечное произведение интегрируемых функций
III Некоторые оценки интеграла
Пусть 



Доказательство
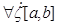 , составим интегральную сумму:
, составим интегральную сумму:
 используя свойства пределов (теорема о переходе к пределу в неравенствах) при
используя свойства пределов (теорема о переходе к пределу в неравенствах) при  , перейдем в (*) к пределу и получим:
, перейдем в (*) к пределу и получим:

Следствие из (6)
Пусть  и
и 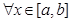

Доказательство следует из свойства (6), если обозначить  и использовать свойство линейности
и использовать свойство линейности 
(7) Пусть  и
и 
Доказательство
Т.к.  , то
, то  . Применяя следствие из теоремы 6 к неравенствам
. Применяя следствие из теоремы 6 к неравенствам
 получим неравенства:
получим неравенства:
 , которое можно записать как одно неравенство
, которое можно записать как одно неравенство 
Т.е. абсолютная величина интеграла от непрерывной функции не больше интеграла от абсолютной величины этой же функции
Следствие из (7)

По свойствам (6) и (7)

(8) Пусть  определена на
определена на  за исключением конечного числа точек
за исключением конечного числа точек 
(б/д).
В частности, отсюда вытекает, что если
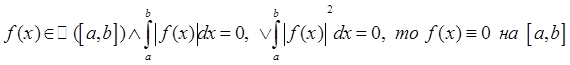
Следствие из (8)
Пусть  за исключением конечного числа точек
за исключением конечного числа точек
 одновременно или интегрируемы, или не интегрируемы на
одновременно или интегрируемы, или не интегрируемы на 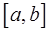 и, если интегрируемы, то
и, если интегрируемы, то 
Доказательство следует из свойства (8) и свойства линейности  , если положить
, если положить 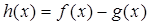
амечание.
Согласно свойству (8) можно рассматривать интегралы от ограниченных функций, не определенных в конечном числе точек  . Для этого необходимо доопределить произвольным образом функцию в
. Для этого необходимо доопределить произвольным образом функцию в 
IV Теорема о среднем.
(9) Пусть:

Тогда
 , что
, что
 … (1)
… (1)
ок-во.
Отметим, во-первых 
Действительно  - ограниченная на [a,b] =>
- ограниченная на [a,b] =>
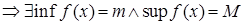

 , как произведение интегрируемых функций
, как произведение интегрируемых функций
Положим далее для определенности a<b
И 
 . Другие случаи доказываются аналогично.
. Другие случаи доказываются аналогично.
Очевидно: 

 , проинтегрируем это выражение по [a,b]:
, проинтегрируем это выражение по [a,b]:

Возможны два варианта (из сво-ва (6))

Но тогда (1) выполняется  .
.
 Разделим (2) на
Разделим (2) на 

ледствие. А.
Пусть  и сохранит знак
и сохранит знак  :
:

Док-во
Условия св-ва (9) выполнены => справедлива формула  (1)
(1)
Но т.к  , то по th о промежуточном значении непрерывных на отрезке функций
, то по th о промежуточном значении непрерывных на отрезке функций
 3)
3) 
ледствие. В.
Пусть 
Что  4)
4)
Док-во => из свойства (9), если положить 
ледствие С.
Пусть 
 5)
5)
Док-во следует из следствия А, если положить  . Равенство 5) чаще всего называют теоремой о среднем значении. Оно имеет простой геометрический смысл.
. Равенство 5) чаще всего называют теоремой о среднем значении. Оно имеет простой геометрический смысл.
Df:  - называют криволинейной трапецией.
- называют криволинейной трапецией.
 прямоугольник с высотой
прямоугольник с высотой 
где  равновеликая криволинейная трапеция с основанием [a,b]
равновеликая криволинейная трапеция с основанием [a,b]


амечание.
Помимо классов функций  введем классы
введем классы
 , где
, где  - множество всех функций f(x), определенных и ограниченных на [a,b];
- множество всех функций f(x), определенных и ограниченных на [a,b];
 - множество всех функций f(x), определенных и монотонных на [a,b].
- множество всех функций f(x), определенных и монотонных на [a,b].
Тогда:
 .
.
пределенный интеграл с переменным верхним пределом. Формула Ньютона-Лейбница.
Мы рассматривали интегралы с постоянными пределами интегрирования  , где a и b – const
, где a и b – const
Величина такого интеграла для данной подынтегральной функции зависит только от пределов интегрирования “a” и “b” и не зависит от x.
Если менять, например, верхний предел “b”, то величина интеграла станет некоторой функцией от переменной “x”.
Df1 Пусть 

С переменным верхним пределом интегрирования.
Обозначим переменную интеграла в  буквой t, чтобы не смешивать ее с верхним пределом x, т.е
буквой t, чтобы не смешивать ее с верхним пределом x, т.е  .
.
Аналогично 
 - интеграл с переменным нижним пределом.
- интеграл с переменным нижним пределом.
Рассмотрение ин-ла  как функции нижнего предела не представляет специального интеграла, т.к в силу свойств интеграла
как функции нижнего предела не представляет специального интеграла, т.к в силу свойств интеграла 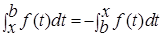 Задача свелась к изучению интеграла как функции верхнего предела.
Задача свелась к изучению интеграла как функции верхнего предела.
Относительно этой функции докажем следующие теоремы.
Th1 (о непрерывности определенного интеграла Римана как функции верхнего предела)

Док-во
Пусть  имеем, в силу аддитивности интеграла Римана
имеем, в силу аддитивности интеграла Римана 


 - ограничена на [a,b], т.е
- ограничена на [a,b], т.е 
Отсюда:




Но т.к  ч.т.д
ч.т.д
Th2 (Диф-ность  ) (2й вариант док-ва)
) (2й вариант док-ва)
(О диф-ти О.И.Римана, как функции верхнего предела)


Док-во
Из th1 известно, что  и
и  (1),
(1), 
Применим к ин-лу (1) th-му о среднем, т.е 
Найдем производную функции 
 …(*)
…(*)
Т.к  , то
, то  или
или 
th доказана.

 - есть первообразная, для f(x) на [a,b].
- есть первообразная, для f(x) на [a,b].
Т.О. если  , то
, то  (инт.
(инт.  )
)
По его переменному верхнему пределу x на этом сегменте  и равна значению f(x) подынтегральной функции f(t) при t=x
и равна значению f(x) подынтегральной функции f(t) при t=x
Тогда => th-мы.
Th a) Если  , то ф-я
, то ф-я  ,
,  .
.
Является первообразной для ф-и f(x) на этом сегменте ([a,b]).
Th б)  - ф-я имеет на ней первообразную.
- ф-я имеет на ней первообразную.
бъяснение.

В равенстве (*) использована непрерывность:
Если 
 , а значит
, а значит
 . Т.к f-непр. Ф-я, то отсюда =>,
. Т.к f-непр. Ф-я, то отсюда =>,
Что  . Или
. Или 
 th доказана.
th доказана.
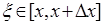
Когда  тогда
тогда  , то
, то  .
.
амечание.
Если x=”a” или “b”, то под  следует подразумевать односторонние производные.
следует подразумевать односторонние производные.
Следствие 1) 
1.  есть первообразная для f(x) на [a,b]
есть первообразная для f(x) на [a,b]
2.  первообразная для f(x) на [a,b]
первообразная для f(x) на [a,b]
Док-во (1) следует из th2 т.к f(x) – непрерывна  .
.
Пункт (2) Первообразная действительно  .
.
В равенстве (*) использована непрерывность: если  , то
, то  , а значит и
, а значит и  .
.
Так как f непрерывная функция, то отсюда следует, что  .
.
Итак,  , th-ма доказана.
, th-ма доказана.
Например  .
.
Отметим, что теорема 2 доказывает фактически 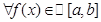 следующую формулу.
следующую формулу.

Т.к операция интегрирования есть обратная к диф-нию.
Кроме того доказана связь неопределенного интеграла и определенного

ледствие 2
 для
для 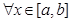
Доказательство

Т.к. 
Т.к. 
Th 3 Основная теорема интегрального исчисления
Пусть  и
и  - первообразная на
- первообразная на 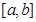 для
для  , тогда
, тогда

Формула Ньютона-Лейбница
Для обозначения разных  удобно использовать так называемый знак подстановки
удобно использовать так называемый знак подстановки 
Доказательство
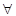 -е две переменные функции f(x) заданой на [a,b], отличаются на постоянную
-е две переменные функции f(x) заданой на [a,b], отличаются на постоянную
Если  , а
, а  другая первообразная непрерывной функции f(x), то
другая первообразная непрерывной функции f(x), то  , т.е.
, т.е.  положим в формуле х=а, а затем х=b. Как нам известно
положим в формуле х=а, а затем х=b. Как нам известно  для
для 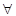 -й функции, принимающей конечное значение в (.) а. Поэтому
-й функции, принимающей конечное значение в (.) а. Поэтому 
Th Для того чтобы вычислить  по
по 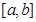 от
от  , следует вычислить значение произвольной ее первообразной в (.) «
, следует вычислить значение произвольной ее первообразной в (.) « » и в (.) «
» и в (.) « » и вычесть из первого значения второе
» и вычесть из первого значения второе
Теперь мы имеем правила вычисления  от широкого класса интегрируемых функций.
от широкого класса интегрируемых функций.
Доказательство
По следствию (1) теоремы 2  - первообразная
- первообразная  на
на 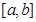 . Т.о.
. Т.о.  - две первообразные
- две первообразные 

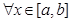
Пусть х=а 
Т.е.  (*)
(*)
Пусть  в(*)
в(*) 
Пример
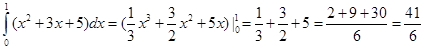
Формула 
Формула Ньютона-Лейбница
С помощью символа подстановки  формулу (1) запишем в виде
формулу (1) запишем в виде 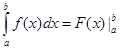 …(2)
…(2)
Формула (2) устанавливает зависимость между определённым и неопределенными интегралами функций 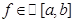 , множество (…) разрыва которой не более чем счетно, выражаемую формулой
, множество (…) разрыва которой не более чем счетно, выражаемую формулой  (3)
(3)
§5 Замена переменной в определенном интеграле. Интегрирование по частям
еорема 1
Пусть
1. 
2. 
3. 
4. 

Тогда  (1)
(1)
Доказательство

Т.к.  -первообразная на
-первообразная на  и
и 

По теореме о замене переменной в неопределенном интеграле  -первообразная для
-первообразная для  на
на  (и на
(и на  )
)

Отсюда  (1)
(1)
Отметим, что при  в доказательстве должны фигурировать соответствующие односторонние производные.
в доказательстве должны фигурировать соответствующие односторонние производные.
В случае, если 


При некоторых t,  может выходить за отрезок
может выходить за отрезок  . Но обязательно
. Но обязательно 
Пример 

Этот интеграл можно вычислить и без теоремы 1

Нам известен неопределенный интеграл
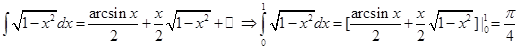
(По формуле 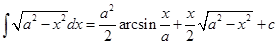 )
)






