рименимость метода симметричных составляющих к исследованию переходных процессов

Из курса теоретических основ электротехники известно, что в электрических устройствах, выполненных симметрично, применение метода симметричных составляющих в значительной мере упрощает анализ несимметричных процессов, так как при этом симметричные составляющие токов связаны законом Ома с симметричными составляющими напряжений только одноименной последовательности. Иными словами, если какой-либо элемент цепи симметричен и обладает по отношению к симметричным составляющим токов прямой, обратной и нулевой последовательностей соответственно сопротивлениями Z₁, Z₂, Z_o, то симметричные составляющие падения напряжения в этом элементе будут:

₁ = Z_{1 1} (11-1)

₂ = Z_{2 2} (11-2)

₀ = Z_{0 0} (11-3)

Сопротивления Z₁, Z₂ и Z_o для сокращения обычно называют сопротивлениями соответственно прямой, обратной и нулевой последовательностей. Их величины для одного и того же элемента в общем случае различны.

Из изложенного, казалось бы, уже можно сделать вывод, что если временные величины в рассматриваемом процессе могут быть разложены на системы симметричных составляющих и тогда известный метод симметричных составляющих в своей обычной форме может быть применен к исследованию несимметричных переходных процессов. Однако такой вывод был бы еще преждевременным.

Дело в том, что, как показано выше, у синхронной машины с несимметричным ротором возникающее при несимметричном режиме инверсное магнитное поле статора порождает прямое магнитное поле статора, вращающееся с соответственно большей скоростью. Обращаясь к терминологии метода симметричных составляющих, можно сказать, что это равносильно тому, что магнитное поле обратной последовательности, созданное системой токов обратной последовательности какой-либо частоты, вызывает магнитное поле прямой последовательности и связанную с ними систему токов прямой последовательности, порядковые номера частот которых на два больше соответствующего номера частоты токов обратной последовательности. Другими словами, при этом оказываются взаимно связанными системы токов прямой и обратной последовательностей разных частот, что налагает дополнительные условия и требования на метод симметричных составляющих. Что касается системы токов нулевой последовательности, то создаваемое ими результирующее магнитное поле в расточке статора при любой частоте практически близко к нулю и никакой магнитной связи с ротором не создает.

Дальнейшее развитие представлений метода симметричных составляющих применительно к синхронным машинам с несимметричным ротором в условиях установившихся режимов и переходных процессов при нарушении симметрии впервые дано Н. Н. Щедриным. Помимо математического обоснования такого развития,импредложены для учета высших гармоник специальные цепные схемы, применение которых особенно эффективно при выполнении расчетов с помощью моделей или иных расчетных установок.

В подавляющем числе практических расчетов несимметричных переходных процессов обычно ограничиваются учетом лишь основной гармоники токов и напряжений. Именно только при таком допущении представляется возможным применять метод симметричных составляющих в его обычной форме, характеризуя для этого синхронную машину в схеме обратной последовательности соответствующей реактивностью х₂.

Остановимся еще на одном вопросе, в понимании которого часто встречаются трудности.

Протекающие по обмоткам статора токи прямой, обратной и нулевой последовательностей создают магнитные потоки тех же последовательностей. Последние наводят в статоре соответствующие ЭДС. Вводить эти ЭДС в расчет нецелесообразно, так как они пропорциональны (при пренебрежении насыщением магнитной системы машины) токам отдельных последовательностей, значения которых еще подлежат определению. Поэтому в дальнейшем вводим в расчет только те ЭДС, которые или известны, или не зависят от внешних условий цепи статора, причем в силу симметричного выполнения статорной обмотки эти ЭДС являются ЭДС только прямой последовательности. Что касается ЭДС, обусловленных реакцией токов отдельных последовательностей, то их учитываем в виде падений напряжений с обратным знаком в соответствующих реактивностях машины.

Из изложенного следует, что при принятом способе учета ЭДС, обусловленных реакцией токов отдельных последовательностей, образование токов обратной и нулевой последовательностей можно представить как следствие возникающих в месте короткого замыкания напряжений обратной и нулевой последовательностей.

Таким образом задача расчета несимметричных КЗ связана с нахождением шести неизвестных: трех симметричных составляющих токов и трех составляющих напряжений.

Для их нахождения при любом виде КЗ всегда будем использовать три уравнения, соответствующие второму закону Кирхгофа.

;

;

,

где _к1, _к2, _к0, _к1 ,, _к2, _к0 —симметричные составляющие напряжения и тока в месте короткого замыкания;

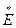_1S - результирующая ЭДС относительно точки короткого замыкания;

x_1S, x_2S, x_0S — результирующие сопротивления схем соответствующих последовательностей относительно точки короткого замыкания.

Недостающие три уравнения легко получить из граничных условий, которыми характеризуется тот или иной вид несимметричного повреждения.

Все соотношения будем записывать для особой фазы, т.е. фазы, которая находится в условиях, отличающихся от условий, в которых находятся другие фазы. В качестве особой фазы всегда будем принимать фазу А.

 

Параметры элементов для токов обратной и нулевой последовательностей

бщие замечания

Все сопротивления, которыми характеризуются отдельные элементы в нормальном симметричном режиме, а также в симметричном переходном процессе, по существу являются сопротивлениями прямой последовательности. Этот термин вводить ранее не было нужды, поскольку токи были лишь одной последовательности.

При отсутствии магнитной связи между фазами какого-либо элемента его сопротивление не зависит от порядка чередования, фаз тока. Активная и реактивная слагающие сопротивления такого элемента зависят только от частоты тока и, следовательно, для всех последовательностей одинаковы, т. е.

; ; .

Такими элементами можно практически считать реакторы.

Для элемента, магнитносвязанные цепи которого неподвижны относительно друг друга, сопротивления прямой и обратной последовательностей одинаковы, так как от перемены порядка чередования фаз симметричной трехфазной системы токов взаимоиндукция между фазами такого элемента не изменяется.

Таким образом, для трансформаторов, автотрансформаторов, воздушных линий, кабелей и реакторов имеем:

; ;

Система токов нулевой последовательности резко отличается от систем токов прямой и обратной последовательностей, вследствие чего сопротивления нулевой последовательности в общем случае весьма существенно отличаются от соответствующих сопротивлений двух других последовательностей.

Для элементов, магнитносвязанные цепи которых подвижны относительно друг друга, сопротивления всех последовательностей будут различными (электрические машины).

Таким образом, для электрических машин имеем:

; ; .

 

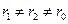Для турбогенераторов и явнополюсных машин с демпферными обмотками

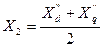
Для явнополюсных машин без ДО .

При отсутствии некоторых данных рекомендуется принимать для СМ с ДО 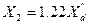, а для СМ без ДО .

В приближенных расчетах принимают для СМ с ДО .

Для АД принимают или .

Нагрузки в схемах обратной последовательности обычно представляют неизменными поперечно включенными сопротивлениями для некоторого типичного состава электроприемников. При основной частоте можно приближенно принимать в относительных единицах:

- для нагрузок, присоединенных к сети 6-10 кВ Z_2*=0.18+j0.24;

- для нагрузок, присоединенных к сети 110 кВ Z_2*=0.19+j0.36.

Эти значения сопротивлений отнесены к полной рабочей мощности нагрузки и к номинальному напряжению сети, к которой она присоединена.

Сопротивления токам нулевой последовательности

В синхронных машинах с симметричными обмотками магнитные потоки в обмотках статора, создаваемые токами нулевой последовательности, должны полностью компенсироваться. Практически, обмотки статора имеют некоторую несимметрию. Поэтому .

Для реакторов расстояние между катушками достаточно велико, что обуславливает малую взаимоиндукцию между катушками. Поэтому приближенно принимают .

оздушные линии.

В воздушных линиях токи нулевой последовательности, проходящие по фазным проводам линии, возвращаются в заземленные нейтрали через землю. Поскольку система токов нулевой последовательности не уравновешена (сумма токов фаз не равна нулю), создаваемый ею магнитный поток наводит в контурах, расположенных вблизи линии, ЭДС, которые вызывают в них компенсирующие токи. При таких условиях сопротивление линии токам нулевой последовательности существенно отличается от сопротивления линии токам прямой последовательности. Главная трудность достоверного определения сопротивления линии токам нулевой последовательности связана с учетом распределения тока в земле.

Продольное сопротивление нулевой последовательности Zo линии зависит от сопротивления Z_L петли «провод-земля» и сопротивлений взаимной индукции Z_М между двумя линиями «провод-земля». Рассмотрим влияние соседних фаз трехфазной одноцепной линии с тросом на сопротивления линии различных последовательностей при пренебрежении активным сопротивлением и емкостной проводимостью линии (рис. 1).

Если напряжение, приложенное к одному из концов транспонированной ЛЭП, замкнутой накоротко на другом конце, теряется в ее полном сопротивлении. Выражение для определения напряжения прямой последовательности фазы А имеет вид:

где X_L, X_M – реактивные сопротивления самоиндукции фазы и взаимоиндукции соответственно.

Можно получить такое же выражение и без операторов поворота. Известно, что . Тогда в заменим сумму токов и получим

При транспонированной трехфазной линии взаимная индуктивность всех фаз одинакова, в результате чего

Х1= X_L- X_M =Х2 или X_L=Х1+ X_M

Если к той же линии приложить напряжение нулевой последовательности, то

Таким образом

С учетом выражения X_L=Х1+ X_M имеем

 

Индуктивные сопротивления X_L, X_M зависят от удельной проводимости земли и частоты тока. Кроме того X_L зависит от радиуса провода, а X_M – от расстояния между проводами ВЛ.

Индуктивность линии «провод-земля» может быть получена как индуктивность эквивалентной двухпроводной линии с расстоянием между проводами D_З (рис. 2), называемого эквивалентной глубиной возврата тока через землю, зависит от проводимости земли l и частоты тока f. По Карсону

 

В зависимости от почвы значение D_З находится в пределах от 94 м до 30000 м. При отсутствии данных о проводимости земли в качестве среднего значения D_З обычно принимают 1000 м, что значительно больше высоты подвеса провода h. Таким образом, реактивность линии «провод-земля» легко определить по формуле для двухпроводной линии

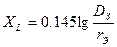, Ом/км, r_Э – эквивалентный радиус провода, значения которого составляют:

r_Э=0,779r –для сплошных круглых проводников из немагнитного материала;

r_Э=(0,724-0,771)r – для витых медных проводников;

r_Э=0,95 r – для алюминиевых и сталеалюминиевых проводов;

r – истинный радиус провода.

Для линий с расщепленными проводами вместо r_Э следует водить средний геометрический радиус r_СР, определяемый по , где n – число проводов в фазе, - среднее геометрическое расстояние между проводами одной фазы.

Активное сопротивление линии «провод-земля» складывается из активного сопротивления провода r_П и дополнительного сопротивления r_З, учитывающего потерю активной мощности в земле от протекающего в ней тока, т.е.

r = r_П + r_З, где r_З =fp²10^-4 Ом/км, которое при 50 Гц равно 0,05 Ом/км.

Сопротивление, обусловленное взаимоиндукцией между двумя параллельными линиями «провод-земля» с расстоянием d между осями их проводов можно определить из выражения

Ом/км, где активная составляющая соответствует потере активной мощности, возникающей от протекания тока в земле. Для трехфазной одноцепной линии с полным циклом транспозиции проводов сопротивление взаимоиндукции между фазами при возврате тока через землю, очевидно, следует определять из среднегеометрического расстояния между проводами фаз а, в, с , т.е.

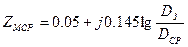
Учтем в найденные значения составляющих

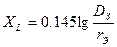и после преобразований с учетом - средний геометрический радиус системы трех проводов получим

Таким образом, в системе прямой и обратной последовательностей взаимоиндукция фазы, принятой за основную, с соседними фазами уменьшает индуктивное сопротивление линии, а в системе нулевой последовательности взаимоиндукция приводит к увеличению магнитного потока фазы.

При наличии на линии хорошо проводящего заземленного троса, сопротивление нулевой последовательности линии уменьшается за счет взаимоиндукции петли трос-провод, так как тока в тросе направлены навстречу токам в проводе (рис. 1). Плохопроводящий, стальной трос незначительно уменьшает Х0 линии.

При наличии параллельных цепей и КЗ за пределами линии или на концах цепей сопротивление нулевой последовательности каждой линии увеличивается за счет взаимоиндукции с соседней цепью. Реактивность взаимной индукции нулевой последовательности между двумя параллельными цепями I и II Х_I-II0, где

, а - среднегеометрическое расстояние между цепями I и II (d_aa и т.д. – расстояния от каждого провода одной цепи до каждого провода другой цепи). В литературе приведены соотношения для расчета дополнительного сопротивления для различных вариантов конфигурации линии, которые вычисляют на основе теории многополюсников.

При выполнении упрощенных расчетов сопротивления нулевой последовательности линий можно принимать по табл. 3.

 

Характеристика ВЛ	Отношение х0 / х1
Одноцепная без тросов	3,5
Одноцепная со стальным тросом	3,0
Одноцепная с заземленным хорошо проводящим тросом	2,0
Двухцепная без тросов	5,5
Двухцепная со стальным тросом	4,7
Двухцепная с заземленными хорошо проводящим тросом	3,0

 

Сопротивление кабелей. Активное и индуктивное сопротивления прямой последовательности кабеля равны соответствующим сопротивлениям обратной последовательности. В ориентировочных расчетах для трехжильных кабелей можно принимать

рансформаторы.

Сопротивление нулевой последовательности трансформаторов со стороны обмотки, соединенной в треугольник или в звезду с незаземленной нулевой точкой, равно бесконечности (необходимо рассматривать КЗ с землей, возникшее со стороны указанных обмоток).

Условия для протекания токов нулевой последовательности могут возникнуть при приложении напряжения нулевой последовательности к обмотке, соединенной в звезду с заземленной нейтралью (при КЗ с землей на выводах указанной обмотки). Условия определяются схемой соединения других обмоток и наличия в их цепях контуров для прохождения токов нулевой последовательности. Схемы замещения трансформаторов для токов нулевой последовательности при различных вариантах соединения обмоток приведены ниже. Справа против каждого варианта соединения обмоток изображены схемы замещения трансформатора для токов нулевой последовательности (X_I, X_II, X_III реактивные сопротивления рассеяния обмоток I, II, III; X_m0 – реактивное сопротивление намагничивания нулевой последовательности трансформаторами; активными сопротивлениями пренебрегаем. Общим для всех вариантов является то, что напряжение нулевой последовательности обуславливает протекание токов нулевой последовательности в трех фазах обмотки I во всех вариантах и наводят ЭДС в других обмотках.

При соединении обмоток по схеме заземленная звезда треугольник наведенная ЭДС нулевой последовательности целиком расходуется на прохождение тока той же последовательности через реактивное сопротивление рассеяния обмотки, соединенной треугольником. Так как тока нулевой последовательности в фазах равны и не имеют сдвига по фазе, то выйти из треугольника, т.е. за пределы этой обмотки трансформатора они не могут. Вся ЭДС расходуется на падение напряжения от токов нулевой последовательности в обмотке, собранной треугольником. В схеме замещения это отражают закорачиванием ветви с X_II. Сопротивление нулевой последовательности трансформатора равно:

Так как сопротивление X_m0 значительно больше X_II, то , т.е. равно сопротивлению трансформатора токам прямой последовательности.

 

 

В варианте б показано, что в цепи обмотки II, которая соединена в звезду с заземленной нейтралью, имеется путь для протекания тока нулевой последовательности, так как в цепи обмотки II имеется еще одна заземленная нейтраль (см. штриховую линию). Таким образом наведенная ЭДС вызывает протекание тока в индуктивном сопротивлении рассеяния обмотки II и во всех элементах, которые имеются далее включая элемент с заземленной нейтралью, показанной штрихом

 

Сопротивление части схемы токам нулевой последовательности равно:

Так как сопротивление намагничивание значительно больше, то в методике расчета токов КЗ внесено допущение о не учете тока намагничивания. Таким образом, и в этом случае сопротивление трансформатора токам нулевой последовательности равно сопротивлению трансформатора токам прямой последовательности.

Ниже приведен вариант, в котором нейтраль обмотки разземлена. В этом случае пути для протекания тока нулевой последовательности нет, но ЭДС наведена, что соответствует режиму ХХ, при котором 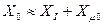. Значение X_m0 зависит от конструкции трансформатора. В группах из трех однофазных трансформаторов, а также в трехфазных трансформаторах с четырьмя и пятью стержнями имеется путь для замыкания магнитных потоков, что обуславливает малое магнитное сопротивление и значительное индуктивное X_m0 = ¥

Если магнитопровод трехобмоточного трансформатора трехстержневой, то магнитный поток замыкается по баку, воздуху, X_m0 = 0,3¸1 о.е., что больше индуктивного сопротивления рассеяния X_II и поэтому принимают X_m0 = ¥.

 

 

Следующие варианты связаны с трехобмоточными трансформаторами и автотрансформатором. Как известно, схема замещения токам прямо последовательности включает сопротивления трех обмоток. Анализ трехобмоточных трансформаторов можно выполнить опираясь на рассмотренные выше варианты двухобмоточных трансформаторов.

Так в варианте «г» обмотка II соединена в треугольник, поэтому индуктивное сопротивление этой обмотки вводится в схему замещения, а так как токи нулевой последовательности выйти за пределы этой обмотки не могут, что условно показано замыканием ветви в схеме замещения на землю.

Обмотка III соединена в звезду с разземленной нейтралью и поэтому не обеспечивается протекание тока нулевой последовательности и сопротивление равно ¥.

 

Следовательно, в этом случае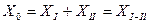

 

 

 

В варианте «д» обеспечивается путь для протекания тока от наведенной в обмотке III ЭДС через заземленную нейтраль элемента, связанного с обмоткой III штриховой линией на рисунке.

Обмотка II соединена треугольником, о котором уже сказано достаточно: ток протекает в обмотке, но выйти из него не может.

В этом случае

 

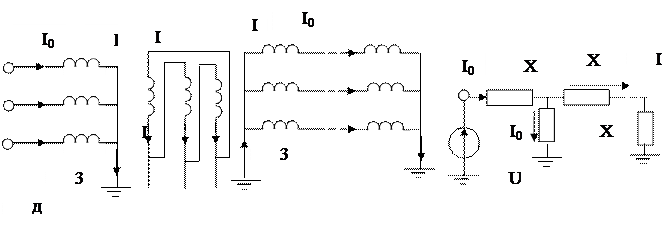В варианте «е» обмотки II и III соединены треугольником, поэтому

 

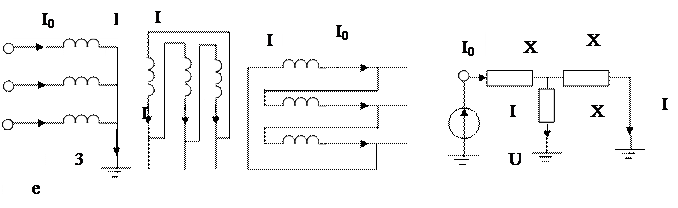Схема замещения автотрансформатора для токов нулевой последовательности имеет тот же вид, что и для трехобмоточного трансформатора при соответствующем соединении его обмоток. Напоминаем, что обмотки ВН, СН всегда соединены в звезду и по условиям безопасности нейтраль заземлена. Обмотка НН соединена в треугольник.

Ток в нейтрали автотрансформатора равен - токи нулевой последовательности первичной и вторичной обмотки, отнесенные к напряжению своей ступени.

 

 

Если в нейтрали трансформатора включено сопротивление, то оно вводится в схему замещения токам нулевой последовательности утроенной величиной последовательно за сопротивлением обмотки. Сопротивление утраивается так как через нейтраль замыкаются токи трех фаз, а схема составляется для одной фазы.

 

4. Схемы замещения отдельных последовательностей

Схемы замещения отдельных последовательностей включают в себя все элементы сети, по которым при данном виде несимметрии протекают токи соответствующих последовательностей.

Схема прямой последовательности эта та схема, которая составлялась при анализе любого трехфазного симметричного режима.

Схема замещения токам обратной последовательности по конфигурации аналогична схеме прямой последовательности. Различие состоит в том, что в схеме обратной последовательности значения ЭДС генераторов принимаются равными нулю, а также машина переменного тока вводят сопротивлением Х2.

Схемы замещения всех последовательностей имеют две характерные точки.

При поперечной несимметрии (несимметричные КЗ) концом схемы является точка, в которой возникло КЗ, а началом схемы точки нулевого потенциала. К концам схем приложены напряжения соответствующих последовательностей.

При продольной несимметрии (обрывы фаз) имеются две точки в месте обрыва. В месте обрыва приложены напряжения соответствующих последовательностей.

Схема замещения токам нулевой последовательности при поперечной несимметрии определяется трансформаторами, которые имеются в схеме. Составлять схему замещения токам нулевой последовательности следует начинать с места КЗ.

При продольной несимметрии напряжение нулевой последовательности вводится последовательно в фазные провода, циркуляция токов нулевой последовательности возможна даже отсутствии заземленных нейтралей, если при этом существует замкнутый контур той же электрически связанной цепи. Если таких путей нет, то все определяет наличие заземленных нейтралей.