1. Соответствие может быть задано перечислением всех упорядоченных пар, находящихся в соответствии G и соответствующих множеств (см. предыдущий пункт). Очевидно, что такой способ задания приемлем только для относительно небольших по мощности множеств.
2. Матричный способ. Соответствие G задаётся прямоугольной (квадратной) матрицей С = [ s ij ], где
3. Табличный способ. Для задания этим способом соответствия G проводят вертикали, каждой присваивают значение элемента первого множества А, затем горизонтали, которые получают имена второго элементов второго множества В. Затем жирными точками обозначают пересечение этих прямых, удовлетворяющих соответствию G. Иногда такая таблица называется графиком соответствия.
4. Графический способ. Элементы обоих множеств изображаются точками, кружочками или другими геометрическими фигурами. Стрелками же соединяются те элементы множеств, которые принадлежат данному соответствию. Стрелки направлены из области отправления (множество А) к области прибытия (множество В). Такой способ иногда называют стрелочным представлением соответствия.
5. С помощью сечений. Пусть (a, b) Î G. Тогда сечением множества G по элементу а (или левым сечением) называется множество, равное множеству образов этого элемента δ (a,G) = { b ç b ÎB, (а, b)ÎG}. Сечением G по элементу b (или правым сечением) называется множество, равное множеству прообразов этого элемента δ ─1 (b, G) = { a ç a ÎA, (а, b)ÎG}. Если под каждым элементом множества А записать соответствующее сечение, то получим новый способ задания соответствия G – с помощью сечений. Множество сечений соответствия G называется фактор-множеством по данному соответствия и обозначается F/G.
Задача 1. Задать бинарное соответствие на множествах всеми возможными способами.
А = {июнь, май, февраль, август, октябрь, январь, апрель, декабрь}; B = {зима, весна, лето, осень}; G = {(a, b) ç a ÎA, b ÎB; a - месяц времени года b }.
Решение. Для удобства элементы множества А обозначим числами: A = {6, 5, 2, 8, 10, 1, 4, 12}, a элементы множества В буквами: B = { z, w, l, o }. Это позволит нам в дальнейшем отвлечься от конкретного смысла элементов множеств и получить соответствие в формализованном виде.
Задание перечислением: G = {(6, l), (5, w), (2, z), (8, l), (10, o), (1, z), (4, w), (12, z)}. Это позволит нам в дальнейшем отвлечься от конкретного смысла элементов множеств и получить соответствие в формализованном виде.
Задание матричным способом:
Соответствие G состоит из восьми упорядоченных пар. Поэтому матрица С имеет 8 единиц, соответствующих этим парам. Остальные элементы матрицы нули, поскольку соответствующих пар в G нет.
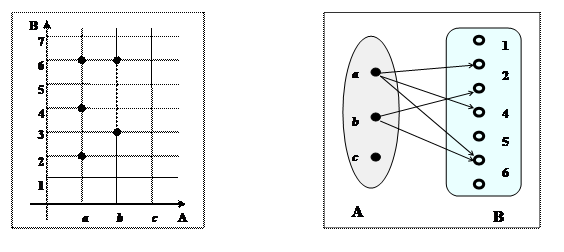
Задание табличным способом:
Полученная таблица напоминает привычный график, например, функции y = f (x), построение которого изучалось в курсе высшей математики. Здесь на оси абсцисс откладываются элементы первого множества (первая проекция соответствия), а на оси ординат – второго множества (вторая проекция).
Задание графическим способом.
Задание с помощью сечений. Сечения лучше всего определять по графику соответствия. Запишем матрицу, где первая строка – это элементы множества А, а вторая строка - соответствующие сечения по каждому элементу множества А:
Фактор-множество по соответствию G записано во второй строке: F/G = {{ z },{ w },{ l },{o}}.
Задача 2. Бинарное соответствие на множествах А = { a, b, c }; B = {1,2,3,4,5,6,7} задано перечислением: G = {(a,2), (b,3), (a,4), (a,6), (b,6)}. Рассмотреть иные способы задания этого соответствия.
Задание матричным способом:
Задание табличным способом: Задание графическим способом:
Задание с помощью сечений. 
.
Фактор-множество F/G = {{2,4,6},{3,6},{Æ}}.
Задачи для самостоятельного решения.
1. Задать бинарное соответствие на множествах всеми возможными способами.
А = {Т.Шевченко, А.Пушкин, Л.Украинка, Л.Толстой, У.Шекспир};
B = {«Анна Каренина», «Евгений Онегин», «Му-Му», «Сон», «Война и мир», «Гайдамаки», «Руслан и Людмила», «Заповіт», «Лісова пісня», «Каштанка»}.
G = {(a, b)ç a ÎA, b ÎB, a − автор b }.
2. На множествах A = {0,1,2,3,4} и B = {5,6,7,8,9} заданы соответствия:
a) G1 = {(1,5), (1,6), (2,6), (3,9), (4,9)};
b) G2 = {(0,6), (1,6), (2,7), (3,7),)4,9)};
c) G3 = {(0,6), (1,7), (2,5), (3,9), (4,8)}.
Задать соответствия всеми возможными способами.
ипы бинарных соответствий
Пусть задано некоторое соответствие G Í А´В = {(a, b)ç a ÎA, b ÎB, (a, b)ÎG}.
Соответствие называется всюду определённым ( или полностью определённым), если его область определения совпадает со всем множеством А: Dom(G) = А. Иными словами каждый элемент множества А участвует в парах (а, b)Î G и при этом каждому а Î А найдётся хотя бы один образ из множества В. Сечение по всякому элементу а Î А не будет пустым.
В противном случае соответствие называют частично определённым (или просто частичным).
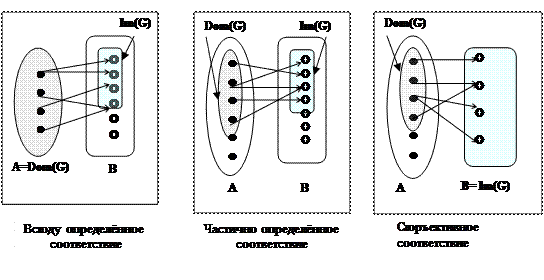
Соответствие G называется сюръективным, если его множество значений совпадает со всем множеством B: Im(G) = B. Иными словами каждый элемент b Î B участвует в парах (а, b)Î G, как минимум, один раз. То есть для каждого элемента b Î B найдется хотя бы один прообраз из множества А. Говорят, что при сюръективном соответствии покрывается всё множество В.
Соответствие G называется функциональным (или однозначным), если каждому элементу множества А соответствует не более одного элемента из множества В. Пары (a, b) такого соответствия не содержат одинаковых первых координат и различных вторых. Каждый элемент а Î А имеет не более одного образа b Î B. Среди функциональных также различают полностью определённые и частично определенные соответствия, равно как и сюръективные и не сюръективные.
 |  |
Функциональное соответствие Не функциональное соответствие
Соответствие G называется инъективным, если любой элемент b Î В имеет не более одного прообраза. Пары такого соответствия (a, b) не содержат одинаковых вторых и разных первых координат. При этом каждый элемент а Î А имеет не более одного образа.
Соответствие G называется биективным (или взаимно однозначным), если оно всюду определено, сюръективно, функционально и инъективно. В этом случае каждому элементу а Î А ставится в соответствие один и только один элемент b Î В. В парах (a, b) нет двух одинаковых первых элементов, вторых также.
Соответствие G называется отображением множества А в множество В (или просто А в В), если оно является всюду определенным и функциональным.
Соответствие G называется отображением множества А на множество В (или просто А на В), если оно является всюду определенным, функциональным и сюръективным.
Задача 1. На множествахА = { a, b, c, d, e } и В = {1,2,3} заданосоответствие G={(a,2), (b,3), (c,1), (d,2), (e,1)}. К какому из основных типов (всюду определённое, сюръективное, функциональное, инъективное) оно относится. Для удобства представить G графически (стрелочное изображение).
Решение.
- Соответствие является всюду определённым, так как пр1G = A;
- Соответствие является сюръективным, поскольку пр2G = В;
- Соответствие является функциональным, поскольку первые координаты пар не повторяются;
- Соответствие является не инъективным, так как элементы 1ÎВ и 2ÎВ имеют больше одного прообраза.
- Данное соответствие есть отображение А в В.
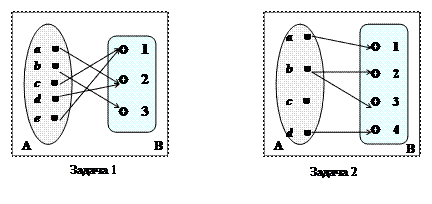
Задача 2. На множествахА = { a, b, c, d } и В = {1,2,3,4} заданосоответствие G={(a,1), (b,2), (b,3), (d,4)}. К какому из основных типов (всюду определённое, сюръективное, функциональное, инъективное) оно относится. Для удобства представить G графически (стрелочное изображение).
Решение.
- Соответствие является частично определённым, так как пр1G ≠ A (элемент с ÎА не встречается ни в одной паре);
- Соответствие является сюръективным, поскольку пр2G = В;
- Соответствие не является функциональным, поскольку первые координаты пар повторяются (координата b);
- Соответствие является инъективным, так как элементы b ÎВ имеют ровно по одному прообразу.
- Данное соответствие не есть отображение, так как не является всюду определённым и функциональным.
Задача 3. Пусть A = R – множество действительных чисел, B = R+ - множество неотрицательных действительных чисел, G ={(x, y)ç x ÎR, y ÎR+, y = x 2 }. Найти тип этого соответствия.
Решение. Из свойств функции y = x 2 вытекает, что рассматриваемое соответствие:
1. Всюду определено, так как для каждого x ÎR найдется образ - значение y = x 2 ³ 0;
2. Сюръективно, ибо для каждого y ³0 найдется прообраз – значение 
;
3. Функционально, потому, что для каждого x ÎR найдется только один образ - значение y = x 2 ³ 0;
4. Не инъективно, так как для всякого y ÎR+, y > 0 во множестве R существуют два прообраза - значения x 1 = y, x 2 = − y;
5. Не взаимно однозначно, поскольку не является инъективным.
братное соответствие
Пусть задано некоторое соответствие G Í А´В = {(a, b)ç a ÎA, b ÎB, (a, b)ÎG}. Обратным по отношению к данному называется соответствие G─1 Í В´А = {(b, a)ç a ÎA, b ÎB, (a, b)ÎG}. Переход от G к G─1 осуществляется перестановкой первой и второй координат графика соответствия. В этом случае образ соответствия G становитсяпрообразом для G─1 , а прообраз для G – образом для G─1.
Графически обратное соответствие получается из прямого изменением направления стрелок.
Функциональное соответствие называется обратимым, если и обратное ему соответствие также будет являться функциональным. Обращение функционального соответствия возможно тогда и только тогда, когда оно является биективным.
Задача 1. А = { a, b, c, d }; B = {1, 2, 3, 4, 5}; G = {(a,2), (b,1), (b,5), (d,3)}. Определить тип прямого и обратного соответствий.
Решение. Обратное G─1={(2, a), (1, b), (5, b), (3, d)}.
Прямое соответствие G является частично определённым, не сюръективным, не функциональным (элемент b имеет два образа) и инъективным.
Обратное G─1 также есть частично определённым и не сюръективным, но является функциональным, но не инъективным (элемент b имеет два прообраза).
Задача 2. А = { a, b, c,}; B = {1, 2, 3}; G = {(a,1), (с,3), (b, 2)}. Определить тип прямого и обратного соответствий.
Решение. G─1 = {(1, a), (3, с), (2 ,b) }. Прямое и обратное соответствия являются биективными.
Задачи для самостоятельного решения.
1. Найти типы прямого и обратного соответствий:
a) G = {1, a), (1, b), (2, a)}; A = {1, 2}, B = { a, b };
b) G = {1,4), (2,3), (3,2), (4,1)}; A = B = {1, 2, 3, 4};
c) G = {(a 1, b 1), (a 2, b 2), (a 3, b 2)}; A = { a 1, a 2, a 3}, B = { b 1, b 2, b 3}.
ункция
Функции – это частный случай бинарных соответствий, на которые наложены дополнительные ограничения. Это понятие является основополагающим в математике.
Под функцией из множества Х в(на) множество Y мы понимаем всюду определённое бинарное соответствие, при котором каждый элемент множества Х связан с единственным элементом множества Y. Другими словами, для каждого х ÎХ существует ровно одна пара из соответствия вида (х, у). Графически (в стрелочном представлении) из каждого кружочка, представляющего элемент х,выходит ровно одна стрелка.
Для обозначения функции применяется такая символика: если f Í X´Y, то f: X®Y. При этом важно подчеркнуть, что функция f переводит элементы из Х в элементы из Y. Множество Х принято называть областью определения, а Y – областью значения функции.
Множеством значений функции называется подмножество в Y, состоящее из образов всех элементов х ÎХ. Оно обозначается символом f (Х).
Поскольку для каждого х ÎХ существует единственным образом определённый y ÎY, такой, что (х, у) Î f, мы будем писать у = f (x) и говорить, что функция f отображает множество Х в множество Y, а f (x) будем называть образом х при отображении f или значением функции, соответствующей аргументу х.
Если множества Х и Y бесконечны, мы не можем нарисовать стрелочное представление этого соответствия. В этом случае необходимо обратиться к традиционному математическому представлению такой функции, а именно, к её графику.
Рассмотрим важнейшие свойства функции. Функция называется инъективной или инъекцией, если из равенства f (х 1) = f (х 2) следует, что х 1 = х 2 для всех х 1, х 2 Î Х. Логически это эквивалентно тому, что из неравенства х 1 ≠ х 2 вытекает неравенство f (х 1) ≠ f (х 2). То есть у инъективной функции нет повторяющихся значений.
Функция называется сюръективной или сюръекцией, или функцией «на», если множество её значений совпадает с областью значений. Это означает, что для каждого у *ÎY найдётся такой х *ÎХ, что у * = f (х *). Таким образом, каждый элемент области значений будет являться образом какого-то элемента из области определения f.
Функция называется биективной или биекцией, если она инъективна и сюръективна одновременно.
Поскольку любая функция – это бинарное соответствие f: X®Y, поэтому всегда можно построить обратное соответствие. Если при этом мы снова получим функцию, то исходную функцию будем называть обратимой. Обратную функцию будем обозначать: f ─1 : Y®X.
Функция f состоит из пар вида (х, у), где у = f (x). Обратная функция f ─1 будет состоять из пар (у, х), где х = f ─1 (у). Иными словами, обратная функция «переворачивает» действие исходной.
Функция обратима тогда и только тогда, когда она биективна.
Задача 1. Какие из следующих соответствий есть функции, а какие нет и почему?
A = { a, b, c }, B = {1, 2, 3}.
a) G1 = { a,1), (b,1), (c,2)}
b) G2 = {(a,1), (b,2), (b,3), (c,2)}
c) G3 = {(a,1), (c,2)}.
Решение. G1 – это функция; G2 – не функция, так как элементу b соответствуют два различных элемента из Y – 2 и 3; G3 – не функция, потому что соответствие не является полностью определённым.
Задача 2. Определить, какие из изображенных функций инъективны, сюръективны или
биективны.
 |
|
|
Решение.
a) Данная функция не инъективна, поскольку значение 1ÎY соответствует а и b ÎX. Функция не является сюръекцией, потому что в элемент 2ÎY ничего не переходит.
b) Данная функция инъективна, так не имеет повторяющихся значений. Она также и сюръективна, поскольку множество её значений совпадает с областью значений. В этом случае имеем биективную функцию.
c) Значение 1 функция принимает как на а, так и на b. Значит, она не инъекция. Однако она сюръективна, поскольку в множество её значений входят все элементы области значений.
d) Функция инъективна, но не сюръективна.
Задача 3. Показать, что функция k: R®R, заданная формулой k (x) = 4 x + 3 является биекций.
Решение. В этой задаче множества Х и Y равны множеству действительных чисел R. Предположим, что существуют значения х = а 1 и х = а 2 такие, что k (a 1) = k (a 2), то есть
4 а 1 + 3 = 4 а 2 + 3.
Из этого равенства вытекает, что 4 а 1 = 4 а 2 , откуда следует, что а 1 = а 2. То есть разным значениям аргумента х соответствуют разные значения функции k (x). Значит, данная функция инъективна.
Покажем, что функция сюръективна. Для этого нужно доказать, что область значений функции совпадает с её множеством значений. Пусть у = b ÎY. Найдётся ли такое значение х = а ÎХ, что k (a) = b? Имеем: 4 а 1 + 3 = b. Откуда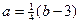 
. Очевидно, что это значение принадлежит множеству Х. Итак, данная функция сюръективна.
Поскольку k (x) = 4 x + 3 является одновременно и сюръективной, и инъективной, то она биективна.
Задача 4. Найти функцию, обратную к заданной формулой k (x) = 4 x + 3.
Решение. Поскольку в предыдущей задаче доказана биективность данной функции, следовательно она является обратимой. То есть если у = k (x), следовательно, существует функция х = k ─1(у). Из равенства у = 4 x + 3 выразим 
. Это и есть k ─1(у). однако по традиции в математике аргумент обозначается символом х, функция у. Перейдя к таким обозначениям, получим обратную функция в виде: 
.
График прямой и обратной функций симметричны относительно биссектрисы 1 и 3-го координатных углов (прямая у = х).
Задачи для самостоятельного решения.
1. Х = {0, 2, 4, 6}, Y = {1, 3, 5, 7}. Какие из следующих соответствий между множествами Х и Y являются функциями, определёнными на Х со значениями в Y? Какие из найденных функций инъективны, сюръективны?
a) {(6, 3), (2, 2), (0, 3), (4, 5)};
b) {(2, 3), (4, 7), (0, 1), (6, 5)};
c) {(2, 4), (4, 5), (6, 3)};
d) {(6, 1), (0, 3), (4, 1), (0, 7), (2, 5)}.
2. Области определения и значений следующих функций совпадают с множеством целых чисел Z. Какие из них инъективны, сюръективны или биективны?
a) f (n) = 2 n + 1;
b) 
c) 
3. Изобразить графики функций. Найти их множество значений. Какие из них инъективны, сюръективны или биективны. Найти обратную функцию (если возможно).
a) f: Z ® Z, f (x) = x 2 + 1;
b) f: N ® N, f (x) = 2 x ;
c) f: R ® R, f (x) = 5 x - 1;
d) f: R ® R, 
e) f: R ® R, f (x) = 2 x - | x |.
4. Функция f: Х ® Y задана формулой f (x) = 1 + 2/ х, где Х – множество вещественных чисел, отличных от 0, а Y – множество вещественных чисел без 1. Показать, что эта функция биективна и найти её обратную к ней функцию. Сделать чертёж.
