Пусть задано некоторое множество А. Количество элементов данного множества называется его мощностью и обозначается символом ç А ç. Очевидно, что пустое множество имеет мощность, равную нулю, то есть çÆç= 0.
Как могут меняться мощности множеств при операциях, производимых над ними? Точного ответа на этот вопрос нет, так как всё будет зависеть от взаимного расположения множеств.
Рассмотрим три возможных случая расположения двух непустых множеств А и В.
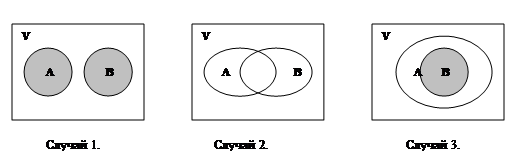
Рассмотрим множество, равное объединению А È В. Какова же будет его мощность в каждом из возможных трёх случаях.
Случай 1. Множества не пересекаются, то есть çАÇВç= 0. Тогда çАÈВç£ çАç + çВç. Иными словами, мощность объединения (суммы) множеств не превышает суммы их мощностей (нельзя исключать того, что А и В могут включать одинаковые элементы).
Случай 2. Множества пересекаются. Тогда çАÈВç= çАç + çВç- çАÇВç, то есть мощность объединения двух пересекающихся множеств равна сумме их мощностей без мощности их общей части (их пересечения).
Эта формула носит название формулы включений и исключений. С её помощью можно вычислить мощность любого множества.
Случай 3. Множество В включено в множество А, то есть имеет место включение В Ì А. Очевидно, что здесь çАÈВç = çАç, то есть мощность объединения подмножества и множества будет равно мощности самого множества. В случае, если А Ì В, то çАÈВç = çВç.
Обобщая эти три случая, получаем для объединения: çАç £ çАÈВç £çАç + çВç
Рассмотрим множество, равное пересечению А Ç В. Какова же будет его мощность в каждом из возможных трёх случаях.
Случай 1. çАÇВç = çÆç = 0.
Случай 2. çАÇВç = çАÈВç- çАç- çВç.
Случай 3. çАÇВç = çВç.
Обобщая эти три случая, получаем для пересечения: 0 £ çАÇВç £ çВç.
Рассмотрим множество, равное дополнению множества А. Поскольку Ā = V\А, то çĀç = çVç - çАç.
Рассмотрим множество, равное разности А \ В.
Случай 1. Здесь А\В = А, тогда и çА\Вç = çАç.
Случай 2. çА¸Вç = çА\Вç + çВ\Аç = çAÈBç - çBç.
Случай 3. çА\Вç = çAç - çВç.
Рассмотрим множество, равное симметрической разности А ¸ В.
Случай 1. Здесь А¸В = АÈB, тогда и çА¸Вç = çАÈBç.
Случай 2. çА¸Вç = çА\Bç + çВ\Aç = çAç + çBç -2çAÇBç= 2çAÈBç - (çAç + çBç).
Случай 3. Здесь А¸В = А\В, поэтому çА¸Вç = çAç - çВç.
Задача 5.1. А = {1, 2, 3, 4, 5}; B = {4, 5, 6, 7}. Найти мощности указанных множеств.
Решение. çAç = 5, çBç = 4, AÇB = {4, 5}, çAÇBç = 2, тогда çAÈBç= çАç + çВç- çАÇВ| = 5 + 4 – 2 = 7.
A\B = {1, 2, 3}, |A\B| = |A| - |AÇB| = 5 – 2 = 3. B\A = {6, 7}, |B\A| = |B| - |AÇB| = 4 – 2 = 2.
A¸B = {1, 2, 3, 6, 7}, |A¸B| = çА\Вç - çВ\Аç = 3 + 2 = 5.
Задача 5.2. В одном канадском городе жители говорят на английском и французском языках. На английском говорят 90% жителей, на французском – 80%. Сколько процентов жителей города говорят на обоих языках и на одном языке?
Решение. Пусть множество А – множество говорящих по-английски, В – говорящих по-французски. Тогда А\В – это множество жителей, которые говорят только по-английски, В\А – по-французски, а АÇВ – на обоих языках. АÈВ – это множество всех жителей города.
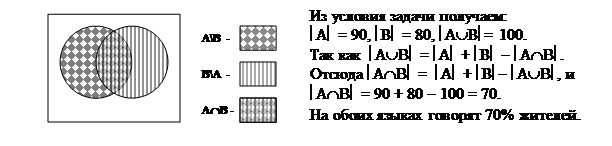
На одном английском говорят çA\Вç= çAç- çAÇBç= 90 - 70 = 20 процентов, только на французском çB\Аç= çBç- çAÇBç = 80 - 70 = 10 процентов жителей.
Задача 5.3. В отряде из сорока ребят 30 умеют плавать, 27 умеют играть в шахматы и только пятеро не умеют ни того, ни другого. Сколько ребят умеют плавать и играть в шахматы?
Решение. Пусть А – множество умеющих плавать, В – множество играющих в шахматы. Универсальное множество V – это весь отряд. Те же, кто не умеет ни того, ни другого – это множество, равное дополнению к АÈВ или V\(АÈВ). Имеем: çАç=30, çВç=27, çVç=40, çV\(AÈBç=5.
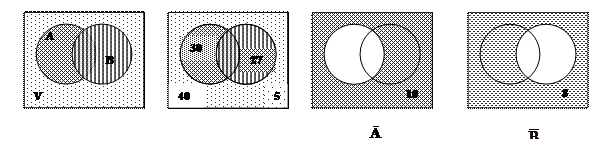
çĀç= çVç-çAç=40-30=10 – это те, кто не плавает (играет в шахматы или ничего не умеет);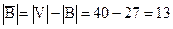 
- это те, кто не играет в шахматы (плавает или ничего не умеет). Те, кто только играет в шахматы - множество В\А мощностью 10-5=5, множество А\В – это умеющие плавать. Их количество равно 13-5=8.Так как çV\(AÈBç=çVç-çAÈBç=5, отсюда çAÈBç=çVç-5=40-5=35. По формуле включений и исключений çАÈВç= çАç + çВç- çАÇВç получим, что 35=5+8-çАÇВç, откуда çАÇВç=22.
Задача 5.4. Из 100 деталей на первом станке обработано 42 штуки, на втором – 30, на третьем – 28 шт. При этом на первом и втором станках обработано всего 5 деталей, на первом и третьем – 10, на втором и третьем – 8. На всех трёх станках обработано 3 детали.
Сколько деталей обработано на первом станке и сколько деталей не обработано ни на одном станке?
Решение. Пусть А – множество деталей, обработанных на 1-м станке; В – на 2-м; С – на 3-м. Универсум V – множество всех деталей в задаче. Очевидно, что |V| = 100, |A| = 42, |B| = 30, |C| = 28.
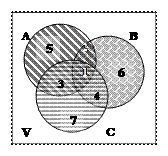
Метка 1 соответствует множеству АÇВÇС – это детали, обработанных хотя бы на одном станке (либо на одном, либо на двух, либо на трёх). Мощность его çАÇВÇСç = 3.
Метки 1 и 2– детали, обработанные на 1 и 2-м станках. Это множество АÇВ. Его мощность по условию çАÇВç= 5.
Метки 1 и 3 – детали, обработанные на 2-м и 3-м станках, множество АÇС, çАÇСç= 10, а
метки 1 и 4 – на 2-м и 3-м станках, множество ВÇС, çВÇСç= 8.
Метка 2 соответствует множеству деталей, которые обработаны только на 1-м и 2-м станках. Это множество (АÇВ)\С, мощность которого находим так: çАÇВç-çАÇВÇСç=
= 5-3=2.
Метка 3 – детали, обработанные на 1-м и 3-м станках. Это множество (АÇС)\В, мощность которого равна çАÇСç- çАÇВÇС ç= 10-3=7.
Метка 4 - множество деталей, обработанных на 2-м 3-м станках. Это множество (ВÇС)\А. Его мощность çВÇСç- çАÇВÇСç= 8-3=5.
Детали, которые обрабатывались только на одном первом станке – множество с меткой 5, равное разности множества А и множеств с метками 1, 2 и 3. Мощность этого множества (метка 5) равна çАç-(çм.1ç+çм.2ç+çм.3ç) = 42-(3+2+7) = 30.
Множество с меткой 6 - детали, обработанные только на втором станке. Его мощность равна çВç-(çм.1ç+çм.2ç+çм.4ç) = 30-(3+2+5) = 20.
Множество с меткой 7 - детали, обработанные только на третьем станке. Его мощность равна çСç-(çм.1ç+çм.3ç+çм.4ç) = 28-(3+7+5) = 13.
АÈВÈС – множество всех обработанных деталей. Его мощность можно найти как сумму мощностей всех семи множеств: çАÇВÇСç = 3+2+7+5++30+20+13 = 80.
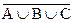- множество всех необработанных деталей. Его мощность вычислим так:
.
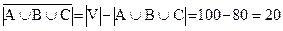Итак, на 1-м станке обработано 30 деталей, вообще не обрабатывалось – 20 деталей.
Задачи для самостоятельного решения.
1. В классе 40 учеников. 30 из них могут плавать, 27 – играть в шахматы, а пятеро не умеют ни того, ни другого. Сколько учеников могут плавать и играть в шахматы? (ответ:22).
2. На протяжении недели в кинотеатре демонстрировались фильмы А, В и С. Из 40 учеников каждый посмотрел либо все три фильма, либо только один из трёх. Фильм А посмотрели 13 человек, фильм В – 16, фильм С – 19. Сколько учеников посмотрели все три фильма? (ответ: 3).
6. Булеан множества. Разбиение множества.
Пусть задано непустое множество А. Множество всех подмножеств этого основного множества, включая его самое и пустое, называется булеаном данного множества. Обозначается Р(А) или 2х. Если А содержит n элементов, то булеан содержит 2 п элементов, которыми есть подмножества множества А, собственные и несобственные.
Среди элементов булеана есть как пересекающиеся, так и непересекающиеся подмножества. Рассмотрим лишь непересекающиеся, то есть такие, что Х i Ç X j = Æ. Если при этом А = Х1 È Х2 È …ÈХ n, то в этом случае множества Х1, Х2,… Х п называются блоками разбиения множества А. Для мощностей множеств имеет место условие: ç А ç£ ç Х1 ç +ç Х2 ç+…+ç Х п ç.
Задача 6.1. Найти булеаны множеств А ={1, 2}; B ={ a, b, c }; C ={1, 2, 3, 4}.
Решение. Р(А) = {{1}, {2}, {1, 2}, Æ};
P(B) = {{ a }, { b }, { c }, { a, b }, { a, c }, { b, c }, { a, b, c }, Æ};
P© = {{1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}, {1, 2, 3}, {1, 2, 4},
{1, 3, 4}, {2, 3, 4}, {1, 2, 3, 4}, Æ}.
Задача 6.1. Найти разбиение множеств А ={1, 2}; B ={ a, b, c }; C ={1, 2, 3, 4}.
Решение. Множество А: Х1 = {1}, X2 = {2}; A = X1 È X2. Это единственный способ разбиения множества А.
Множество В: первый способ: Х1 = { a }, X2 = { b }; X3 = { c };
второй способ: Х1 = { a, b }, X2 = { c };
третийспособ: Х1 = { a }, X2 = { b, c }.
Множество С: первый способ: Х1 = {1}, X2 = {2}; X3 = {3}; Х4 = {4};
второй способ: Х1 = {1}, X2 = {2, 3}; X3 = {3};
третий способ: Х1 = {1, 2}, X2 = {2}; X3 = {3, 4};
четвёртый способ: Х1 = {1, 2}, X2 = {3, 4};
пятый способ: Х1 = {1, 2, 3}, X2 = {4}; и т.д.
Задачи для самостоятельного решения.
1. Найти булеаны следующих множества: А ={1}, B ={3, 5}, C ={7, 8, 10}, D ={ m, n, p, q }.
2. Найти разбиение множеств A, B, C, D.
7. Декартово произведение множеств. Понятие упорядоченного множества.
Пусть А и В – некоторые непустые множества, где а Î А, b Î В. Рассмотрим двухэлементное множество, состоящее из пар а и b. Пара (или двойка) { a, b } называется неупорядоченной. Здесь порядок записи элементов не важен, поэтому { a, b } = { b, a }. Пара (a, b) называется упорядоченной. Здесь порядок записи существенен, поэтому (a, b) ¹ (b, a).
Множество, для которого имеет значение порядок записи его элементов, называется упорядоченным. В противном случае – неупорядоченным.
Декартовым (или прямым) произведением множеств А и В называется множество всех упорядоченных пар, где первый элемент принадлежит множеству А, а второй – В.
А´В = {(a, b) ç a ÎA, b ÎB}
Операция прямого произведения множеств обобщается на любое конечное число множеств и записывается в виде:
А1 ´А2 ´…´ А n = {(a 1, a 2, …, an) ç a 1ÎA1, a 2ÎA2,…, an ÎA n }
Упорядоченные элементы этого произведения (a 1, a 2, …, an) называются векторами, последовательностями, кортежами или просто «энками».
Если декартово произведение выполняется на одном и том же множестве, то его называют декартовой степенью этого множества.
А1 ´А2 ´ … ´А п = А п
Мощность декартова произведения равна произведению мощностей сомножителей:
| А |= | А1 | ×| А2 | × … × | А n |
Декартово произведение обладает следующими свойствами:
1. некоммутативность: А´В ¹ В´А, если А ¹ В;
2. неассоциативность: (А´В) ´С ¹ А ´(В ´ С);
3. дистрибутивность относительно операций:
(А È В)´ С = (А ´ С)È(В ´ С),
(А Ç В)´ С = (А ´ С)Ç(В ´ С),
(А \ В)´ С = (А ´ С) \ (В ´ С),
(А È В)´ С = (А ´ С)È(В ´ С),
(А ¸ В)´ С = (А ´ С) ¸(В ´ С).
Для случая двух множеств декартово произведение можно иллюстрировать с помощью диаграммы Венна. Пусть А = { a 1, a 2,…, an }; B = { b 1, b 2,…, bm }.
 |
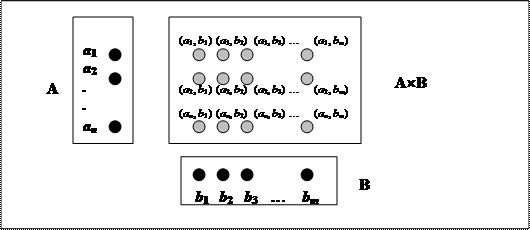Рассмотрим прямое произведение множества R действительных чисел самое на себя. Множество R ´ R или R2 состоит из всех упорядоченных пар вещественных чисел (х, у). Их можно трактовать как координаты точек плоскости XOY, то есть декартовой плоскости. Часто в дискретной математике множество вещественных чисел обозначают D (вместо R). Смысл этого обозначения станет понятным из дальнейшего изложения.
Задача 7.1. Найти декартово произведение А´В и В´А на множествах А ={1, 2} и B ={ a, b, c }.
Решение. А´В = {1, 2}´ { a, b, c } = {(1, a), (1, b), (1, c), (2, a), (2, b), (2, c)};
B´A = { a, b, c } ´ {1, 2} = {(a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2)}.
Задача 7.2. Найти декартовы степени А 2, А 3, В 2.
Решение. А2 = А´А = {1, 2}´{1, 2} = {(1,1), (1,2), (2,1), (2,2)};
A3 = A´A´A = A2 ´A = {1, 2}´{1, 2}´{1, 2} = {(1,1), (1,2), (2,1), (2,2)}´ {1, 2} =
{(1,1,1), (1,1,2), (1,2,1), (1,2,2), (2,1,1), (2,1,2), (2,2,1), (2,2,2)};
B2 = B´B = { a, b, c }´{ a, b, c } = {(a, a), (a, b), (a, c), (b, a), (b, b), (b, c), (c, a), (c, b), (c, c)}.
Задача 7.3. Найти геометрическую интерпретацию множеств:
a) [1, 4] ´ [2,3];
b) [1, 2]2;
c) [1, 2]3.
Решение.
a) Пусть А ={ x ô1£ x £4}, B = { у ô2£ у £3}. Отложим на оси ОХ множество А, а множество В – на оси OY. Совершенно ясно, что множества А и В содержат бесконечное множество элементов. Их произведение А´В={(x, y)ô x ÎA, y ÎB} есть множество точек прямоугольника с вершинами в точках (1,2), (1,3), (4,2) и (4,3).
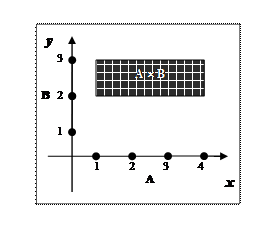
b) Множество [1,2]2 = [1,2] ´ [1,2] – это множество точек квадрата с вершинами в точках (1,1), (1,2), (2,1), (2,2).
c) Множество [1, 2]3 - это множество точек куба с вершинами в точках (1,1,1), (1,1,2), (1,2,1), (1,2,2), (2,1,1), (2,1,2), (2,2,1), (2,2,2).
Задача 7.4. Проверить справедливость равенства С ´(В \ А)=(С ´ В)¸(С ´(А Ç В)) для множеств А ={ a, d }, B ={ b, d }, C ={ c }.
Решение. Найдём множество в левой части равенства:
В\А = { b, d }\{ a, d } = { b }; C´(B\A) = { c }´{ b } = {(c, b)};
Аналогично находим множество в правой части равенства:
С´В = { c }´{ b, d } = {(c, b), (c, d)}; AÇB = { a, d } Ç { b, d } = { d };
C´(AÇB) = { c }´{ d } = {(c, d)}; (С´В)¸(С´(АÇВ)) = {(c, b), (c, d)}¸ {(c, d)} = {(c, b)};
В левой и правой части равенства имеем одно и то же множество. Следовательно, для данных множеств равенство справедливо.
Задача 7.5. Доказать, что (А È В)´ С = (А ´ С)È(В ´ С).
Решение. Воспользуемся определением равенства множеств. Ясно, что мы имеем дело с множествами, состоящими из упорядоченных пар. Пусть элемент (х, у)Î(АÈВ)´С, откуда имеем, что х Î(АÈВ), у ÎС. Значит х ÎА или х ÎВ, а тогда (х, у)ÎА´С или (х, у)ÎВ´С. Мы показали, что всякий элемент, принадлежащий множеству слева принадлежит также и множеству справа, то есть (АÈВ)´С Í(А´С)È(В´С).
Пусть теперь (х, у) Î (А´С)È(В´С). Отсюда вытекает, что (х, у)Î(А´С) или что
(х, у)Î(В´С). В первом случае х ÎА, у ÎС, во втором - х ÎВ, у ÎС. Следовательно, х ÎАÈВ, а (х, у)Î(АÈВ)´С. Итак, (А´С)È(В´С) Í(АÈВ)´С. Что и доказывает наше равенство.
Задачи для самостоятельного решения.
1. Найти декартово произведение А´В и В´А на множествах
a) А ={2, 4} и B ={3, 5, 7};
b) A ={ k, m } и B ={ m, n, l }.
2. Найти декартовы степени А 2, А 3, если А ={ a, b, c }.
3. Проверить справедливость равенства С ´(A È B)=(С ´ A)È(С ´(B \ A)) для множеств А ={1, 2}, B ={2, 3}, C ={1, 3}.
4. Доказать, что
a) если В Ì А и С Ì А, то (В ´ С)Ì(А ´ А); b) A´ (B Ç C) = (A ´ B)Ç(A ´ C).
Литература
- Міхайленко В.М., Федоренко Н.Д., Демченко В.В., Дискретна математика. – Київ.:Видавництво Європейського університету, 2003.- 317с.
- Мельников В.Н., Логические задачи. – Киев – Одесса.: Вища школа, 1989. -344с.
- Остапович М.В., Чернишенко С.В., Ротар О.А., Дискретна математика для інформатиків.- Дніпропетровськ.: видавництво ДНУ, 2008. – 183с.
- Тишин В.В., Дискретная математика в примерах и задачах. – С.-Петербург.:БХВ-Петербург, 2008. – 354с.
- Хаггарти Р., Дискретная математика для программистов. – Москва.: Техносфера, 2005. – 400с.
- Балюкевич Э.Л., Ковалёва Л.Ф., Романников А.Н., Дискретная математика. - Москва.: Московский государственный университет экономики, статистики и информатики, 2007. – 125с.
- Шевелёв Ю.П., Дискретная математика. – Томск.: Томский государственный университет систем управления и радиоэлектроники, 2003. – 118с.
- Кулабухов С.Ю., Дискретная математика. – Шахты.: Южно-российский государственный университет сервиса, 2006. – 150с.
- Интернет-университет информационных технологий, видеокурс по основам дискретной математики.: www.INTUIT.ru
