пособы задания множеств
Существует несколько способов задания множеств.
a) Вербальный (словесный), то есть с помощью описания характеристических свойств, которыми должны обладать элементы множества;
b) Задание списком (перечислением) всех элементов множества. Данный способ применим лишь к конечным множествам.
c) Описанием ограничивающего свойства – характеристическим предикатом, то есть указанием тех свойств p (x), которыми должны обладать элементы данного множества и не обладают элементы других множеств.
d) Геометрический способ задания – с помощью графиков или диаграмм. Этот способ применим как к конечным, так и бесконечным множествам.
e) Задание с помощью порождающей процедуры f, то есть указать правило, по которому формируются элементы данного множества.
Множества обозначаются большими латинскими буквами (например А, В, Х, Y и т.д.), а элементы этих множеств – малыми буквами (например a, b, x, y). Факт принадлежности некоторого элемента данному множеству символически записывается так: а Î А и читается: «Элемент а принадлежит множеству А».
Задача 1.1. Выяснить, каким способом заданы следующие множества и перечислить все элементы этих множеств:
a) { x ô x есть делитель числа 100};
b) { x ô x есть простой делитель числа 100};
c) { x ô x есть простой множитель числа 100};
d) { x ô x ÎN; x 2 – 1 = 0 и x 2 – 4 = 0};
e) { x ô x есть буква слова «академия»};
f) { x ô x ÎN; 2log4 x = 1};
g) { x ô x ÎN;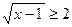 
}.
Решение.
a) Данное множество состоит из всех делителей числа 100, то есть в него включаются лишь те числа, которые делят число 100 нацело. Очевидно, что налицо задание множества с помощью характеристического предиката «быть делителем числа 100». Перечислим все эти числа: 2, 4, 5, 10, 20, 25, 50. Добавив сюда число 1 и самое 100, получим искомое множество. Обозначим его А. Тогда А = {1, 2, 4, 5, 10, 20, 25, 50};
b) Множество задано с помощью характеристического предиката «быть простым делителем числа 100». Среди делителей предыдущей задачи отберём лишь простые числа, которыми будут 2 и 5. Все же остальные делители являются составными. Число 1 как известно из курса школьной арифметики, не относится ни к простым, ни к составным числам. Обозначив это множество В, получим: В = {2, 5};
c) Множество задано с помощью характеристического предиката «быть простым множителем числа 100». Разложим 100 на простые множители. Получим следующее тождество: 100 = 2×2×2×5. Эти числа и будут элементами искомого множества, которое обозначим С = {2, 2, 5, 5}. Ответ можно было бы оставить в таком виде, однако в теории множеств количество одинаковых элементов, как правило, игнорируется. Поэтому будет корректнее ответ представить в виде: С = {2, 5};
d) Данное множество можно считать заданным с помощью порождающей процедуры, которой является процедура решения квадратных уравнений и отбора корней по признаку принадлежности их к множеству натуральных чисел. Однако, справедливости ради, следует отметить, что часто при определении способа задания множества бывает достаточно трудно утверждать, что множество задано этим и только этим способом. В данном примере вполне можно утверждать, что способ задания множества – с помощью характеристического предиката «отбор корней уравнения по признаку принадлежности к множеству N». Решаем оба уравнения:
x 2 – 1 = 0, его корни +1 и -1; x 2 – 4 = 0, его корни +2 и -2. Поскольку числа -1 и -2 не являются натуральными, искомое множество, которое мы обозначим D, будет таким: D = {1, 2};
e) Способ задания – с помощью характеристического предиката. Обозначим множество Е. Получим: Е = {а, к, д, е, м, и, я}, где буква «а» упомянута лишь один раз;
f) Способ задания данного множества аналогичен примеру d). Решим данное показательно-логарифмическое уравнение 2log4 x = 1. ОДЗ данного уравнения – все х ³0. 2log4 x = 20, откуда log 4 x = 0, корень х = 1. Это натуральное число. Значит, наше множество, которое обозначим через F, будет состоять из одного лишь элемента:
F = {1};
g) Способ задания данного множества аналогичен примеру d). Решаем данное иррациональное неравенство 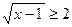. ОДЗ – все х ³ 1. Обе части возведём в квадрат: х – 1 ³ 4, откуда х ³ 5. Это не противоречит ОДЗ, поэтому область решения данного неравенства х ³ 5. Другими словами х Î [5; ¥]. Очевидно, что натуральных чисел на данном интервале будет бесчисленное множество. Поэтому данное множество G будет бесконечным: G = {5, 6, 7, … n,… }.
Задача 1.2. Записать множества с помощью свойства р (х):
a) {2, 3, 11};
b) {1, 3, 9, 27, 81, 243}
c) {s, t, u, d, e, n}
Решение.
a) Подобрать характеристический предикат можно, например, так. Перемножим все числа. Получим: 2×3×11 = 66. Тогда А = { a ô a – простой делитель числа 66};
b) Все представленные числа являются степенями числа 3 (30=1, 31=3, 32=9 и т.д.). Поэтому множество В можно задать с помощью свойства:
В = { b ô b – степень числа 3 с показателем от 0 до 5};
c) C = { c ô c – буква слова «student»}.
Задача 1.3. Изобразить следующие множества графически:
a) А = {(x, y)ô x ÎR, y ÎR; x 2 + y 2 £ 4};
b) B = {(x, y)ô x ÎR, y ÎR; x + y >0, x + y – 2 £ 0};
c) C = {(x, y)ô x ÎR, y ÎR; | x | £ 1 и | y + 2| £ 4};
d) D = {(x, y)ô x ÎR, y ÎR и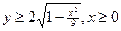 
};
e) E = {(x, y)ô x ÎR, y ÎR и y £ |sin x |};
f) F = {(x, y)ô x ÎR, y ÎR и x 2 = y 2 }.
Решение. Все заданные множества состоят из пар действительных чисел, которые удовлетворяют некоторым условиям. Изображая точки, соответствующие данным парам в декартовой системе координат на плоскости, получим некоторые области, которые и будут геометрическим (графическим) изображением исследуемого множества.
a) Построим границу множества А. Для этого от неравенства перейдём к равенству:
x 2 + y 2 = 4. Из курса аналитической геометрии известно, что это уравнение есть уравнение окружности с центром в начале координат и радиусом 2. Она и будет являться границей множества. Далее следует выяснить, какую часть плоскости нам следует выбрать: ту, что лежит внутри окружности либо ту, что лежит извне. Для этого зададимся координатами какой-либо точки, которая явно находится в выбранной области. Например, точка начала координат О(0;0). Подставим значения х = 0 и у = 0 в неравенство x 2 + y 2 £ 4. Получим: 02 + 02 £ 0, то есть в точке О (0;0) данное неравенство справедливо. Следовательно, нам нужно выбрать часть плоскости внутри окружности. Если взять координаты других точек внутри окружности и подставить их в неравенство, результат будет таким же. Напротив, для точек извне неравенство будет ложным. Например, точка Q(10;10): 102 + 102 = 200, а это никак не меньше 0! Подытоживая всё сказанное, можем утверждать, что множество А – это круг радиуса 2 с центром в начале координат.
b) Для построения границ множества В рассмотрим равенства: x + y =0, x + y – 2 = 0. Первая прямая (её уравнение можно записать как у = - х) есть биссектриса 2-го и 4-го координатных углов. Она разделяет координатную плоскость на две части: ту, которая лежит выше (или правее) прямой и ту, которая ниже (или левее) прямой. Чтобы выбрать нужную часть, возьмем пробную точку с координатами, например, Q(10;10) и подставим её координаты в неравенство x + y > 0. Получим: 10 +10 > 0 то есть неравенство справедливо для части плоскости выше (правее) прямой
x + y =0. Вторая прямая (её уравнение x + y – 2 = 0 может быть записано в отрезках на осях 
) отсекает на обеих осях отрезки длиной по 2 единицы и проходит параллельно первой прямой через 2-й, 1-й и 3-й квадранты. Она также разделяет координатную плоскость на две части: одна выше (правее) и вторая ниже (левее). Для выбора нужной нам части можно использовать, например, точку О(0;0). Подставляем х = 0 и у = 0 в неравенство x + y – 2 £ 0. Получим: 0 + 0 – 2 £ 0 - справедливо. Следовательно выбираем ту часть плоскости по отношению ко второй прямой, где лежит точка О(0;0). В итоге получаем область, координаты точек которой удовлетворяют обоим неравенствам (например, это точки (1;1), (0;1), (1;0); (2;-1) и т.д.),. Это полоса, лежащая между двумя параллельными прямыми, включая и точки, принадлежащие второй прямой (поскольку неравенство нестрогое). Данная область и определяет искомое множество В.
c) Неравенство | x | £ 1 эквивалентно двум: -1 £ х £ 1. Казалось бы, что это множество точек отрезка [-1; 1]. Если бы мы рассматривали множество из одного элемента, это было бы так. Однако наше множество С состоит из пар действительных чисел (х; у). Поэтому геометрически неравенство -1 £ х £ 1 представляет собой множество точек, лежащих внутри вертикальной полосы между прямыми х = 1 и х = -1. Неравенство | y + 2| £ 4 также эквивалентно двум: -4 £ y + 2 £ 4. Перенося 2 влево и вправо, получаем: -6 £ y £ 2. Геометрически это будет множество точек, лежащих внутри горизонтальной полосы между прямыми y = -6 и y = 2. Итак, мы получили две пересекающиеся полосы. Какую же часть необходимо выбрать для искомого множества С? В условии задачи оба неравенства соединены союзом «и». А это значит, что необходимо выбрать те точки из обеих полос, координаты которых одновременно удовлетворяют обоим неравенствам. В результате получаем прямоугольник. Это и есть наше множество С.
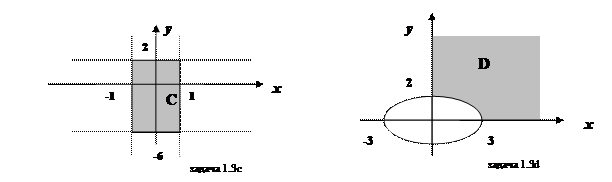
d) Рассмотрим неравенство 
. Чтобы оно стало «узнаваемым», возведём в квадрат левую и правую его части. Это можно сделать потому, что справа - неотрицательная величина арифметического корня. Слева величина у также неотрицательна, ибо в противном случае неравенство теряло бы всякий смысл. После возведения во вторую степень обеих частей и некоторого преобразования получаем: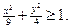 
Это неравенство описывает часть координатной плоскости, лежащей вне эллипса 
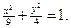Однако исходное неравенство имеет вид , причём, как было сказано, величина у неотрицательна. Значит, описываемая область будет включать лишь верхнюю часть координатной плоскости, лежащей вне эллипса. Рассмотрим последнее неравенство х ³ 0, которое описывает правую часть координатной плоскости. Сопоставляя все выкладки, получим множество точек, расположенных в первом квадранте вне эллипса. Это и будет искомое множество D.
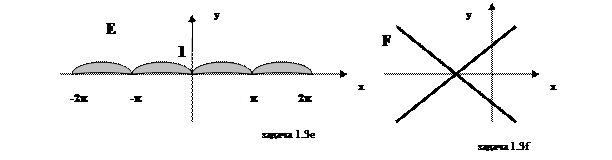
e) Построим график функции у = sin x, а затем ту его часть, которая находится ниже оси абсцисс, зеркально отразим на верхнюю полуплоскость. Получим график у = |sin x |. Неравенство же y £ |sin x | определит искомое множество Е, точки которого будут находиться между осью абсцисс и дугами отраженной вверх синусоиды.
f) В отличие от предыдущих задач здесь имеем равенство x 2 = y 2, которое, как известно, определяет некоторую линию. Для «узнавания» данной линии сделаем ряд тождественных преобразований: x 2 - y 2 = 0, (х – у) (х + у) = 0. Далее приходим к совокупности х – у = 0 и х + у = 0. Получаем пару пересекающихся прямых - биссектрис 1- 3-го и 2 – 4-го квадрантов. Множество F и представляет собой точки этих прямых.
Задачи для самостоятельного решения.
1. Перечислить все элементы следующих множеств:
a) { x ô x есть делитель чисел 6 и 8}; (ответ: 2)
b) { x ô x ÎN; x 3 - 5 x 2 + 4 = 0}; (ответ: 1)
c) { x ô x ÎR; x + 1/ x > 2; x > 0}; (ответ: х Î(0, ¥))
d) { x ô x – буква слова «университет»);
e) { x ô x ÎZ; sin x < 0; cos x > 0}; (ответ: -1).
2. Изобразить следующие множества графически:
a) { (x, y)ô y £ 2 x 2 };
b) { (x, y)ô y ³ | x | + 1};
c) { (x, y)ô x 2 + y 2 – 25 > 0}
ножество и подмножество
Универсальным (или фундаментальным) множеством называется множество, которое создано всеми элементами какого-либо определённого типа. Обозначается оно буквой V (или U) и читается «универсум».
Подмножество – это любая часть основного множества. При этом элементы подмножества обладают некоторым дополнительным свойством ра (х). Этот факт можно записать так: А = { x ô x Î V и ра (х)}.
Если свойство, задающее некоторое подмножество, противоречит свойству, по которому задаётся основное множество, то данное подмножество будет пустым, то есть не содержащим ни единого элемента. Обозначается оно символом Æ.
Выражение А Ì В (читается «А включено в В») означает, что множество А есть подмножество множества В. При этом все элементы, принадлежащие А,будут также принадлежать и В. Однако в множестве В могут найтись элементы, не принадлежащие А. В этом случае множество А называется собственным подмножеством множества В, а В, в свою очередь, называется надмножеством. Можно также рассматривать и выражение В É А, которое читается «В включает в себя А».
Равными считаются множества, состоящие количественно и качественно из одних и тех же элементов. Факт равенства множеств записывается так: А = В, неравенства А ¹ В.
Выражение А Í В обозначает включение в широком смысле, то есть А есть подмножество В. При этом не исключено, что А = В. Можно также рассматривать и выражение В Ê А.
Два множества А и В равны тогда и только тогда, когда А Í В, а В Í А.
Всякое пустое множество Æ считается частью любого множества (пустой его частью). Всякое непустое множество является частью себя самого, то есть А Í А (полная часть множества).
Полная и пустая части всякого множества образуют его несобственные подмножества. Все остальные подмножества данного множества являются собственными.
Рассмотрим множество, которое состоит из элементов некоторого множества А, причем элементы могут входить в это множество в произвольном количестве. Такое множество называется мультимножеством множества А и обозначается М(А).
Пример. А = {2, 4, 6}; M(A) = {2, 2, 2, 2, 4, 6, 6, 6}.
Здесь М(А) – это мультимножество множества А. С точки зрения теории множеств эти два множества не отличаются друг от друга, то есть А = М(А).
Мультимножество М(А) множества А можно задать самим множеством А = { a 1, a 2, … a n} со всеми различными элементами и спецификацией (n 1, n 2,… nk), где ni – число повторов элемента аi. В рассмотренном примере М(А) задаётся как А = {2, 4, 6} и спецификацией (4, 1, 3).
Задача 2.1. Дано универсальное множество V = {1,2,3,…20} – натуральные числа от 1 до 20. Найти следующие подмножества:
a) множество простых чисел;
b) множество делителей числа 20;
c) множество чисел, делящихся на 6;
d) множество квадратов чисел;
e) множество разностей предыдущего и последующего элементов универсума.
Решение.
a) множество простых чисел: А = {2, 3, 5, 7, 11, 13, 17, 19}. Очевидно, что А Ì V.
b) множество делителей числа 20: В = {1, 2, 4, 5, 10, 20}. Здесь также В Ì V.
c) множество чисел, делящихся на 6: С = {6, 12, 18}, C Ì V.
d) множество квадратов чисел: D = {1, 4, 9, 16}. По условию задачи D Ì V, имы должны рассмотреть лишь множество тех квадратов чисел, которые не выйдут за пределы универсума;
e) множество Е = { x 1- x 2; x 2- x 3; … x 19- x 20}. Совершенно очевидно, что полученное множество не есть подмножеством данного универсума. Иными словами, предикат, по которому оно формируется, противоречит предикату универсума. Таким образом Е Ë V, хотя по условию Е Ì V. Значит Е = Æ.
Задача 2.2. Среди следующих множеств указать равные: А = {3, 5, x, y }; B = {3, 2, 5, x, y }; C = { y, y, 5, 3, x, x }; D = {3, 4, 5, x, y }.
Решение. A = C, поскольку качественно оба множества состоят из элементов 3, 5, x и y. Количество элементов множества А равно 4. Множество В, на первый взгляд, содержит больше элементов. Однако среди них есть повторяющиеся: 2 раза х и столько же у. Для множества же неважно, сколько раз повторяется один и тот же элемент, важно лишь, чтобы элементы отличались друг от друга. Что же касается множеств B и D, то они не равны, так как содержат разные элементы. Можно лишь утверждать, что А Ì В, А Ì D, C Ì B и
C Ì D.
Задача 2.3. Будут ли равны между собой множества А и В и, если нет, то почему?
a) A = {1, (2, 5), 6}, B = {1, 2, 5, 6};
b) A = {1, {2, 5}, 6}, B = {1, {5, 2}, 6};
c) A = {1, {2, 7}, 6}, B = {1, (2, 7), 6};
d) A = Æ, B = { Æ };
e) A = {0}, B = { Æ }.
Решение.
a) A ¹ B. Разберём, почему. Множество В состоит из элементов 1, 2, 5 и 6. В отличие от А, элементами которого являются 1, 6 и упорядоченная пара чисел (2, 5). Элементы обоих множеств качественно различны. Поэтому эти множества и не равны.
b) А = В. Элементами множества А являются числа 1 и 6, а также подмножество
{2, 5}. Множество В также состоит из элементов 1 и 6, а также подмножества
{5, 2}. Очевидно, что подмножества {2, 5} и {5, 2} равны. Следовательно множества А и В состоят из одних и тех же элементов. Значит, они равны.
c) A ¹ B. Оба множества имеют одинаковые элементы 1 и 6. Однако элементом А является подмножество {2, 7}, а элементом В есть упорядоченная пара чисел (2, 7). Понятно, что это качественно различные элементы. Следовательно, множества не равны.
d) A ¹ B. Множество А – это пустое множество, не содержащее ни одного элемента. В состав же множества В входит один элемент, которым является пустое множество.
e) A ¹ B. Множество А имеет один элемент – это число 0. Множество В также состоит из одного элемента, которым является множество, в данном случае пустое. Это качественно разные элементы.
Задачи для самостоятельного решения.
1. Записать следующие утверждения, используя символы теории множеств:
a) множество S есть подмножество Т;
b) х принадлежит множеству Р;
c) множество Y не является подмножеством множества Х;
d) z не принадлежит множеству Z.
2. Заданы четыре множества: А = {1, 3, 5, 7}; B = {3, 5}; C = {2}; D = {5, 7, 9}. Какие из следующих утверждений являются истинными, а какие ложными?
a) В Ì А (ответ: верно);
b) Æ Î D (ответ: неверно, хотя пустое множество и включено в D, но не в качестве его элемента, а в качестве подмножества);
c) С Ì В (ответ: неверно);
d) В Ì D (ответ: неверно);
e) В Î А (ответ: неверно, хотя В и включено в А, но как подмножество, а не как элемент);
f) С Ë В (ответ: верно).
перации над множествами
Рассмотрим некоторое универсальное множество V и его подмножества А, В, С и т.д. Для наглядности будем изображать множества геометрически с помощью диаграмм Эйлера-Венна. При этом универсальное множество принято обозначать прямоугольником, а его подмножества – произвольными геометрическими фигурами (чаще всего кругами).
На множестве всех подмножеств универсума (включая пустое множество Æ и V) определим следующие операции: дополнение, объединение, пересечение, разность и симметрическую разность.
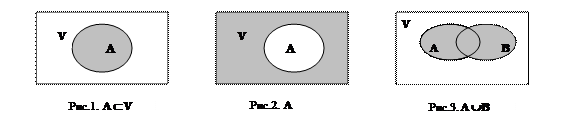
На рис.1 изображено множество А Ì V ( читается: А включено в V), то есть каждый элемент А есть также элементом универсума. Символически это можно записать так:
А = { x | x Î A и x Î V }.
Читается: множество А состоит их элементов х таких, что принадлежат А и V.
На рис.2 изображено множество Ā – дополнение множества А. Символически это записывается так:
Ā = { x | x Î V и х Ï А }.
Дополнением множества А называется множество, состоящее из всех тех и только тех элементов х из V таких, которые не принадлежат множеству А. Операция дополнения обладает свойствами:
1) 
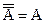- инволюция; 2) 
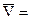Æ.
На рис.3 изображено объединение множеств. Объединением множеств А с В называется множество, состоящее из всех тех и только техэлементов х, которые принадлежат хотя бы одному из множеств А или В. А È В = { x | x Î A или x Î B }. Операция объединения множеств обладает свойствами:
1) А È А = А – идемпотичность;
2) А È (В È С) = (А È В) È С – ассоциативность;
3) А È В = В È А – коммутативность;
4) А È Æ = А, А È V = V;
5) А È Ā = V.
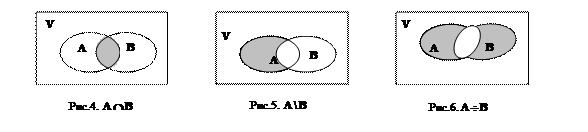
На рис.4 изображено пересечение множеств А и В. Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат как множеству А, так и множеству В.
А Ç В = { x | x Î A и х Î В }
Операция пересечения обладает свойствами:
1) А Ç А = А идемпотичность;
2) А Ç Ā = Æ;
3) А Ç (В Ç С) = (А Ç В) Ç С – ассоциативность;
4) А Ç В = В Ç А – коммутативность;
5) А Ç Æ = Æ; А Ç V = А.
На рис.5 изображена разность множества А и В. Разностью множества А и множества В называется множество, состоящее из тех и только тех элементов множества А, которые не принадлежат множеству В.
A \ B = { x | x Î A и x Ï B}
Разность множеств А и В, исходя из данного определения, можно также задать как А Ç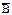 
.
На рис.6 изображена симметрическая разность множеств. Симметрической разностью множества А и множества В называется множество, состоящее из тех и только тех элементов, принадлежащих множеству А или множеству В, исключая элементы, принадлежащие обоим множествам одновременно.
A ¸ B = { x | x Î A и x Ï B или x Ï A и x Î B }
Данная операция обладает следующими свойствами:
1) А ¸ В = В ¸ А -коммутативность;
2) (А ¸ В) ¸ С = А ¸ (В ¸ С) – ассоциативность;
3) А ¸ Æ = Æ ¸ А – существование нейтрального элемента;
4) А ¸ А = Æ - существование симметрического элемента;
5) А Ç (В ¸ С) = (А Ç В) ¸ (А Ç С) – дистрибутивность относительно пересечения.
Симметрическая разность с помощью определенных ранее операций может быть представлена в виде: A ¸ B = (А \ В) È (В \ А) или A ¸ B = (А È В) \ (А Ç В).
Следует также отметить, что иногда эту операцию называют дизъюнктивной суммой и обозначают знаком Å или D.
Задача 3.1. Заданы множества: V = {2; 3; 4; 8; 9; 10; 11}; A = {2; 3; 4}; B = {3; 4; 8; 9} и
С = {2; 10; 11}. Найти следующие множества:
a) А È В; А È В È С;
b) Ā;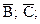 
c) А Ç В; В Ç Ā;
d) А \ В; В \ А; А \ С \ В;
e) А ¸ В; А ¸ С; (А ¸ В) ¸ С.
Решение.
a) По определению объединение А È В будет состоять из всех элементов обоих множеств, то есть А È В = {2; 3; 4; 8; 9}. Как мы помним, кратность элементов не учитывается.
Аналогично для нахождения А È В È С к элементаммножества А È В присоединим элементы множества С. Получим: А È В È С = {2; 3; 4; 8; 9; 10; 11}. Очевидно, что А È В È С = V.
b) Для нахождения дополнения к множеству А (множества Ā)выберем те элементы, которые принадлежат универсуму и не принадлежат А. Таковыми будут элементы 8, 9, 10 и 11. То есть Ā = {8; 9; 10; 11}.
Аналогично найдем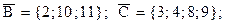 
c) Пересечение множеств – это множество, состоящее из их общих элементов. Для множеств А и В таковыми будут только два элемента – 3 и 4. Следовательно, можем записать: А Ç В = {3; 4}.
Аналогично найдём В Ç Ā = {3; 4; 8; 9} Ç {8; 9; 10; 11} = {8; 9}.
d) Для нахождения разности А \ В отберём только те элементы, которые принадлежать исключительно множеству А и не принадлежат В. Таковым будет только один элемент – 2. Значит, А \ В = {2}.
Аналогично найдём В \ А = {8; 9}.
A \ C \ B = (A \ C) \ В = {3; 4} \ {3; 4; 8; 9} = Æ.
e) Для нахождения симметрической разности А ¸ В сначала объединим эти множества, а затем из этого объединения удалим их общие элементы. Таких элементов буде два: 3 и 4. Следовательно, А ¸ В = {2; 8; 9}.
Аналогично, А ¸ С = {3; 4; 10; 11}.
(А ¸ В) ¸ С = {2; 8; 9} ¸ {2; 10; 11} = {8; 9; 10; 11}.
Задача 3.2. Заданы множества: V = { a; b; c; d; e; f; k, m, n }; P = { a; b; c, d }; Q = { b; c; e; f; k } и R = { k; m; n }. Выполнить следующие действия:
a)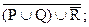 
b) 
c)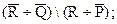 
d) 
e)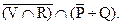 
Решение.
a) Сначала выполним действие в скобках и найдём объединение множеств P c Q:
P È Q = { a, b, c, d, e, f, k }.
Далее найдём дополнение к множеству R.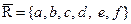 
. Теперь объединяем оба полученных множества: 
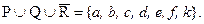И, наконец, находим дополнение к последнему множеству. Окончательно 
.
b) Сначала находим разность P \ R = { a; b; c, d }. Очевидно, что P \ R = P. Далее найдём разность этого множества с Q: P \ R \ Q = P \ Q = { a, d }. Дополнение к этому множеству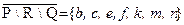 
. Находим теперь пересечение этого множества с R. Окончательно: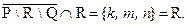 
c) Находим дополнения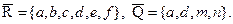 
Их симметрическая разность 
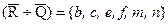. Дополнение к Р: 
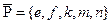. Теперь можем найти симметрическую разность 
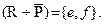Окончательно получаем: 
d) Найдём P Ç Q = { b, c }. Дополнение к этому пересечению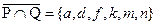 
. Пересечение Q Ç R = { k }. Дополнение 
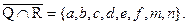Разность между найденными дополнениями 
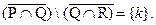Дополнение к этому множеству было найдено на предыдущем шаге. Поэтому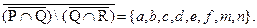 
e) Очевидно, что пересечение V с R будет не что иное, как R, то есть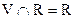 
. Отсюда получаем, что 
. Далее найдём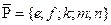 
и симметрическую разность 
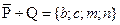. Окончательно получаем: 
.
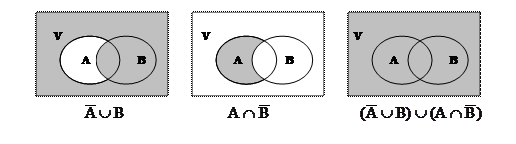
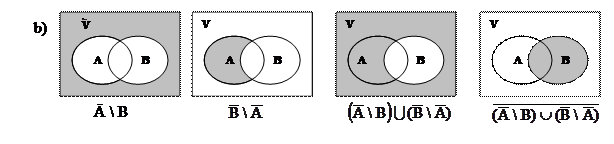
Задача 3.3. Для двух произвольных множеств А и В построить диаграммы и найти следующие множества:
a)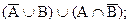 
b)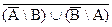 
;
c)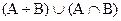 
Решение.
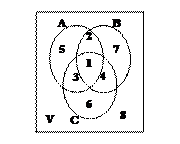
Задача 3.4. Даны три произвольные множества А, В и С. Построить диаграммы и описать следующие восемь множеств, на которые разделится универсальное множество.
Решение.
- Область 1 – это пересечение трёх множеств А, В и С. Значит эта область может быть описана выражением А Ç В Ç С;
- Область 2 получится, если из пересечения А с В убрать элементы множества С, тоесть
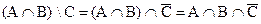; - Область 3 аналогична обл. 2:
; - Область 4:
; - Область 5 проще всего получить пересечением множества А с множествами
, то есть 
; - Область 6:
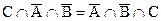; - Область 7:
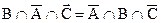; - Область 8 – это дополнение к объединению трёх множеств:
.
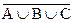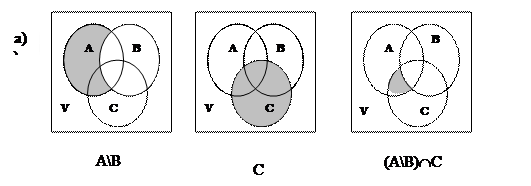
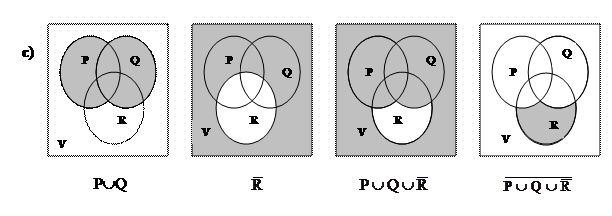
Задача 3.5. Для трёх произвольных множеств А, В и С построить диаграммы и найти следующие множества:
a) (A\B)ÇC;
b) A\(B¸C);
c)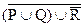 
.
Решение.
Задачи для самостоятельного решения.
1. Записать универсальное множество и выполнить над множествами А = { о, т, с, ф, х }, В = { т, с, у, х }, C = { x, y }, D = { о, к, е, ф } следующие операции:
a) (A¸B)\(CÇD);
b) (A\B)\(C\D);
c)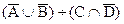 
;
d) 
.
2. Построить диаграммы для трёх произвольных множеств А, В, С:
a) (AÈB)Ç(AÈC);
b) (A¸B)È(AÇB);
c)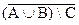 
;
d)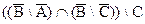 
;
e) 
.
сновные законы алгебры множеств
Рассмотренные операции над множествами подчинены некоторым законам, которые напоминают известные элементарные законы алгебры чисел. Этим определяется название алгебра множеств, которую часто называют булевой алгеброй множеств (по имени английского математика Джона Буля). Эти законы выражаются тождествами, справедливыми независимо от конкретного смысла входящих в них множеств, которые являются подмножествами некоторого универсального множества.
1. Закон идемпотичности: А È А = А; А Ç А = А,
2. Закон тождества: А È Ø = А; А È V = V; А Ç Ø = Ø; А Ç V = А,
3. Закон дополнения: A È Ā = V; А Ç Ā = Ø;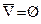 
; 
,
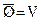4. Закон коммутативности: А È В = В È А; А Ç В = В Ç А,
5. Закон ассоциативности: А È (В È С) = (А È В) È С; А Ç (В Ç С) = (А Ç В) Ç С,
6. Закон дистрибутивности: А È (В Ç С) = (А È В) Ç (А È С); А Ç (В È С) = (А Ç В) È (А Ç С),
7. Законы де Моргана: 
,
8. Закон поглощения: (А È В) Ç А = А; (А Ç В) È А = А,
9. Закон исключения (склеивания): (А È В) Ç (Ā È В) = А; (А Ç В) È (Ā Ç В) = А,
10. Закон инволюции: 
.
Законы алгебры множеств по отношению к операциям пересечения (Ç) и объединения (È) подчинены принципу двойственности: если в каком-либо законе все знаки пересечения заменить знаками объединения, а все знаки объединеия – знаками пересечения, знак универсума (V) заменить знаком пустого множества (Ø), а знак пустого – знаком универсума, то получим другой закон.
При записи условий различных примеров часто используются обозначения:
Þ - если…, то…;
Û - тогда и только тогда, когда….
Задача 4.1. Упростить выражения алгебры множеств:
a)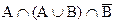 
;
b) 
;
c)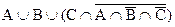 
.
Решение.
a) 
, так как на основании закона поглощения имеем, что 
;
b) так как RÈV = V, PÈÆ= P, то
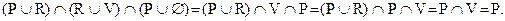
c) применим закон де Моргана для выражения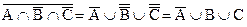 
, тогда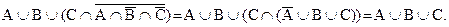 
Задача 4.2. Доказать тождества:
a) (АÈВ)\В = А\В;
b) АÇ(ВÈС) = А\(А\В)Ç(А\С).
Решение.
a)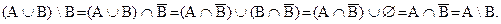 
b)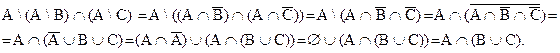 
Задача 4.3. Доказать следующие соотношения двумя способами: с помощью диаграмм и с помощью определения равенства множеств.
a)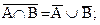 
b) AÇ(BÈC) = (AÇB)È(AÇC);
c)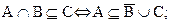 
d)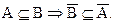 
Решение.
a)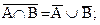
1. Доказательство с помощью диаграммы:
|
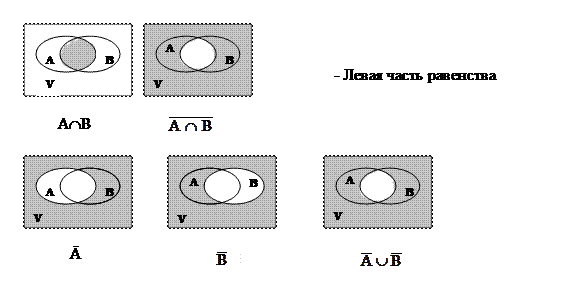
2. Доказательство с помощью определения равенства множеств.
По определению, множества Х и Y равны, если одновременно выполнены соотношения: XÍY и YÍX.
Сначала покажем, что 
Пусть х – произвольный элемент множества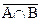 
, то есть х Î 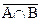. Это означает, что х ÎV и х Ï 
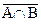. Отсюда вытекает, что х ÏА или х ÏВ. Если х ÏА, то тогда х ÎĀ, а значит, 
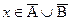. Если же х ÏВ, то 
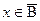, а значит, 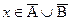. Таким образом, всякий элемент множества 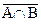есть также элементом множества 
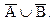То есть
Теперь докажем обратное, то есть, что 
. Пусть 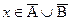. Если х ÎĀ, то х ÎV и х ÏА, а значит, х ÏАÇВ. Отсюда следует, что 
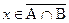. Если же 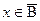, то х ÎV и х ÏВ. Значит, х ÏАÇВ, то есть 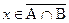. Отсюда следует, что всякий элемент множества 
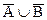является также элементом множества 
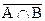, то есть .
Значит,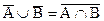 
, что и требовалось доказать.
b) AÇ(BÈC) = (AÇB)È(AÇC);
1. Доказательство с помощью диаграммы:
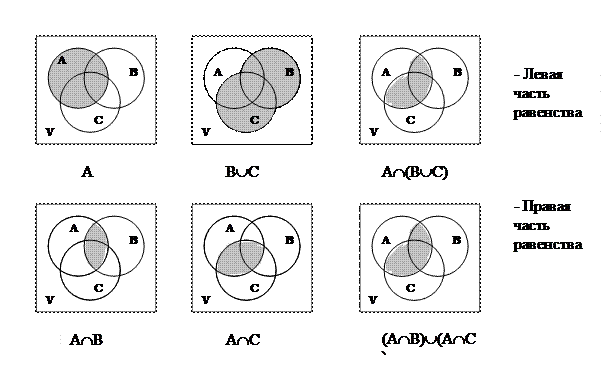
2. Доказательство с помощью определения равенства множеств.
Пусть х ÎАÇ(ВÈС). Тогда х ÎА и х ÎВÈС. Если х ÎВ, то х ÎАÇВ, что не противоречит, а значит, х Î(АÇВ)È(АÇС). Если же х ÎС, то х ÎАÇС. Следовательно, х Î(AÇB)È(AÇC). Итак, доказано, что AÇ(BÈC) Í (AÇB)È(AÇC.
Пусть теперь х Î (AÇB)È(AÇC). Если х ÎАÇВ, то х ÎА и х ÎВ. Отсюда следует, что х ÎА и х ÎВÈС, то есть х ÎАÇ(ВÈС). Если же х ÎАÇС, то х ÎА и х ÎС. Отсбда вытекает, что х ÎА и х ÎВÈС, то есть х ÎАÇ(ВÈС). Таким образом (AÇB)È(AÇC)Í AÇ(BÈC). следовательно, AÇ(BÈC) = (AÇB)È(AÇC). Что и требовалось доказать.c) 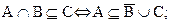Пересечение множеств А с В есть подмножеством множества С тогда и только тогда, когда множество А является подмножеством объединения множеств не-В и С.
1. Доказательство с помощью диаграммы:
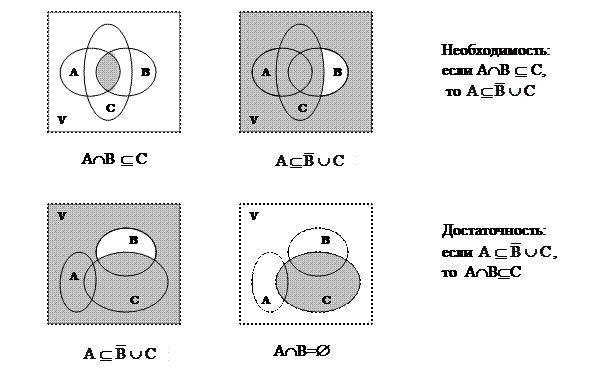
При доказательстве достаточности мы получили, что АÇВ=Æ. Очевидно, что ÆÌС, поэтому соотношение доказано. При доказательстве был рассмотрен самый общий случай. Однако здесь возможны ещё некоторые варианты при построении диаграмм. Например, случай равенства АÇВ=С либо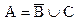 
, случай пустых множества и так далее. Очевидно, что все возможные варианты учесть бывает затруднительно. Поэтому считается, что доказательство соотношений с помощью диаграмм не всегда является корректным.
2. Доказательство с помощью определения равенства множеств.
Необходимость. Пусть АÇВÍС и элемент х ÎА. Покажем, что в этом случае элемент множества А будет являться также и элементом множества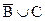 
.
Рассмотрим два случая: х ÎВ или .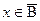
Если х ÎВ, то х ÎАÇВÍС, то есть х ÎС, и, как следствие этого, 
.
Если же 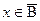, то и . Необходимость доказана.
Пусть теперь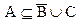 
и х ÎАÇВ. Покажем, что элемент х также будет элементом множества С.
Если х ÎАÇВ, тогда х ÎА и х ÎВ. Поскольку 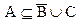, значит х ÎС. Достаточность доказана.
d) 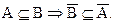Если множество А является подмножеством множества В, то тогда множество 
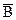будет подмножеством множества Ā.
1. Доказательство с помощью диаграммы:
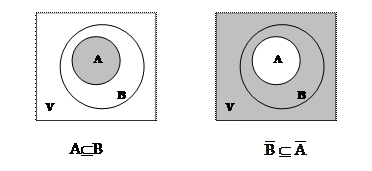
2. Доказательство с помощью определения равенства множеств.
Пусть АÍВ. Рассмотрим элемент х ÏВ (или 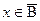). Аналогично: х ÏА (или х ÎĀ). То есть всякий элемент множества 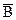есть также элементом множества Ā. А это может быть в случае, если 
. Что и требовалось доказать.
Задача 4.4. Выразить символически указанные области и упростить полученные выражения.
Решение.
а) Искомая область состоит из двух изолированных частей. Условно назовём их верхней и нижней. Множество, которое они изображают, можно описать так:
М = { x ô x ÎA и х ÎВ и х ÏС или х ÎС и х ÏА и х ÏВ}.
Из определения операций над множествами получим: М = ((АÇВ)\С)È(С\А\В). Запишем это выражение с помощью основных операций – дополнения, объединения и пересечения: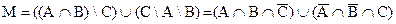 
. Упростить это выражения нельзя, поскольку имеем по одному вхождению каждого символа. Это и есть простейший вид данной формулы.
c) Данную область можно рассматривать как объединение множеств А\В\С и АÇВÇС. По определению M = { x ô x ÎA и x ÏВ и х ÏС или х ÎА и х ÎВ и х ÎС}. Упростим:
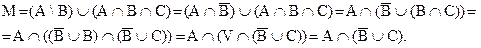
Задачи для самостоятельного решения.
1. Упростить:
a)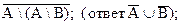 
b) (А¸В)È(АÇВ); (ответ АÈВ);
c)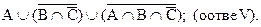 
2. Доказать с помощью диаграмм, законов алгебры множеств и определения равенства множеств:
a) (АÈВ)\В = А\В;
b) АÇ(ВÈС) = А\(А\В)Ç(А\С);
c) АÈВ = АÇВ Þ А=В;
d) А\В = Æ Û АÇВ = А.
3. Выяснить, существует ли множество Х, удовлетворяющее при любом А равенству:
a) АÈХ = А; (ответ Æ);
b) АÇХ = А; (ответ V).
