ДП-метод нахождения оптимального реш-я в задачах с многошаг-й струк-рой.
Ососбенности зад-ч ДП:
1.Рассматривается сис-ма, состояние которой на каждом шаге определяется вектором состояния xt. Дальнейшие изменения её состояния зависят только от данного состояния xt и не зависят от того, каким путём сис-ма принесла в него.Такие процессы называются процессами без последствий.
2.На каждом шаге выбирается одно решение(управление) Ut,под действием которого сис-ма переходит из предыдущего состояния xt-1 в состояние xt. Это новое состояние является функцией состояния на начало шага и принятого в начале шага решения xt= xt (xt-1, Ut).
3.Действие на каждом шаге связаны с опред-м выигрышем или потерей,котор.зависят от состояния на начало шага и принятого реш-я.
4.На векторы состояния и управ-я могут быть наложены ограничения,объединение которых образует область допустимых решений Ω.
5.Требуется найти такое допустимое управление Ut для каждого шага t,чтобы получить экстремальное значение ЦФ за все T-шагов.
Любую допустимую последовательность действий для каждого шага,переводящее сис-му из начальн.шага в конечн.называют стратегией управления(СУ). Допустимую СУ,которая доставляет ЦФ экстремальное значение назыв-ся оптимальной.
онятие о ДП.Геометрич-я интерпретация задач ДП.
ДП( динамическое планирование )- метод нахожд-я реш-я в з-чах с многошаговой стр-рой.
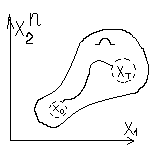
Геом-я интерпретация задач. Пусть N -размерность простр-ва состояния.В любой момент времени корд-ты сис-мы имеет вполне опред-ное знач-е,кот. с изм-нием времени мож. изм-ся.Переход сис-мы из одного сост-ния в др наз-ся траекторией его движения в простр-ве сост-ний.Прост-во,в кот. корд-ми служат сост-ние сис-мы наз-ся фазовым. Рассм-м двумерное простр-во сост-ний(рис):обл. доп-мых реш-й изобр-на фигурой Ω, х0 -начальное сост-ние сис-мы, хТ -конечное.
Для многих эк-ких задач неизв-ны началь-е или конеч-е сост-ние,а изв-ны обл-ти,кот-м принадл-ат данные сост-ния.Задача ДП сост-т в том,чтобы найти фазовую траекторию, кот. нач-ся в обл-ти х0 и заканч-ся в обл. хТ ,для кот. знач-е ЦФ достигало бы экстр-го знач-я.Если известны нач-ное и конеч-е сост-ния, то такие задачи наз-ся з-чами с закрепл-ми концами. А если изв-ны нач-ные и конеч-е обл-ти,то такие задачи наз-ся з-чами со свободными концами.
ринципы ДП(пр-пы ДП).
Суть метода ДП -идея постепенной,пошаговой оптимизации.Если трудно решить слож-ю задачу,то её след-т разбить на ряд более простых.Каждая новая задача оптим-ся не отдельно от осталь-х,а упр-ние на каждом шаге выбир-ся с учетом всех его последствий. Исключ-е -послед-й шаг,кот. мож. план-ся без учета посдед-вий. Особ-сть ДП:всю ДП целесообр-но разворач-ть от конца к началу.В перв. очередь план-ся N-й шаг,за ним (N-1).Для (N-1)-шага возмож-ми исходами будут явл-ся хN-1.Набор опти-х упр-ний,зависящих от возм-ных исходов предыд-го этапа наз-ся условным оптим-ым реш-ем U*N (хN-1).Для предпос-го этапа:требуем,чтобы ЦФ достигала экстр-го знач-я на 2-х послед-х этапах вместе,что позволит найти условно оптим-ное реш-е на предпосл-ем U*N-1 (хN-1)…и для первого этапа U*1 (х0).Т.к. х0 задано однозначно,то найдем оптим-ое упр-ние для 1-го шага и экстр-ное знач-е ЦФ относит-но всего процесса,аналогично для 2-го шага U*2 (х*1) и т.д.Таким обр. задачи ДП реш-ся дважды:
1)от конца к началу(в рез-те нах-ся оптим-ое упр-ние и условно оптим-ое знач-е ЦФ для каждого шага,оптим-ое реш-е для 1-го шага и оптим-ое знач-е ЦФдля всего процесса);
2)от начала к концу(нах-ся оптим-ое упр-ние на каждом шаге с точки зрения всего процесса).
2 основных принципа ДП:
1) пр-п оптимальности: оптим-ое упр-ние на каждом шаге опред-ся сост-ем сис-мы на начало шага и целеупр-нием.Этот пр-п выраж-ся в состоянии рекуррентных соотнош-й Беллмага.
2) пр-п погружения: на каждом шаге реш-ся задачи наимень-го размера,но с такой же целью как и общая задача.
43). Функц-е ур-ния БЕЛЛМАНА.Будем сч-ть,ч.нач-е Х0и кон-еХтсостояния сист.заданы.Об-чим ч/зf1(x0,u1)-зн-ние ф-ции цели на1-м этапе,при нач-м сост-и сист.x0 и при упр-нии u1,ч/з f2(x1,u2)-зн-ние ф-ции цели на2-м этапе ит.д….и fn(xn-1,un) зн-ние ф-ции цели на n-м этапе,тогда F=f(x0,u)= 
(1).Треб-ся найти оптим.ур-ниеU*=U1*,U2*,…,Un*)такое,ч.достав-етЦФ1экср-е зн-е,при огр-яхU€Ω,гдеΩ-обл.опр-я исх.з-чи.Введем обоз-нияΩN,ΩN-1,N,ΩN-2,N,… Ω1,N,=Ω-обл-ти опр-ния дан.з-ч на посл-м этапе,2-х посл-х этапах ит.д. F1(xN-1), F2(xN-2),… FN(x0)-зн-яЦФна посл-м этапе,2-х посл.ит.д.
Пусть сост-е xN-1з-ны,тогда F1(xN-1)=max(min)поUn€ΩfN(XN-1,UN) (2); F2(xN-2)=max(min)поUn€ΩN-1,N(fN-2(XN-2,UN-1)+ F1(xN-1)) (3); FN(x0)=max(min)поU1€Ω1,N(f1(x0,u1)+ FN-1(x1)) (4).Ф-лы2-4наз-ся функц-м ур-нием Бел-на.для того,ч.найти оптим ур-ние наNшагах,нужно знать усл.-оптим.ур-ния на предшес-х N-1шаге.
44) З-ча оптим-го маршрута.Треб-ся найти мар-т,связ-й городаАиВ,для кот.сум-е з-ты на перев-ку груза были бы наим-ми.Разобьем все мн-во гор-в на подмн-ва.В1-е п/мн-во вкл.в-ну1(А),во2-е вкл.в-ны,в кот.вх-т дуги из1-го п/мн-ва ит.д.Перенум-м этапы от конечной в-ны n нач-ой и введемобозн-я:n-номер шага,сij-ст-ть перев-ки груза из г-даiв г-дj,fn(i)-ст-ть перев-ки груза(minз-ты) на перев-ку груза г-да i до кон-го г-да,если до кон0го г-да ост-сь n шагов,jn(i)-№г-да,ч/з кот.надо ехать из г-да i,ч.достичь fn(i).n=0cлед,ч.мы нах-ся в кон-м г.(В),зн-т fn(i)= f0(В)=0;n=1след-но пред-м,ч.мы нахся или в г.i1или в г.i2..Для этих г-дов з-ты на пер-ку сот-ят f1(i1)=ci1,B+f0B, f1(i2)=ci2,B+f0B,в рез-те найдем i,j1(i)ч/з какой г-д ехать;n=2след.пред-м,ч.кон-й г-д груз мож.быть доставлен или из г-даS1,S2,S3. f2(S1)=minпоj(Cs1,i1+f1(i1), Cs1,i2+f1(i2)), f2(S2)=minпоj(Cs2,i1+f1(i1), Cs2,i2+f1(i2)), f2(S3)=minпоj(Cs3,i1+f1(i1), Cs3,i2+f1(i2))РИСУНОК..мы найдем из к-го и ч/з какой г-д,т.е.i,j2(i)
Ур-ниеБел-на для этой з-чи fn(i)=minпоi,j(Cij+fn-1(j)).
45). З-ча оптим-го распр-я ср-в.n-предпр-ем выдел-ся ср-ва с.В зав-ти от выдел.суммы 0≤х≤с по каж-му пр-тию известен возм.прирост выпуска прод-и был max.
n=1-ден.ср-ва выд-ся 1-му пр-тию.Каж-му знач-ю Х по усл-ю з-чи соотв.опред-ое единств.знач-е q1(х),зн-т мож.записать,что общ.прирост f1(х)=q1(х),0≤х≤с.
n=2-ден.ср-ва с распред-ся м/ду 2-мя пр-ями.Если2-му пр-тию буд.выд-на сумма Х,то прирост прод. На нем составит q2(х).зн-т 1-му пр-тию остан-ся(с-х)ден.ед.,ч.поз-итувел-ть выпуск прод.до приростаf1(с-х).Зн-т общ прирост составит q2(х)+ f1(с-х).Опт-му зн-ниюf2(с) буд-т соот-ть так.зн-ние Х,для кот.посл-я сумм.буд.макс-й f2(с)=max(q2(х)+ f1(с-х)), 0≤х≤с.Для всех n-пр-тий fn(c)=max(qn(х)+ fn-1(с-х)), 0≤х≤с.max прирост вып.прод.на n пр-тиях опр-ся как maxсум.прироста на n-м пр-тии и прироста вып.отдел.n-1-м пр-тии при усл-и,что ост-ся после n-го пр-тия ср-ва м/дуо стал-ми пр-ями распр-ся оптим-но.
46)З-ча план-ния пр-венной прогр-мы.Рассм.пром-к,сост-й из Т мес-в,запас прод. на складе на нач.пл.пер.=i0ед,спрос на прод в каж-м из месс-в=Dt,t=1.РИСУНОК.Опр-ть пр-вен.пр-му изгот-я прод.,удовл-ю спрос в к-м из мес-в пл.пер.и обеспеч.minз-ты на пр-во и хран-е прод.Запас прод на складе в конце пл.пер.дол.б.=0.Общ.з-ты на пр-во и хр-ние прод.Сt(xt,it)сост-т из з-т на пр-во Сt(xt)и з-т на хр-ниеед.прод.h•it,гдеh-з-ты на хр-ние,it-запасы на кон.мес.З-ты на пр-во=усл.пропорц.+пропорц.з-ты Сt(xt,it)=k+l• xt+h• it.Склад-е пло-ди огр-ны в-нойМ,а пр-вен.мощ-ти-в-нойВ.Введем след.обозн-я:n-№шага,соотв.обратной нумерации мес-в,dn спрос на прод.на n-м отр.,in-запас прод.на нач. n- го отр.,xn(in) кол-во пр-ва прод. на n-м отр.,если запас прод.на нач.этого отр.сост-т inед., jn –запас прд.на кон.n-го отр.,Cn(xn,jn) з-ты,связ.с выпуском хnед.прод.,с сод-ем зап-в,Vкот.на кон. n- го отр.=jnед., fn(in)-зн-еЦФ=з-там на пр-во и хр-ние прод.за n посл.мес-в,если ур-нь зап-в на нач.n-го месс.=inед,где n=1,N=T
n=0т.к.запас прод.на к.план.пер.д.б.=0 
f0(0)=0
n=1.Запас прод.на нач.этого отр-ка i1неизв-н,но он м.б.=люб.цел.неотриц.числу,не превыш.вместимости скдладаМи спроса в расс-ом отр.d1=>i1=0,1,…,min(d1,M).Для удовл-ния спроса на прод.Vпрод.д.б.=x1=d1-i1=>f1(i1)=c1(x1,j1)=c1(d1-i1,0)
n=2. Запас прод.на нач.2-го отр-ка=i2.Зн-яi2м.прин-тьлюб.неотр.целоч-е зн-я,непревыш.min(d1+d2,M).кол-во пр-ва прод.на 2отр.х2в азв-ти от за-ний i2д.б.не<d1-i2,т.к.спрос на 2-м отр.д.б.уд-н,но не >чем min(d1+d2-i2,B).Мин.з-ты на пр-во и хр-ние прод.за 2 посл.мес.составят f2(i2)=minпоx2(c2(х2,j2)+f1(i1)),гдеi2==0,1,…,min(d1+d2,M).,d2-i2 
x2 min(d1+d2-i2,B). Общ.реккурентное соотнош-е им.вид: fn(in)=minпоxn(cn(хn,in+xn-dn)+fn-1(in+xn-dn)),гдеin==0,1,…,min(d1+d2+…dn,M).,dn-in xn min(d1+d2+…+dn-in,B).Далее необх.пр-ти выч-я по ф-ле:fN-1(iN-1),iN-1=0,1,…,min(d1+d2+…dN-1,M).fN(i0),i0-зад-н.зн-я.На основ-и получ-х расч-в м.найти объемы вып.прод.в к-м мес.соотв.оптим.пл.реш-я з-чи.
48)Геометр.интерп-ция з-чиНП.Общ.з-чей НП наз-ся з-ча вида
max(min)F=f (x1, x2,…, xn) (1)
φi (x1, x2,…, xn) 
(2),в кот.либо ЦФ 1,либо огр-ния,либо те и др.нелин-е.В рез-те реш-я эт.з-чи буд.найдена т.Х* такая,что для любой др.т-ки Х,коор-ты кот.также удовл-ют огран-ям з-чи и выпол-ся не=во
f(x*)> f(x)(если з-ча на min,то f(x*)< f(x)).В отлич.от з-чиЛП ОДР НПне всегда явл.выпуклой.Т.,в кот.достиг-ся экстр-м ф-ции мож.нах-ся как на границеОДР,так и внутри нее. Алгоритм граф.м-да: строимОДРз-чи,если она пуста,то з-ча не имеет реш-я,2)строим гиперпл-ть f(x1, x2,…, xn)=h,3)опред-им гиперпл-ть наив.(наим.)ур-ня или опр-им неразд-ть з-чи из-за неогр-тиЦФ,4)нах-м т-куОДР,в кот.ЦФ достигает экстр-го знач-я и нах-м в ней знач-е ЦФ.
49)Метод множ-лей Ланг-жа реш-я задачНП.Экон-й смысл множ-ей Ланг-жа
Рассм-м частный случай общ.з-чи
max(min)F=f (x1, x2,…, xn)
φi (x1, x2,…, xn)=bi, i=1,m
для того,ч.найти ее реш-е сост-ем ф-цию Ланг-жа,безусловный экстр-м кот.совпад. с условным экстр-ом
L(x1, x2,…, xn,λ1, λ2,…, λn)= f (x1, x2,…, xn)+ 
(bi- φi (x1, x2,…, xn))
Для эт.ф-ции запи-ем необх-е усл-е экстр-ма 
Решив посл-юю сист.,мы найдем все критич.точки,в кот.ф-ция может иметь экстремум знач-я.Затем с пом.достат.усл-й определяем точки экстремума ф-ции.
Алгоритм: 1)сост-ем ф-цию Ланг-жа,2)нах-им част-е произв-е ф-ции Л-жа по всем перем-м и при=ваем их к0,3)реш-в сист.ур-ний,найдем стационар-е точки,т.е.точки,в кот.ЦФ мож.иметь экстр-м,4)среди стацион-х точек с примен-ем достат.усл-й нах-им те,в кот.ф-ция имеет экстср-мы
Экон.сод-ние множ-лей Л-жа λi:рассм-м прост-шую з-чу оптим-ции
max(min)F=f (x1, x2)
φi (x1, x2)=b.Предпол-м,что экстр-м достиг-ся в как.-то точке Х*=(x1*, x2*), F*=f(x1*, x2*).пусть координаты x1*и x2*,а значит и F*от знач-й прав.части b
x1*=x1*(b), x2*=x2*(b), F*=f(x1*(b), x2*(b)).Найдем част.произв-еЦФ по x1 и x2 в завис-ти от b
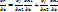(1)из осн-х огран-й след-т,что част.произв-я ф-ции φ
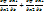=1(2)в экстр-й точке вып-ся необх.усл-е экстр-ма 
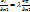и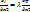 
(3).Подставим в 1-ую 3,испол-я2 
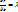.для з-ч,у кот.кол-во огран-й=m,т.будет спрвед-ва ф-ла 
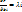,i=1,m
50) Градиент.метод решения задачНП
Используя град.метод,можно найти решение люб.з-чиНП,но дан.методы целесообразно испол-ть для нахожд-я решения з-ч выпуклого прогр-ния,т.е.,когда локал.экстремум явл.одновр-но и глобал-м.Для примера будем рассм-ть з-чу макс-ции диффер-й функции.
Решение нач-ся с определен.точкиХ0,корд-ты кот.удовл-ютОДР.В эт.точке находим градиент ф-ции 
.Сделав небол шаг в найд-м напр-ии,перех-м какую-то т.Х1,в кот.опять ищем оптим.напр-ие gradF(X1)и т.д.
Проц.нахож-ия реш-я пред.соб.ломаную линию Х0,Х1,Х2...в точ-х эт.ломаной знач-яЦФдолжны сход-ся F(x0)< F(x1)< … <F(x*).Переход от т.Хк к т.Хк+1 осущ-ся по прямой,ур-ние кот. Опр-ся из ур-ния Хк+1=Хк+λк• gradF(Xк),где λ к –шаг,знач-е кот.опред-ся по фор-ле: gradF(Xк+1)• gradF(Xк)=0.
Если окаж-ся,что F(xк+1)< F(xк),то следует вернуться в т. Хк и умен-ть шаг λ к. Итерацион-й проц.осущ-ся до того момента,пока град-т ф-ции в очередной точке не станет=0 или пока не выпол-ся не=во I F(xк+1)- F(xк)I≤ξ,гдеξ-очень мален-е полож-е число.
