Рассмотрим пару симметричных двойственных задач
max F=∑cjxj
∑aijxj≤bi,i=1,m; j=1,n (1)
xj≥0,j=1,n
min α=∑biyi, i=1,m
∑aijyj≥cj, j=1,n;i=1,m (2)
yi≥0, i=1,m
Теорема. Для любых допустимых планов Х=(х1,х2,…,хm) и Y=(y1,y2,…,ym) прямой и дв-ной задач ЛП справедливо неравенство
F(X)≤α(Y), т.е.
∑cjxj(j=1,n)≤∑biyi(i=1,m) (3)
Доказательство:
F(X)=∑cjxj(j=1,n)≤∑(j=1,m)(∑aijyi(i=1,n))xj=∑(i=1,m)yi∑(j=1,n)aijxj≤∑(i=1,m)biyi=α(Y)
Эк-ое содержание теоремы: для любого допустимого плана производства Х и любого допустимого вектора оценок ресурсов У общая созданная стоимость не превосходит суммарной оценки ресурсов.
22)Критерий оптимальности Канторовича
Теорема. Если для некоторых допустимых планов Х* и У* пары дв-ных задач выполняется равенство F(X*)=α(Y*),то Х* и У*- оптимальные планы соответственно.
Доказательство: согласно осн-му неравенству теорем дв-ти для любого допустимого плана Х прямой задачи и любого допустимого плана У* дв-ной задачи выполняется неравенство F(X)≤α(Y*),но по условию теоремы F(X*)=α(Y*).В силу транзитивности отношений «≤» и (=) имеем F(X)≤F(X*),но т.к. Х-произвольный допустимый план, то тогда F(X*)=maxF.Значит, Х*-оптим. план прямой задачи. Аналогично доказывается, что У* явл-ся оптимальным для дв-ной задачи.
Эк. содержание: план производства Х* и вектор оценок ресурсов У* явл-ся оптимальными тогда, когда цена всей произведенной продукции и суммарная оценка ресурсов совпадает.
алая теорема дв-ти.
Для существования оптимального плана любой из пары дв-ных задач необх-мо и достаточно существование допустимого плана для каждой из них.
Доказательство: пусть задачи дв-ной пары имеют оптим-ые планы Х* и У*. Это значит, что F(X*)=maxF, a α(Y*)=minα, т.е. Х* и У* принадлежат области допустимых решений, следовательно, соответствующие системы ограничений пары дв-ных задач совместны. Они имеют хотя бы по одному допустимому плану Х* и У*.
Достаточность: пусть каждая из дв-ных задач имеет допустимый план. Докажем, что эти задачи имеют оптим-ые планы. Пусть У*- допустимый план дв-ной задачи. Согласно осн-му неравенству теории дв-ти для любого допустимого плана Х прямой задачи имеет место неравенство F(X)≤α(Y*). Решая прямую задачу симплексным методом, получаем последовательность опорных решений х0,х1,х2,…, для кот-х значение ЦФ будет равно F(x0), F(x1), F(x2),…В силу последнего неравенства эта последовательность сходится, т.е. ограничена сверху. Значит найдется наибольшее значение ЦФ F(X)≤F(X*), а Х* принадлежит обл-ти допустимых решений=>значит явл-ся допустимым.
24)Первая теорема двойственности и ее экономическое содержание. Теорема: Если 1 из пары двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные значения ЦФ равны: F (X)=φ(Y). Если одна из пары дв-х задач неразрешима вследствие неограниченности ЦФ на множ. доп-х решений, то система ограничений другой задачи противоречива.
махF =c1x1+c2x2+…+cnxn
a11x1+a12 x2+…+a1nxn ≤ b1 + xn+1
….....
am1x1+am2x2+…amnxn≤ bm +xn+m
xj≥0, j=1,n
minφ= b1y1+ b2y2+…+ bmym
a11y1+a21 y2+…+am1ym ≥c1 - ym+1
….....
a1ny1+a2ny2+…amnyn≥cm - yn+m
yi≥0, i=1,m
Соответствие м. перем.дв-х задач: x1 x2 …xn - ym+1, ym+2,…, ym+n-СП, xn+1, xn+2,…, xn+M - y1, y2,…,ym – БП. Решение двойственной задачи нах. в посл. симпл. табл, содер. оптим. план прямой задачи. Экономическое содержание: если разреш задача опред-ия оптим-го плана максим-го выпуск прод-ии, то разр-ма и задача опр-ия оценок ресурсов. Причем цена пр-ва прод-ии и сумм-ая оценка сов-т.
25) теорема о недоп-ей нежесткости и ее экономич-ое сод-ие. Теорема: для того, чтобы планы Х*, У* пары двойст-х задач были оптим-ми необх и достат вып-ие след-х усл-ий: хj*(∑аijyi*- сj)=0, j=1,n (1), yi*(∑аijxi*- bi)=0, i=1,m (2). Док-во: необходимость махF =∑cjxj, ∑аijxi*= bi, i=1,m, xj≥0, j=1,n. (3) minφ= ∑biyi ∑аijyi* ≥сj, j=1,n yi≥0, i=1,m. F (X*)=φ(Y*) т.е∑cjxj,* = ∑biyi * (4). Подставим в 4 bi из 3: ∑cjxj,* =(∑аijxi*) yi*= ∑хj*∑аijyi*→ ∑хj*(∑аijyi*- сj)=0 (5). Т.к хj*≥0, и ∑аijyi*- сj ≥0, j=1,n. След-но из рав-ва 5 след-т условие 1, усл 2 док-ся аналогично. Достаточность: ∑ хj*(∑аijyi*- сj)= ∑ хj*∑аijyi*-∑cjxj,*= ∑yi*∑аijxi* - ∑cjxj,*= ∑biyi * - ∑cjxj,*→ F (X*)=φ(Y*). Экономическое содержание: Двойственные оценки могут служить мерой дефицитности ресурсов (ДР).ДР, т.е ресурс по опт-му плану пр-ва исп-ся полностью имеет полож-ю оценку, а избыт-й имеет нулевую оценку.
27) Постан-ка ТЗ по критерию ст-ти. m – поставщики, кол-во груза а1, а2,…,аm. n – потребители, потребность в грузе b1, b2,…,bn. Cij, j=1,n, i=1,m – тарифы перевозок. Сост-ть план перевозок груза от m к n, при кот-м сумм-ые тран-е изд-ки будут минимальными. Ограничения по запасам ∑хij= аi,i=1,m. ∑хij= bj, j=1,n. Все хij ≥0 этим исключены обр-ые перевозки. Общ-е затраты на перевозку сост-т minF= c11x11+ c12x12+…+ c1nx1n+ c21x21+ c22x22+…+ c2nx2n+…+ cm1xm1+ cm2xm2+…+ cmnxmn=∑∑cijxij.
| n m | b1 | b2 | … | bn |
| а1 | c11 x11 | c12 x12 | …. | c1n x1n |
| а2 | c2n x21 | c21 x22 | …. | c2n x2n |
| … | … | …. | …. | … |
| аm | cm1 xm1 | cm2 xm2 | …. | cmn xmn |
28) теорема о сущ-ии допустимого плана. Необх-мо и дост-но вып-ие равенства ∑аi=∑ bj (1) Док-во: необходимость ∑хij= аi,i=1,m ∑хij= bj, j=1,n. Очевидно, что элементы хij сумм-ся какпо стр-м, так и по ст-ам, различие лишь в перестановке этих элементов, от перестановки мест слог-х сумма не меняется: ∑аi=∑ bj. Достаточность: если вып-ся условие 1, то всегда имеется доп-ый план ∑аi=∑ bj=А. элементы хij выразим ч-з данные задачи: хij=аibj/А i=1,m j=1,n (2). Следов-но все хij ≥0 i=1,m j=1,n этот набор неотр-х чисел будет сост-ть доп-ый план тогда когда он будет удовл-ть системе осн-х огранич. Просуммируем 2 по всем j →∑хij= 
∑ bj= аi i=1,m. Анологично просуммируем 2 по i→∑хij= 
∑ ai= bj 
=1,n. Мы показали, что набор чисел 2 удовл. системе ограничений задачи, след-но он явл доп-ым планом.
29) Закр. и откр.модель ТЗ. Теор. о ранге матрицы.
Мод.ТЗ наз.закрытой, если суммарный объём груза, имеющ. у поставщиков, равен сумм-ному спросу, т.е. выполн. рав-во: 
= 
В случае закрыт. мод. весь имеющ-ся груз полностью развозится поставщ-ми и все потребн-ти потребит. полностью удовлетв. Мод. ТЗ наз. открытой, если выполн. одно из усл-й:а) > , б) < . В случ. а) Все потребит. Будут удовлетв., но при этом у некот. пост-в ост-ся излишки груза. В случ. б) весь груз пост-ми будет вывезен, но потр-ти потребит. будут полностью неудовлетв. Для разреш-я з-чи с откр. м-ю, её необх. преобр-ть в закр-ю. В сл. а) ввод-ся фиктивный (n+1)-й потребитель, кот. будет = bn+1=∑ai-∑bj. В этом сл. в трансп. табл. добав-ся еще 1 столбец. В сл. б)введ-ся фиктивный (n+1)-й поставщик, запас груза, у кот. = am+1==∑bj-∑ai. Тарифы у фиктивн. потребит. (поставщ.)=0.
Теор. о ранге матрицы. ТЗ явл. Задачей ЛП и ее можно реш. симплексн. мет. Однако специфич. Особенности сист. осн. огранич-х позволили разработ. для ТЗ более простые методы реш. Эти особен-ти сост. в след-м: 1)коэф. При перемен-х во всех ур-х =1 либо 0. 2)каждая перемен. Встреч-ся в 2-х и только в 2-х уровнен. 3)сист. уравнен-й симметрична относит-но всех перемен. Xij. теоремы заключ-ся в том, что кол-во занятых ОП клеток д.б. (m=n-1), если занятых кл-к будет<, то став. число 0 и кл-ка счит-ся занятой.0 нельзя став. в кл-х, кот. образуют цикл с занятыми кл-ми.
30) Постр-е исх.ОП ТЗ правилами «северо-зап. угла» и «миним. тарифа»
а)прав. «с-з угла». Груз распредел. с загрузки левой верхней, условно назыв-й северо-зап., кл-ки первый потребит. будет полностью удовлетв-н. В дальнейшем первый столбец в табл. в расчет не приним-ся. Двигаясь вправо по 1-й строке в кл-ку (1,2) заносимчисла x12=min(a1-b1,b2) и т.д.
б) прав. «мин. эл-та». В табл. просматр-ся все тарифы и в 1-ю оч. заполн-ся кл-ка с min тарифом. В эту кл-ку запис-ся max возм. знач-е поставки, затем из рассм-х исключ-т строку, соотв-го поставщику, запасы кот. полностью израсх-ны или столбец, потребн-ти потребит-ля кот. полностью удовлетв-ны и т.д.
31) Оптим-ть ОП ТЗ: теор. о потенциалах, циклы.
План ТЗ Х* явл. Оптим-м, если ему соотв-т система из m+n чисел Ui и Vj, кот. удовл-т след. Усл-м: 1) Ui+Vj=Cij, X*ij≠0; 2) ∆ij=cij-(Ui+Vj)≥0, X*ij=0 Док-во: ТЗ можно рассматр-ть как двойств. задачу к некот. исх. задачи,реш-ой на max. Каждому i-му огранич-ю ТЗ в исх. задаче соотв-т перемен. Ui,i=1,m, а j-му огранич-ю x1j+x2j+…+xmj=bj перем. Vj, j=1,n. Тогда задача б. иметь вид: maxφ= 
+ 
, Ui+Vj≤Cij i=1,m, j=1,n Обозн. ч/з X*,Y*(Ui,Vj)-ОП двойств. исх. з-чи. На основ-ии 1-й теор. двойственности равенство: minF=maxφ. А на основании 2-й теор. двойств. выполн. усл.: 1)Ui+Vj=Cij, xij>0; 2)Ui+Vj≤Cij, xij=0, i=1,m j=1,n Из теор. след., что для ОП ТЗ необх. выполн-е усл-й: 1)кажд. занятой кл-ке в распред. табл. соотв. ∑ потенциалов, ровная тарифу этой клетки; 2)кажд. своб. кл-ке соотв-т ∑ потенц-в, не превыш-я тарифа этой кл-ке. Эк-ки оценка показ-т на сколько ден.ед. уменьш. трансп. издержки от загрузки данной кл-ки ед. груза. Для перехода от одного ОП к другому использ-я циклы. Цикл предст. замкн-ю ломаную линию, сост-ю из звеньем, кот пересек-ся под прямым углом. Цикл. включ. 1 своб. кл-ку. В цикле всегда четное число кл-к. Цикл строится для свободн. кл-ки. Если ломанная линия пересек-ся, то точки самопересечения не явл. вершинами. Для наиб перспективн. кл-ки строится замкнутый цикл с вершинами в загружен. кл-х. Вершинами этого цикла усл. приписыв. знаки: своб. кл-ке «+», следующ. «-» и т.д. из поставок в кл-х цикла с «отриц.» верш. выбир. наименьш. кол-во груза, кот перемещ-ся. по кл-м этого цикла: прибавл. в положит. верш. и вычет. в отрицат., в рез-те чего баланс цикла не наруш. Алгоритм реш. ТЗ мет. потенциалов. 1)Усл.ТЗ записать в форме распред-й табл., но снач. провер. закр. или откр. модель ТЗ. 2) по 1-му из правил строим ОП. 3)Опред-м пот-лы поставщ-в и потреб-й, для этого реш-ся сист. ур-ний Ui+Vj=Cij для занятых кл-к. 4) Опред-ем оценки своб. кл-к ∆ij>0, то получим ОП единствен-й, если хотя бы 1 из оценок ∆ij=0, то имеем бесчислен. мн-во оптим. пл-в.
32) Усложненные постановки ТЗ.
1. Нередко целесообразно min-вать ∑-ные затраты на произв-во и транспортир-ку прд-ции. С подобной задачей м. столкнуться при реш. вопросов, связан. С оптим-м размещением производств-х объектов. Здесь м. оказаться эк-чески более выгодно доставлять сырье из отдельного источника, но зато при меньшей его себест-и. В таких задачах критерием оптим-ти служит ∑ затрат на произв-во ед=цы груза и на его перевозку.
2. Часто необходимо вводимо огранич-я, согласно кот.,отдельн. поставки от определен. поставщика определ-му. потребит. д.б. исключены, из-за отсутсвия достаточного кол-ва транспорта или необх-х условий хранения груза, чрезмерной перегрузки коммуникаций и т.п. Значит, в матрице перевозок, содержащей ОП, определен. кл-ки должны остаться своб-ми. Это достиг-ся искусствен. завышением пок-лей Cij в кл-ах, перевозки через кот-е следует запретить, до значений, заведомо больших всех, с кот. придется сравнивать в процессе реш-я задачи.
3. Иногда прих-ся учитыв. Ограничения по пропускной способн-ти некот. маршрутов. Если, напр., по маршр. AkBs можно провести не более d ед. груза, то Bs-й столбец матрицы перевозок разбив-ся на 2: Bs’ и Bs’’. В 1-ом спрос приним-ся = разности между действит-м спросом bs и огранич-ем d, во 2-м – равным огранич-ю d. Тарифы Cij в обеих столбцах одинаковы и равны данным, но в 1-ом в кл-ке, соотв-ей ограич-ю, вместо истинного тарифа Cks ставится иск-нно завыш. Тариф М (кл-ка блокир-ся). Затем задача реш. обычн. способом.
4. Возможно, что некот-е поставки по опред-м маршрутам обязательны и должны войти в ОП независ. от того, выгодно это или нет в усл-х всей задачи. Тогда соотв-но уменьш. запасы груза у поставщ-в и спрос у потребит-й и решают задачу относит-но тех поставок, кот. не обязательны.
33) ТЗ с максимиз. ЦФ.
Если в задачах трансп. типа ЦФ максимиз., то:
Нач. ОП составл. правилом «максим-го эл-та»;
Оптим-м будет ОП, кот. в распред табл. сопутствует свободн. кл-ки с положит. оценками, т.е. все ∆ij≤0;
Выбор кл-ки, подлежащей заполнению при переходе от одного ОП к другому, должен произв-ся не по отрицат-й, а по положит. оценке.
34) ЦП. Задача о контейнерных перевозках.
ЦП-раздел мат-го прогр-я, изуч-й экстрем-е задачи, в кот. на искомые переменные налагаются усл-я целочисл-ти, а обл. допуст. реш. конечная. ЭММ задачи ЦП имеет вид:
max(min)F=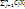 
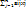{≤, =, ≥} bi, i=1,m xj≥0, и целые, j=1,n
Задача о контейн. перев. Для перевозки n видов прод-ии использ-ся контейнер с m-отсеками, прод-я характериз. св-ом неделимости. Т.е. ее можно взять в колич-ве 0,1,… Известны след. параметры: Cj, j=1,n – полезность ед. j-ой прод-ии; bi, i=1,m – вместимость i-го отсека; aij, i=1,m, j=1,n – расход i-го отсека для перевозки ед. j –й прод-ии. Треб-ся определить план перевозки X*, т.е. кол-во ед. каждого вида прод-ии, при кот. обеспечивается max-ная общая полезность рейса.
maxF= 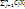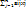≤ bi, i=1,m xj≥0, и целые, j=1,n
Если для перевозки исп-ся один отсек и каждый вид прод-ии может быть взят или нет, то тогда задача будет иметь вид maxF= 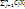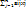≤ bi, Xj Є {0,1}, j=1,n
35) ЦП. Задача о назначении
Имеется n-исполнителей, кот. могут выполнять n-работ. Известна величина Cij, где i,j=1,n – это полезность i-го исполнителяб если он будет выполнять j-ю работу. Требуетя так назначить исполнителей на работы, чтобы добиться max-ной общей полезности при условии, что кажд. исполнитель может быть назначен только на одну работу и за каждой работой д.б. закреплен только 1 исполнитель. Обозначим через Xij=1 факт назначения i-го исполнителя на j-ю работу, а через Xij=0, факт неназначения, тогда ЭММ будет иметь вид: maxF= 
; 
=1, i=1,n; 
=1, j=1,n; Xij Є {0,1}, i,j=1,n Данная задача может использ-ся при закреплении автобусов за маршрутами, рабочих или бригад за работами и т.д.
36)Метод Гомори(метод отсеч-я)
Будем рассматривать следующую задачу целочис.програм-я
Max(min) F=∑ nj=1cijxij (1)
∑ nj=1cijxij =bi ,i=1,m (2)
xj≥0, j=1,n (3)
xj- целый, j=1,n (4)
Алгоритм метода:
1.Решается задача (1)-(3),с отброшенным усл-м целочис-ти(4).
2.Если усл.целочисленности вып-ся по всем переменным,то оптимальн.решение з-чи(1)-(4) совпад-т с оптимальн.решением з-чи(1)-(3).Если же это усл.не выпол-ся хотя бы поодной перемен-й,то переходим к шагу 3.Если з-ча(1)-(3)не разрешима,то и исходная з-ча не имеет реш-я.
3.Строится доп-ое ограничение,кот.отсекает часть ОДР,в кот.содерж-ся оптим-е решение з-чи (1)-(3) и не содер-ся ни одного допуст-го реш-я задачи(1)-(4)
4.Возвращ-ся к з-че с отброш-м условием целочисл-ти,но с расшир-й сис-мой осн-х ограничений.Добавляются огранич-я,построен-е на 3-ем шаге и вновь примен-ся симплексная процедура и т.д.
. Отличие выбора разрешающего элемента:
Сначала рассм-ся строка,в кот содерж-ся отриц-е число в столбце свободн.членов и рассмат-ем все неотриц-е числа в этой строке.Выбираем люб.отрицат.число,кот и будет определять разрешающ.столбец.Для чисел с один-ми знаками в столбце свободн.членов и разреш-м столбце наход-ся симплекс-е отношения.Наименьш.симплексн.отношение и определяет разреш-щую строку
