РАЗДЕЛ I. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Тема 1. Классификация событий
Случайные события. Полная группа событий. Классическое и статистическое определение вероятности. Свойства вероятности события. Элементы комбинаторики. Непосредственный подсчет вероятности. ([1], § 1.1—1.3, 1.5, 1.6).
При изучении этой темы студенты сталкиваются с такими фундаментальными понятиями как испытание (опыт, эксперимент), случайное событие, вероятность события и др. Необходимо четко представлять, что событие — это не какое-нибудь происшествие, а лишь возможный исход (результат) испытания, т.е. выполнение определенного комплекса условий.
Вероятность события есть численная мера степени объективной возможности наступления события. Если при классическом определении вероятность события определяется как доля случаев, благоприятствующих данному событию, то при статистическом определении — как доля тех фактически произведенных испытаний, в которых это событие появилось. При этом предполагается, что число испытаний достаточно велико, а события — исходы тех испытаний, которые могут быть воспроизведены неограниченное число раз при одном и том же комплексе условий, и обладают устойчивостью относительных частот. С теоретико-множественной трактовкой основных понятий и аксиоматическим построением теории вероятностей студент может ознакомиться по учебнику ([1], § 1.12). (Этот материал в обязательную программу не входит.)
Для решения задач на непосредственный подсчет вероятностей необходимо овладеть элементами комбинаторики, ([1], § 1,5) в первую очередь, определением числа сочетаний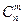 
(без повторений).
Тема 2. Основные теоремы
Сумма и произведение событий. Теорема сложения вероятностей и ее следствия. Зависимые и независимые события. Условная вероятность. Теорема умножения вероятностей для зависимых и независимых событий. Формулы полной вероятности и Байеса. ([1], § 1.7—1.11).
Студент должен четко усвоить основные операции над событиями — их сумму и произведение. Если (А + В) — событие, состоящее в появлении хотя бы одного из данных событий (т.е. наступления либо события А, либо события В, либо обоих событий вместе), то АВ представляет событие, состоящее в совместном появлении двух событий (т.е. наступления и события А, и события В). Нужно знать, что событием, противоположным сумме нескольких событий, является произведение противоположных событий, т.е.
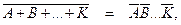
а событием, противоположным произведению нескольких событий, есть сумма противоположных событий:
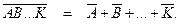
Основными теоремами данной темы являются теоремы сложения и умножения вероятностей. Следует четко знать, что вероятность суммы событий равна сумме их вероятностей (т.е. Р(А + В) =Р(А) +Р(В)) для несовместных событий, а вероятность произведения событий равна произведению их вероятностей (т.е. Р(АВ) =Р(А)Р(В)) для независимых
событий.
Завершают тему формулы полной вероятности и Байеса, являющиеся следствием теорем сложения и умножения вероятностей. Общим для этих формул является то, что они применяются в случае, когда данное событие F может произойти только при условии появления одной из гипотез А 1, А 2,…, Аn, образующих полную группу событий. Но если в формуле полной вероятности для P(F) ищется вероятность события F (безотносительно к рассматриваемой гипотезе), то формула Байеса позволяет произвести количественную переоценку априорных вероятностей гипотез Р(Аi) (i = 1, 2,..., п), известных до испытания, лишь после того, как событие F произошло, т.е. найти апостериорные (получаемые после проведения испытания) условные вероятности гипотез Р F (Аi).
Особое внимание следует уделить задачам по данной теме. Решение каждой из них должно сопровождаться предварительным логическим анализом условия, формулировкой и обозначением искомого события, выявлением его логической связи с другими, более простыми событиями. Этот анализ выявит применимость в данной задаче той или иной формулы или теоремы (теорем сложения, умножения, формул полной вероятности, Байеса и т.п.) и позволит обосновать дальнейшие операции, связанные с расчетом вероятностей.
При решении задачи прежде всего необходимо ввести обозначения для событий и по данным условия составить соотношения между ними, позволяющие определить искомую вероятность через данные или более просто определяемые вероятности. Нужно соблюдать условие применимости используемой теоремы (например, условие несовместности событий при использовании теоремы сложения, условие зависимости или независимости событий при использовании теоремы умножения и т.п.).
Тема 3. Повторные независимые испытания
Последовательность независимых испытаний. Формула Бернулли. Многоугольник распределения вероятностей. Асимптотическая формула Пуассона и условия ее применения. Локальная теорема Муавра—Лапласа. Функция f(x), ее свойства и график. Интегральная теорема Муавра—Лапласа и ее следствия. Функция Ф (х) Лапласа и ее свойства. ([1], § 2.1—2.4).
В этой теме рассматривается схема Бернулли — последовательность n независимых испытаний, в каждом из которых событие А может наступить с постоянной вероятностью Р(А) = р. Результат испытаний-появление т раз события А, которое чередуется в любом порядке с п – т раз непоявлением события А.
При этом могут определяться вероятности того, что:
а) событие А появится точно т раз (вероятность Рm,n);
б) событие А появится не менее или не более данного числа а раз (вероятности Pn(m ≥ a) или Рn(m ≤ a);
в) событие А появится т раз, заключенное в границах от а до b (включительно), т.е. вероятность Рn(a ≤ m ≤ b).
При решении задач темы следует уяснить, что нужно понимать под испытанием и событием А. Далее необходимо сформулировать вопрос задачи в виде условий, налагаемых на число т наступлений события или частость (относительную частоту) т/п. Затем перейти к записи условий задачи в терминах и обозначениях схемы повторных испытаний, к выбору подходящей расчетной формулы и вычислительной схемы.
Расчет вероятностей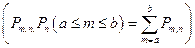 
можно производить по точной формуле Бернулли (если п — небольшое число) и по асимптотическим формулам, если п велико. Если по техническим причинам вероятность Рm,n не может быть вычислена по формуле Бернулли, то используются асимптотические формулы — формула Пуассона (если п — велико, р — мала, так, что λ= np ≤ 10), локальная формула Муавра—Лапласа (если 
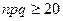). Если необходимо найти вероятность числа т (частости т/п) появления события, заключенного в некоторых пределах, то при условии 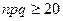может быть использована интегральная теорема Муавра—Лапласа и ее следствия.
Тема 4. Дискретные случайные величины
Понятие случайной величины и ее описание. Виды случайных величин. Дискретная случайная величина и ее закон (ряд) распределения; основное свойство закона распределения. Арифметические операции над случайными величинами. Биномиальный закон распределения и закон Пуассона. Математическое ожидание дискретной случайной величины и его свойства. Дисперсия и среднее квадратическое отклонение дискретной случайной величины. Математическое ожидание и дисперсия: а) случайной величины, распределенной по биномиальному закону и закону Пуассона; б) частости события в п независимых повторных испытаниях. ([1], § 3.1—3.4, 3.8, 4.1, 4.2).
В этой теме рассматривается одно из фундаментальных понятий теории вероятностей — понятие случайной величины. Под случайной величиной понимается переменная, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений (какое именно — заранее неизвестно). Если говорить более строго, то случайная величина есть функция, заданная на множестве элементарных исходов.
Наиболее полным описанием случайной величины является ее закон распределения, то есть всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
При решении задач случайная величина, как и случайное событие, подлежит четкому определению по условию. Ее связь со случайным событием заключается в том, что принятие ею некоторого числового значения (т.е. выполнение равенства Х = хi) есть случайное событие, характеризуемое вероятностью Р(Х = хi) = рi.
В данной теме рассматриваются дискретные случайные величины ( ДСВ ), характеризуемые конечным или бесконечным, но счетным множеством возможных значений хi и соответствующими им вероятностями рi=Р(X=хi). Большинство задач темы связано с построением для заданной случайной величины закона распределения, т.е. таблицы вида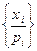 
. Решение подобных задач требует, прежде всего, четких определений случайной величины и испытания, количественный результат которого характеризуется значениями x1, x2,…, xi,…, xn.
Затем можно перейти к построению закона распределения случайной величины, а точнее — к вычислению вероятностей рi, как вероятностей событий Х = xi. Здесь могут быть использованы приемы и методы, рассмотренные при решении задач в темах 1 – 3.
Общая схема решения задач на построение законов распределения включает:
1) введение и четкое описание случайной величины, о которой идет речь;
2) описание множества ее возможных значений x1, x2,…, xi,…, xn;
3) рассмотрение выполнения каждого из равенств Х = хi как случайного события;
4) вычисление вероятностей этих событий с помощью основных теорем и формул;
5) проверка правильности составленного распределения с помощью
равенства 
.
Особое внимание следует обратить на числовые характеристики случайной величины, призванные в сжатой форме выразить наиболее существенные черты распределения, в частности, на математическое ожидание и дисперсию и их свойства.
Тема 5. Непрерывные случайные величины. Нормальный закон распределения
Функция распределения случайной величины, ее свойства и график. Определение непрерывной случайной величины. Вероятность отдельно взятого значения непрерывной случайной величины. Плотность вероятности, ее свойства и график. Математическое ожидание и дисперсия непрерывной случайной величины. Определение нормального закона распределения; теоретико-вероятностный смысл его параметров. Нормальная кривая и зависимость ее положения и формы от параметров. Функция распределения нормально распределенной случайной величины и ее выражение через функцию Лапласа. Формулы для определения вероятности: а) попадания нормально распределенной случайной величины в заданный интервал; б) отклонения нормально распределенной случайной величины от ее математического ожидания. Правило «трех сигм». Понятие о центральной предельной теореме (теореме Ляпунова). ([1], § 3.5—6.5).
Функция распределения случайной величины – одно из фундаментальных понятий теории вероятностей, поскольку является универсальным описанием любой случайной величины. Функция распределения F(x) представляет вероятность того, что случайная величина Х примет значение, меньшее х, т.е. F(x) = Р(Х < х). Необходимо знать свойства функции распределения F(x) и ее производной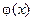 
— плотности вероятности случайной величины и уметь их изображать графически. Из непрерывных случайных величин особо важное значение имеет нормальный закон распределения. Необходимо знать теоретико-вероятностный смысл его параметров, выражение функции распределения FN(x) через функцию Лапласа Ф(х), свойства нормально распределенной случайной величины, правило «трех сигм». Важно четко представлять, что нормальный закон, в отличие от других, является предельным законом, к которому при некоторых весьма часто встречающихся условиях приводит совокупное действие (сумма) п независимых случайных величин X 1, X 2,…, Xn при 
.
Тема 6. Двумерные (n -мерные) случайные величины
Понятие двумерной (п-мерной) случайной величины. Одномерные распределения ее составляющих. Условные распределения. Ковариация и коэффициент корреляции. Свойства коэффициента корреляции. Двумерное нормальное распределение. Условные математическое ожидание и дисперсия. ([1], § 5.1, 5.6, 5.7).
В этой теме обобщается понятие случайной величины, вводится понятие многомерной (n -мерной) случайной величины, условных распределений и их числовых характеристик. Так как математические ожидания и дисперсии случайных величин Х и У недостаточно полно характеризуют двумерную случайную величину (X, Y), рассматриваются ковариация и коэффициент корреляции случайных величин, которые позволяют выявить степень зависимости между Х и Y. Завершается тема понятием двумерного нормального закона распределения. Следует обратить внимание на то, что в случае двумерного нормального закона зависимости условных математических ожиданий Мx(Y) (или My(x)) от х (или у), т. е. нормальные регрессии Y по Х (или Х по Y), всегда линейны, а условные дисперсии Dx(Y) (или Dy(X)) постоянны и не зависят от значений х (или у).
Тема 7. Закон больших чисел
Сущность закона больших чисел. Значение теорем закона больших чисел для математической статистики. Лемма Чебышева (неравенство Маркова). Неравенство Чебышева и его частные случаи: а) для средней арифметической случайных величин; б) для случайной величины, распределенной по биномиальному закону; в) для частости события. Теорема Чебышева и ее следствие. Теорема Бернулли. ([1], § 6.1–6.4).
Данная тема важна для понимания методов математической статистики. Она включает ряд теорем, устанавливающих при определенных условиях устойчивость частости (относительной частоты) и средней арифметической (теоремы Бернулли, Чебышева и др.). При изучении каждой из них важно уяснить условия их применимости, а также смысл утверждений, сопровождаемых словами «практически невозможно», «практически достоверно». Особое внимание следует уделить понятию «сходимости по вероятности».
При использовании неравенств Маркова и Чебышева в процессе решения задач необходимо учитывать, что:
1) приведенные неравенства дают не точное значение соответствующей вероятности, а лишь ее оценку снизу или сверху (вероятность не меньше (не больше) данного числа);
2) неравенство Чебышева оценивает вероятность отклонения случайной величины Х от ее математического ожидания M(X) = a.
Неравенство | X – a| может быть представлено в виде:
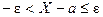или 
Это означает, что случайная величина Х принимает значения в границах, симметрично расположенных относительно а, т.е. от 
до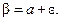 
РАЗДЕЛ 2. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Тема 8. Вариационные ряды
Вариационный ряд как результат первичной обработки данных наблюдений. Дискретный и интервальный ряды. Средняя арифметическая и дисперсия вариационного ряда. Упрощенный способ их вычисления. ([1], 8.1–8.4).
Прежде чем непосредственно изучать выборочный метод, необходимо ознакомиться с простейшей статистической обработкой опытных данных; построением вариационных рядов, вычислением их числовых характеристик.
Вариационный ряд является статистическим аналогом (реализацией) распределения признака (случайной величины), а его числовые характеристики – средняя арифметическая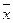 
и дисперсия s 2 – аналогами соответствующих числовых характеристик случайной величины – математического ожидания M (X) и дисперсии D (X). Точно так же понятие частости (относительной частоты) w для вариационного ряда аналогично понятию вероятности p для случайной величины.
Необходимо четко знать формулы вычисления числовых характеристик ряда (§ 8.2, 8.3). Более сложные формулы, используемые в упрощенном способе расчета (§ 8.4), являются вспомогательными, и их сложность объясняется переходом в расчетах от рассматриваемых вариантов к условным.
Однако некоторое усложнение нахождения числовых характеристик по этим формулам с лихвой компенсируется снижением трудоемкости расчетов за счет существенного упрощения условных вариантов по сравнению с исходными.
Тема 9. Основы выборочного метода
Сплошное и выборочное наблюдения. Генеральная и выборочная совокупности. Собственно-случайная выборка с повторным и бесповторным отбором членов. Репрезентативная выборка. Понятие об оценке параметров генеральной совокупности, свойства оценок: несмещенность, состоятельность и эффективность. Оценка генеральных доли и средней по собственно-случайной выборке. Несмещенность и состоятельность выборочных доли и средней. Смещенность и состоятельность выборочной дисперсии как оценки генеральной дисперсии. Интервальная оценка параметров. Доверительная вероятность, надежность оценки и предельная ошибка выборки. Формулы доверительных вероятностей для средней и доли. Объем выборки. ([1], § 9.1, 9.2, 9.4, 9.6).
Выборочный метод широко применяется на практике. Однако значение этой темы значительно шире, поскольку концепция выборки лежит в основе методологии математической статистики. Соотношение между характеристиками выборочной и генеральной совокупностей есть соотношение между опытными данными (результатами наблюдений) и теоретической моделью.
Чтобы по данным выборки иметь возможность судить о генеральной совокупности, она должна быть отобрана случайно. Поэтому выборочные характеристики – выборочные средняя 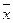, доля w и дисперсия s 2 – величины случайные в отличие от их аналогов в генеральной совокупности 
p и 
– величин неслучайных.
Необходимо знать свойства выборочных оценок: несмещенность, состоятельность, эффективность. Уметь обосновать несмещенность и состоятельность выборочных средней и доли. При этом следует помнить, что основное требование, предъявляемое к выборочной оценке 
заключается в том, чтобы ее рассеяние относительно оцениваемого параметра 
т.е. 
было минимальным. Для несмещенной оценки, для которой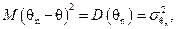 
это требование означает ее эффективность. Но даже «наилучшая» оценка является лишь приближенным значением неизвестного параметра и, будучи величиной случайной, может существенно отличаться от самого параметра.
Поэтому наряду с точечной рассматривают интервальную оценку параметра, т.е. такой числовой интервал, который с заданной доверительной вероятностью (надежностью) накрывает неизвестное значение параметра. Программой предусматривается построение доверительного интервала для генеральной средней и генеральной доли собственно-случайных выборок (повторной и бесповторной). Основой являются формулы доверительной вероятности для средней и доли ([1], (формулы (9.23), (9.24)).
Необходимо усвоить три типа задач на выборку, сводящиеся к определению предельной ошибки выборки или границ доверительного интервала, надежности оценки и объема выборки.
При решении задач на нахождение объема выборки следует учесть, что это не просто задачи на вычисление неизвестной величины n из формулы, выражающей предельную ошибку выборки через дисперсию признака. Ведь обычно объем выборки надо знать до проведения выборочного наблюдения, но в этом случае неизвестны не только дисперсии признака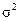 
или рq, но даже их оценки. Поэтому вместо неизвестных значений 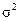или рq берут выборочные характеристики s 2 или w (1 – w) предшествующего исследования в аналогичных условиях, т.е. полагают, что 
Если никаких сведений о 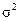или р нет, то в качестве 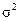или р используют их выборочные оценки по специальной пробной выборке небольшого объема и по формулам (9.33) – (9.36) находят объем основной выборки. При оценке генеральной доли р вместо проведения пробной выборки можно в формулах объема выборки произведение рq = р (1 – р) заменить его максимальным значением, равным 0,25.
Если по условию задачи объем бесповторной выборки значительно меньше объема генеральной совокупности или генеральная совокупность бесконечна, то расчет необходимых характеристик проводят по формулам для повторной выборки.
Тема 10. Элементы проверки статистических гипотез
Статистическая гипотеза и статистический критерий. Ошибки 1-го и 2-го рода. Уровень значимости и мощность критерия. Принцип практической уверенности. Оценка параметров законов распределения по выборочным данным. Понятие о критериях согласия.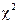 
- критерий Пирсона и схема его применения. ([1], § 10.1,10.2, 10.7).
Проверка статистических гипотез – один из наиболее часто используемых на практике разделов математической статистики. Необходимо усвоить также понятия как статистическая гипотеза и статистический критерий, ошибки 1-го и 2-го рода, уровень значимости и мощность критерия.
Важнейшим вопросом темы является построение теоретического закона распределения (выбор типа закона и оценка его параметров) по опытным данным и оценка его расхождения (согласия) с эмпирическим распределением. Необходимо уяснить суть критериев согласия, позволяющих установить (на данном уровне значимости), объясняется ли расхождение между эмпирическим и теоретическим распределением лишь случайными причинами, связанными с ограниченным числом наблюдений, или они являются существенными и связаны с тем, что теоретический закон распределения подобран неудачно.
Необходимо знать критерии согласия 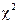-Пирсона и схему его применения.
Тема 11. Элементы теории корреляции
Функциональная, статистическая и корреляционная зависимости. Уравнения регрессии, корреляционная таблица. Групповые средние. Основные задачи теории корреляции: определение формы и оценка тесноты связи. Линейная парная регрессия. Определение параметров прямых регрессий методом наименьших квадратов. Выборочная ковариация. Формулы расчета коэффициентов регрессии. Выборочный коэффициент корреляции, его свойства и оценка достоверности (значимости). Понятие о нелинейной и множественной корреляции. ([1], § 12.1 – 12.3,12.5).
Корреляционный анализ наряду с выборочным методом представляет собой важнейшее прикладное направление математической статистики. Предметом его исследования является связь (зависимость) между различными варьирующими признаками (переменными величинами), при которой каждому значению одной переменной соответствует не определенное значение другой (как это имеет место при функциональной зависимости), а распределение другой переменной с определенным условным математическим ожиданием.
При изучении темы следует уяснить сущность статистической и ее частного случая – корреляционной зависимости.
Конечная цель корреляционного анализа – получение уравнений прямых регрессий, характеризующих форму зависимости, и вычисление коэффициента корреляции, определяющего тесноту (силу) связи, если она линейная.
Расчет производится в два основных этапа. На первом обрабатывают табличные данные для нахождения величин выборочных средних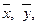 
дисперсий 
и выборочной ковариации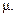 
При этом рекомендуется использовать упрощенный способ их расчета (§ 12.2). Второй этап – вычисление основных характеристик корреляционной зависимости – коэффициентов регрессии byx, bxy коэффициента корреляции r и оценка их достоверности.
При решении задачи 3 контрольной работы № 4 следует учесть, что прямые регрессии должны быть построены на одном чертеже с эмпирическими линиями (ломаными) регрессии, причем они должны образовывать с осью Оx либо только острые, либо только тупые углы и пересекаться в точке 
Все расчеты должны вестись с разумной степенью точности, используя правила приближенных вычислений, сохраняя в промежуточных вычислениях на 1-2 десятичных знака больше, чем в окончательном ответе (правило запасной цифры).
Вопросы для самопроверки
1. Классификация случайных событий. Классическое определение вероятности. Свойства вероятности события, непосредственный подсчет вероятности. Примеры.
2. Статистическое определение вероятности события и условия его применимости. Пример.
3. Несовместные и совместные события.Сумма событий. Теорема сложения вероятностей (с доказательством). Пример.
4. Полная группа событий. Противоположные события. Соотношение между вероятностями противоположных событий (с выводом). Примеры.
5. Зависимые и независимые события. Произведение событий. Понятие условной вероятности. Теорема умножения вероятностей (с доказательством). Примеры.
6. Формулы полной вероятности и Байеса (с доказательством). Примеры.
7. Повторные независимые испытания. Формула Бернулли (с выводом). Примеры.
8. Локальная теорема Муавра—Лапласа, условия ее применимости. Свойства функции f(x). Пример.
9. Асимптотическая формула Пуассона и условия ее применимости.
Пример.
10. Интегральная теорема Муавра—Лапласа и условия ее применимости. Функция Лапласа Ф (х) и ее свойства. Пример.
11. Следствия из интегральной теоремы Муавра—Лапласа (с выводом). Примеры.
12. Понятие случайной величины и ее описание. Дискретная случайная величина и ее закон (ряд) распределения. Независимые случайные величины. Примеры.
13. Математические операции над дискретными случайными величинами и примеры Построения законов распределения для kХ, Х2, Х+Y, XY по заданным распределениям независимых случайных величин Х и Y.
14. Математическое ожидание дискретной случайной величины и его свойства (с выводом). Примеры.
15. Дисперсия дискретной случайной величины и ее свойства (с выводом). Примеры.
16. Математическое ожидание и дисперсия числа и частости наступлений события в п повторных независимых испытаниях (с выводом).
17. Случайная величина, распределенная по биномиальному закону, ее математическое ожидание и дисперсия. Закон распределения Пуассона.
18. Функция распределения случайной величины, ее определение, свойства и график.
19. Непрерывная случайная величина (НСВ). Вероятность отдельно взятого значения НСВ. Математическое ожидание и дисперсия НСВ.
20. Плотность вероятности непрерывной случайной величины, ее определение, свойства и график.
21. Определение нормального закона распределения. Теоретико-вероятностный смысл его параметров. Нормальная кривая и зависимость ее положения и формы от параметров.
22. Функция распределения нормально распределенной случайной величины и ее выражение через функцию Лапласа.
23. Формулы для определения вероятности: а) попадания нормально распределенной случайной величины в заданный интервал; б) ее отклонения от математического ожидания. Правило трех сигм.
24. Центральная предельная теорема. Понятие о теореме Ляпунова и ее значение. Пример.
25. Понятие двумерной (n -мерной) случайной величины. Примеры. Таблица ее распределения. Одномерные распределения ее составляющих. Условные распределения и их нахождение по таблице распределения.
26. Ковариация и коэффициент корреляции случайных величин. Связь между некоррелированностью и независимостью случайных величин.
27. Понятие о двумерном нормальном законе распределения. Условные математические ожидания и дисперсии.
28. Неравенство Маркова (лемма Чебышева) (с выводом). Пример.
29. Неравенство Чебышева (с выводом) и его частные случаи для случайной величины, распределенной по биномиальному закону, и для частости события.
30. Неравенство Чебышева для средней арифметической случайных величин (с выводом).
31. Теорема Чебышева (с доказательством), ее значение и следствие. Пример.
32. Закон больших чисел. Теорема Бернулли (с доказательством) и ее значение. Пример.
33. Вариационный ряд, его разновидности. Средняя арифметическая и дисперсия ряда. Упрощенный способих расчета.
34. Генеральная и выборочная совокупности. Принцип образования выборки. Собственно-случайная выборка с повторным и бесповторным отбором членов. Репрезентативная выборка. Основная задача выборочного метода.
35. Понятие об оценке параметров генеральной совокупности. Свойства оценок: несмещенность, состоятельность, эффективность.
36. Оценка генеральной доли по собственно-случайной выборке. Несмещенность и состоятельность выборочной доли.
37. Оценка генеральной средней по собственно-случайной выборке. Несмещенность и состоятельность выборочной средней.
38. Оценка генеральной дисперсии по собственно-случайной выборке. Смещенность и состоятельность выборочной дисперсии (без вывода). Исправленная выборочная дисперсия.
39. Понятие об интервальном оценивании. Доверительная вероятность и доверительный интервал. Предельная ошибка выборки. Ошибки репрезентативности выборки (случайные и систематические).
40. Формула доверительной вероятности при оценке генеральной доли признака. Средняя квадратическая ошибка повторной и бесповторной выборок и построение доверительного интервала для генеральной доли признака.
41. Формула доверительной вероятности при оценке генеральной средней. Средняя квадратическая ошибка повторной и бесповторной выборок и построение доверительного интервала для генеральной средней.
42. Определение необходимого объема повторной и бесповторной выборок при оценке генеральной средней и доли.
43. Статистическая гипотеза и статистический критерий. Ошибки 1-го и 2-го рода. Уровень значимости и мощность критерия. Принцип практической уверенности.
44. Построение теоретического закона распределения по опытным данным. Понятие о критериях согласия.
45. Критерий согласия 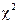- Пирсона и схема его применения.
46. Функциональная, статистическая и корреляционная зависимости. Различия между ними. Основные задачи теории корреляции.
47. Линейная парная регрессия. Система нормальных уравнений для определения параметров прямых регрессии. Выборочная ковариация. Формулы для расчета коэффициентов регрессии.
48. Оценка тесноты связи. Коэффициент корреляции (выборочный), его свойства и оценка достоверности.
Задачи для самоподготовки
Ниже приводятся номера рекомендуемых задач с решениями и для самостоятельного выполнения по учебнику [1]. Студентам рекомендуется в первую очередь разобрать задачи с решениями, а затем выборочно решать задачи для самостоятельного выполнения (например, каждую вторую задачу из списка задач по теме).
| № п/п | Название темы | Номера задач по учебнику [1] | |
| с решениями | для самостоятельного выполнения | ||
| РАЗДЕЛ I. ТЕОРИЯ ВЕРОЯТНОСТЕЙ | |||
| Классификация событий | 1.1, 1.10 – 1.16 | 1.37 – 1.49 | |
| Основные теоремы | 1.17 – 1.31, 1.34 – 1.35 | 1.53 – 1.78 | |
| Повторные независимые испытания | 2.1 – 2.12 | 2.13 – 2.34 | |
| Дискретные случайные величины | 3.1 – 3.10, 3.18, 3.19а, 3.20 – 3.22, 4.1, 4.2, 4.5 | 3.25 – 3.46, 3.49 – 3.61, 4.11 – 4.16 | |
| Непрерывные случайные величины | 3.11 – 3.14, 3.24, 4.9 | 3.47, 3.48, 3.62 – 3.66, 4.19 – 4.23 | |
| Двумерные (n -мерные) случайные величины | 5.2, 5.5 | 5.10, 5.14 | |
| Закон больших чисел | 6.1 – 6.4, 6.6 – 6.8 | 6.9 – 6.22 | |
| РАЗДЕЛ II. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА | |||
| Вариационные ряды | 8.2, 8.3, 8.6, 8.8 | 8.10 – 8.12 | |
| Основы выборочного метода | 9.6, 9.7, 9.10 – 9.13 | 9.19 – 9.27, 9.30 | |
| Элементы проверки статистических гипотез | 10.12 | 10.28 – 10.30 | |
| Элементы теории корреляции | 12.1 – 12.6 | 12.14 – 12.18 |
Указания по выполнению контрольных работ
В соответствии с учебным планом по дисциплине «Теория вероятностей и математическая статистика» каждый студент должен выполнить две контрольные работы — № 3 и №4. Контрольная работа №3 охватывает материал курса, соответствующий разделу «Теория вероятностей», а контрольная работа №4 — материал раздела «Математическая статистика».
Обе контрольные работы (№ 3 и № 4) все студенты вечерних и дневных групп выполняют дома по приведенным в данном пособии вариантам и направляют в институт для проверки в сроки, указанные в индивидуальном графике студента. Однако эти сроки являются крайними. Поэтому, чтобы работа была своевременно проверена, при необходимости доработана и сдана повторно, ее надлежит выслать значительно раньше указанного срока.
Студентам дневных групп рекомендуется во время установочной (зимней экзаменационной) сессии вчерне выполнить домашнюю контрольную работу №3 (№4), чтобы получить консультацию по возникшим в ходе написания работы вопросам. В течение двух недель после окончания сессии соответствующая работа должна быть завершена и представлена на проверку.
Если работа имеет существенные недочеты и требуется повторное решение задач, то она получает оценку «Не допускается к собеседованию». Такую работу в той же тетради, если есть место, или новой необходимо переделать в соответствии с указаниями преподавателя, проверявшего работу. Новая работа с надписью «Повторная» вместе с первоначальной направляется для повторной проверки. На обложке тетради необходимо указать фамилию преподавателя, которым работа ранее не была зачтена.
Если работа оценивается положительно, на ней делается запись «Допускается к собеседованию». При этом в работе могут быть отдельные недочеты или ошибки, которые следует устранить. Работу над ошибками необходимо представить на собеседовании.
Собеседование проходят все студенты по каждой контрольной работе, оцененной положительно. Время проведения собеседования устанавливается территориальным подразделением (филиалом). Если со студентом дневной группы собеседование не проводилось в межсессионный период, оно будет проведено во время экзаменационной сессии. В ходе собеседования проверяется самостоятельность выполнения работы, выявляется знание основных теоретических положений учебно – программного материала, охватываемого данной работой.
По результатам собеседования ставится зачет или незачет. К экзамену допускаются только те, студенты которые успешно прошли собеседование по двум контрольным работам (№ 3 и № 4).
Замечание. В соответствии с учебным планом по дисциплине «Теория вероятностей и математическая статистика» может быть предусмотрено компьютерное тестирование. В этом случае дополнительным обязательным условием допуска к экзамену является положительная оценка студентов на тестировании.
Основные требования к выполнению и оформлению контрольной работы
Прежде, чем приступить к решению задачи, необходимо переписать ее условие, а затем после слова «Решение» привести решение, к каждому этапу которого должны быть даны развернутые объяснения, описание вводимых обозначений. Используемые формулы и теоремы должны записываться с необходимыми пояснениями. Окончательный ответ следует выделить и сформулировать словесно.
Все расчеты нужно проводить тщательно с учетом правил приближенных вычислений[1]. Учитывая, что используемые при решении задач таблицы четырехзначные, все промежуточные вычисления следует проводить с четырьмя верными знаками после запятой, а окончательный ответ дать с тремя верными знаками, правильно округлив полученный до этого результат.
При выполнении громоздких расчетов, связанных с обработкой вариационных рядов и корреляционных таблиц, рекомендуется пользоваться упрощенной схемой вычислений ([1], § 8.4, § 12.2). Прежде чем приступить к решению задачи 2 контрольной работы № 4, ознакомьтесь с замечанием, приведенном в учебнике ([1], § 10.7).
В конце работы указывается список использованной литературы, ставится дата окончания работы и подпись. Поля в тетради, где выполняется работа, должны быть не менее 3 см.
Зачетные контрольные работы хранятся у студента и обязательно предъявляются на экзамене. В случае успешной сдачи экзамена эти работы остаются у экзаменатора.
Ниже приведены варианты заданий контрольных работ № 3 и № 4. Индивидуальный номер варианта соответствует последней цифре номера личного дела студента, который совпадает с номером зачетной книжки и студенческого билета.
Контрольная работа не рассматривается, если ее вариант не совпадает с последней цифрой номера личного дела студента или она выполнена по вариантам прошлых лет.
ВАРИАНТЫ КОНТРОЛЬНЫХ РАБОТ[2]
ВАРИАНТ 1
(для студентов, номера личных дел которых оканчиваются цифрой 1)
онтрольная работа №3
1. В первом ящике 2 красных и 5 синих папок, во втором – 4 красных и 3 синих. Из первого ящика переложили 2 папки во второй, после чего из второго ящика наудачу достали одну папку. Какова вероятность того, что она красного цвета?
2. Вероятность сдачи студентом контрольной работы в срок равна 0,7. Найти вероятность того, что из 5 студентов вовремя сдадут контрольную работу:
а) ровно 3 студента; б) хотя бы один студент.
3. Всхожесть хранящегося на складе зерна равна 80%. Отбираются 400 зерен. Определить вероятность того, что из отобранных зерен взойдут:
а) ровно 303; б) от 250 до 330.
4. Котировки акций могут быть размещены в Интернете на трех сайтах. Материал есть на первом сайте с вероятностью 0,7, на втором – с вероятностью 0,6, на третьем – с вероятностью 0,8. Студент переходит к новому сайту только в том случае, если не найдет данных на предыдущем. Составить закон распределения числа сайтов, которые посетит студент.
Найти:
а) функцию распределения этой случайной величины и построить ее график;
б) математическое ожидание и дисперсию этой случайной величины.
5. Случайная величина Х имеет нормальный закон распределения с параметрами а и 
.
Найти:
а) параметр , если известно, что математическое ожидание М (Х)=5 и вероятность 
б) вероятность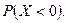 
онтрольная работа №4
1. Для проверки качества поступившей партии зерна по схеме собственно-случайной бесповторной выборки произведено 10%-ное обследование. В результате анализа установлено следующее распределение данных о влажности зерна:
| Процент влажности | Менее 8 | 8–10 | 10–12 | 12–14 | 14–16 | 16– –18 | 18– –20 | Более 20 | Итого |
| Число проб |
Найти: а) вероятность того, что средний процент влажности зерна в партии отличается от ее среднего процента в выборке не более чем на 0,5% (по абсолютной величине); б) границы, в которых с вероятностью 0,95 заключена доля зерна, влажность которого менее 12%; в) объем выборки, при которой те же границы для доли зерна, полученные в пункте б), можно гарантировать с вероятностью 0,9876; дать ответ на тот же вопрос, если никаких предварительных данных о рассматриваемой доле нет.
2. По данным задачи 1, используя 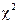-критерий Пирсона, на уровне значимости a = 0,05 проверить гипотезу о том, что случайная величина X – процент влажности зерна – распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.
3. Распределение 60 предприятий по затратам рабочего времени X (тыс. человеко-дней (чел. дн.)) и выпуску продукции Y (млн. руб.) представлены в таблице:
 y
x
| 30–40 | 40–50 | 50–60 | 60–70 | 70–80 | Итого: |
| 10–25 | ||||||
| 25–40 | ||||||
| 40–55 | ||||||
| 55–70 | ||||||
| 70–85 | ||||||
| Итого: |
Необходимо:
1) Вычислить групповые средние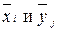 
, построить эмпирические линии регрессии;
2) Предполагая, что между переменными X и Y существует линейная корреляционная зависимость: а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений; б) вычислить коэффициент корреляции; на уровне значимости a = 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными X и Y; в) используя соответствующее уравнение регрессии, оценить средний выпуск продукции предприятия с затратами рабочего времени 55 тыс. чел. дн.
ВАРИАНТ 2
(для студентов, номера личных дел которых оканчиваются цифрой 2)
онтрольная работа №3
1. Дано восемь карточек с буквами Н, М, И, И, Я, Л, Л, О. Найти вероятность того, что:
а) получится слово «ЛОМ», если наугад одна за другой выбираются три карточки и располагаются в ряд в порядке появления;
б) получится слово «МОЛНИЯ», если наугад одна за другой выбираются шесть карточек.
2. По телевидению с 1 сентября начинают показывать 4 новых сериала. Вероятность того, что сериал продлится до Нового года, равна 0,3. Найти вероятность того, что до Нового года из этих сериалов продлится:
а) ровно 2; б) хотя бы один.
3. В филиале института 1000 студентов. После окончания занятий в среднем каждый десятый студент занимается в читальном зале. Сколько посадочных мест нужно иметь, чтобы с вероятностью 0,9545 их хватало всем студентам филиала.
4. Законы распределения независимых случайных величин X и Y приведены в таблицах:
| |||
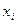
| 0,1 | ? | 0,7 |
| ||
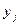
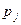
| 0,6 | ? |
X: Y:
Найти:
а) вероятност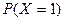и 
и 
б) закон распределения случайной величины 
в) математическое ожидание 
и дисперсию D(Z);
г) функцию распределения 
5. Уровень воды в реке – случайная величина со средним значением 2,5 м и стандартным отклонением 20 см. Оценить вероятность того, что в наудачу выбранный день уровень воды:
а) превысит 3 м; б) окажется в пределах от 2м 20см до 2м 80см.
онтрольная работа №4
1. По схеме собственно-случайной бесповторной выборки проведено 5%-ное обследование вкладов в Сбербанк одного из городов. Результаты обследования 150 вкладов представлены в таблице:
| Размер вклада, тыс. руб. | Менее 40 | 40–60 | 60–80 | 80–100 | 100– –120 | 120– –140 | Более 140 | Итого: |
| Число вкладов |
Найти: а) вероятность того, что средний размер всех вкладов в Сбербанке отличается от их среднего размера в выборке не более чем на 5 тыс. руб. (по абсолютной величине); б) границы, в которых с вероятностью 0,95 заключена доля вкладов, размер которых менее 80 тыс. руб.; в) объем выборки, при которой те же границы для доли вкладов, полученные в пункте б), можно гарантировать с вероятностью 0,9876; дать ответ на тот же вопрос, если никаких предварительных данных о рассматриваемой доле нет.
2. По данным задачи 1, используя 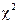-критерий Пирсона, на уровне значимости a = 0,05 проверить гипотезу о том, что случайная величина X – размер вклада – распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.
3. Распределение 50 предприятий по стоимости основных производственных фондов X (млн. руб.) и стоимости произведенной продукции Y (млн. руб.) представлены в таблице:
 y
x
| 15–20 | 20–25 | 25–30 | 30–35 | 35–40 | 40–45 | Итого: |
| 20–30 | |||||||
| 30–40 | |||||||
| 40–50 | |||||||
| 50–60 | |||||||
| 60–70 | |||||||
| Итого: |
Необходимо:
1) вычислить групповые средние 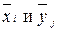и построить эмпирические линии регрессии;
2) предполагая, что между переменными X и Y существует линейная корреляционная зависимость: а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений; б) вычислить коэффициент корреляции; на уровне значимости a = 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными X и Y; в) используя соответствующее уравнение регрессии, определить среднюю стоимость произведенной продукции, на предприятиях со стоимостью основных производственных фондов 45 млн. руб.
ВАРИАНТ 3
(для студентов, номера личных дел которых оканчиваются цифрой 3)
онтрольная работа №3
1. Студент пришел на зачет, зная 24 вопроса из 30. Какова вероятность сдать зачет, если для получения зачета необходимо ответить на один вопрос, а преподаватель задает последовательно не более двух вопросов.
2. В среднем 10% заключенных в городе браков в течение года заканчиваются разводом. Какова вероятность того, что из четырех случайно отобранных пар, заключивших брак, в течение года:
а) ни одна пара не разведется; б) разведутся не более двух пар.
3. Вероятность того, что желание, загаданное на Новый год, сбудется, равна 0,7. Найти вероятность того, что из 200 загаданных желаний сбудется:
а) ровно 140; б) от 120 до 150.
4. Дискретная случайная величина Х задана функцией распределения:
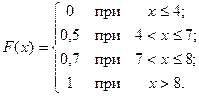
Найти:
а) ряд распределения случайной величины Х;
б) дисперсию D (Х);
в) вероятность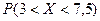 
.
5. Дневная выручка магазина является случайной величиной со средним значением 10000 руб. и средним квадратическим отклонением 2000 руб.
1) С помощью неравенства Чебышева оценить вероятность того, что дневная выручка будет находиться в пределах от 6000 до 14000 руб.
2) Найти вероятность того же события, учитывая, что дневная выручка магазина является случайной величиной, распределенной по нормальному закону.
3) Объяснить различие результатов.
онтрольная работа №4
1. По схеме собственно-случайной бесповторной выборки проведено 10%-ное обследование предприятий одной из отраслей экономики в отчетном году. Результаты обследования представлены в таблице:
| Выпуск продукции, млн.руб. | Менее 30 | 30– –40 | 40– –50 | 50– –60 | 60– –70 | 70– –80 | 80– –90 | Более 90 | Итого: |
| Число предприятий |
Найти: а) вероятность того, что средний размер выпуска продукции всех предприятий отличается от его среднего размера в выборке не более чем на 5 млн. руб. (по абсолютной величине); б) границы, в которых с вероятностью 0,95 заключена доля предприятий, выпуск продукции которых менее 50 млн. руб.; в) объем выборки, при которой те же границы для доли предприятий, полученные в пункте б), можно гарантировать с вероятностью 0,9876; дать ответ на тот же вопрос, если никаких предварительных данных о рассматриваемой доле нет.
2. По данным задачи 1, используя 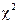-критерий Пирсона, на уровне значимости a = 0,05 проверить гипотезу о том, что случайная величина X –объем выпуска продукции – распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.
3. Распределение 50 российских коммерческих банков по объему вложений в ценные бумаги X (тыс. руб.) и полученной прибыли Y (тыс. руб.) представлены в таблице:
 y
x
| 100–120 | 120–140 | 140–160 | 160–180 | 180–200 | 200–220 | Итого: |
| 1000–1300 | |||||||
| 1300–1600 | |||||||
| 1600–1900 | |||||||
| 1900–2200 | |||||||
| 2200–2500 | |||||||
| Итого: |
Необходимо:
1) вычислить групповые средние 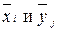и построить эмпирические линии регрессии;
2) предполагая, что между переменными X и Y существует линейная корреляционная зависимость: а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений; б) вычислить коэффициент корреляции; на уровне значимости a = 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными X и Y; в) используя соответствующее уравнение регрессии, оценить среднюю прибыль, полученную коммерческим банком, вложившим в ценные бумаги 1500 тыс. руб.
ВАРИАНТ 4
(для студентов, номера личных дел которых оканчиваются цифрой 4)
онтрольная работа №3
1. На школьном участке посадили три плодовых дерева: яблоню, грушу и сливу. Вероятность того, что приживется яблоня, равна 0,8, груша – 0,9, слива – 0,7. Найти вероятность того, что
а) приживутся два дерева; б) приживется хотя бы одно дерево.
2. В семье пять детей. Найти вероятность того, что среди них:
а) два мальчика; б) более двух мальчиков;
в) не менее двух и не более трех мальчиков.
Вероятность рождения мальчика принять равной 0,51.
3. Сколько раз надо подбросить симметричную монету, чтобы с вероятностью 0,9 частость проявления герба отличалась от его вероятности не более, чем на 0,01 (по абсолютной величине)?
4. Имеются 10 билетов: 1 билет в партер стоимостью 500 руб., 3 билета в амфитеатр по 300 руб. и 6 билетов на балкон по 100 руб. После реализации части билетов осталось три билета. Составить закон распределения случайной величины Х – стоимости непроданных билетов. Найти математическое ожидание 
5. Плотность вероятности случайной величины Х имеет вид:
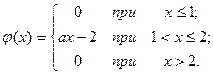
Найти:
а) параметр а; б) функцию распределения F (x) и построить ее график.
Что вероятнее: попадание случайной величины в интервал (1,6; 1,8) или в интервал (1,9; 2,6)?
онтрольная работа №4
1. Данные об урожайности зерновых культур в некотором регионе получены с помощью собственно-случайной бесповторной выборки. Результаты обследования 100 предприятий из 1000 приведены в таблице:
| Урожайность, ц/га | 20– –30 | 30– –40 | 40– –50 | 50– –60 | 60– –70 | 70– –80 | 80– –90 | 90– –100 | Итого: |
| Число предприятий |
Найти: а) границы, в которых с вероятностью 0,9643 заключена средняя урожайность зерновых культур для всех предприятий региона; б) вероятность того, что доля всех предприятий, урожайность зерновых культур в которых менее 50 ц/га, отличается от доли таких предприятий в выборке не более, чем на 5% (по абсолютной величине); в) объем выборки, при котором границы для средней урожайности, найденные в пункте а), можно гарантировать с вероятностью 0,9807.
2. По данным задачи 1, используя 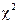-критерий Пирсона, на уровне значимости a = 0,05 проверить гипотезу о том, что случайная величина X – урожайность зерновых культур – распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.
3. Распределение 80 литейных цехов машиностроительных заводов по степени компьютеризации процессов производства X (%) и производственным затратам Y (млн. руб.) представлено в таблице:
| y
x
| 5–6 | 6–7 | 7–8 | 8–9 | 9–10 | Итого: | |||||||||||
| 10–20 | |||||||||||||||||
| 20–30 | |||||||||||||||||
| 30–40 | |||||||||||||||||
| 40–50 | |||||||||||||||||
| 50–60 | |||||||||||||||||
| 60–70 |
<
Дата добавления: 2017-02-11; Мы поможем в написании ваших работ!; просмотров: 889 | Нарушение авторских прав Поиск на сайте: Лучшие изречения:  | 2363 -  |
Ген: 0.011 с.