илет 8.
Для доказательства будем пользоваться 3-мя звеньями.
При последовательном соединении:
xвх->W1(p)->y1->W2(p)->y2->W3(p)->y
y1=W1(p)xвх
y2=W2(p)y1=W2(p)W1(p)xвх
y=W3(p)W2(p)W1(p)xвх
При параллельном соединении:
y=y1+y2+y3=W1(p)xвх+W2(p)xвх+W3(p)xвх=xвх(W1(p)+ W2(p)+ W3(p))
При встречно-параллельном соединении (обратная связь):
y=Wп(p)xвх±Wп(p)yос=Wп(p)xвх±Wп(p)Wос(p)y
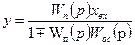
Билет 9.
(pE-A)-1 – характеристический многочлен матрицы A.
Билет 10.
САУ полностью управляема, если при помощи управляющего воздействия y(t) её можно перевести из состояния x(t0) в состояние x(t1) за конечный промежуток времени принадлежащий интервалу t0..t1.
САУ полностью наблюдаема, если при помощи измерения выходной переменной y(t) возможно определить все её переменные состояния x(t).
M = [B, AB, A2B,…, An-1B], (n, n*m)
L = [CT, ATCT, (AT)2CT, …(AT)n-1CT], (n, n*l)
A,B,C – из системы билета 9.
Если rang(M)=n – система управляема.
Если rang(L)=n – система наблюдаема.
Билет 11.
X.=Ax+Bu è получение передаточной функции.
Билет 12.
етод 1. Линеаризация разложением в ряд Тейлора около опорного движения или траектории.
1. На основании изучения физических свойств определяется размерность системы (число независимых переменных), составляются дифференциальные уравнения системы/ее звеньев.
2. Определяется рабочая точка установившегося режима работы звена системы, в которой требуется определить поведение звена/системы при малых отклонениях от установившегося значения координат состояния (x0,y0).
3. Несущественно-нелинейные звенья (аналитические) разлагаются в ряд Тейлора в окрестности рабочей точки (x0,y0).
В результате этих действий САУ в переходном и установившемся режиме (x, y) мало отклоняется от заданных программных (x0,y0).
Пример:
етод 2. Использование метода наименьших квадратов.
Метод применяется для определения неизвестных коэффициентов линейных моделей.
Пример:
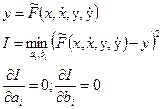
Линеаризация используется для:
· определения грубых законов в нелинейных системах управления;
· для получения законов управления в адаптивных системах.
Билет 13.
Устойчивость – свойство САУ возвращаться в заданный или близкий ему установившийся режим после какого-либо воздействия.
САУ устойчива, если переходные процессы в ней затухающие, выходная величина является ограниченной при условии, что входная величина также ограничена.
yвын представляет собой частное решение дифференциального уравнения, является установившейся величиной, yвын = const.
yсвоб является общим решением дифференциального уравнения:
Затухание переходного процесса зависит от вида корней pi. Учтем, что pè∞.
· Если pi – вещественное: в случае отрицательного значения Ciepit – стремится к 0 – затухает, в случае положительного значения – расходится.
· Если pi – комплексная величина, то при решении характеристического уравнения существует сопряженная с ней величина:
Если α<0, то процесс затухает, если α>0 – расходится, α=0 – гармонические колебания.
Билет 14.
Теоремы Ляпунова:
1. Если все вещественные части корней характеристического уравнения линеаризованной системы отрицательны, то линеаризованная система устойчива. Её невозмущенные движения асимптотически устойчивы и никакие добавки в виде членов с различными нелинейностями не смогут сделать систему неустойчивой.
2. Если по крайней мере один корень линеаризованной системы содержит положительную вещественную часть, то система неустойчива.
3. Если вещественные части корней характеристического уравнения линеаризованной системы равны 0, то свойство устойчивости линеаризованной системы будет неопределенным (система на границе устойчивости).
Билет 15.
Критерий устойчивости Гурвица:
Пусть D(p) = a0pn + a1pn-1 + … + an, тогда:
- определитель Гурвица
Для того, чтобы система была устойчива необходимо и достаточно, чтобы ∆n и все его миноры были положительны при a0>0.
Билет 16.
Критерий устойчивости Михайлова:
p=iw, w – угловая частота колебаний [0.. ∞).
D(iw)=…D(w)eiφ(w) = 0
D(p)=a0(p-p1)(p-p2)…(p-pn)
D(iw)= a0(iw-p1)(iw-p2)…(iw-pn)
Каждая из скобок представляет собой комплексное число, а при перемножении аргументы комплексных чисел складываются. Рассмотрим отдельно одну из скобок.
· Если pi – положительное вещественное число, то при wè∞ опишется угол -П/2.
· Если pi – отрицательное вещественное число, то при wè∞ опишется угол П/2.
· Если pi – комплексное число, то существует сопряженное с ним pi+1; суммарный угол поворота составит -2П/2, если вещественная часть корней положительна или 2П/2 в обратном случае.
l – число корней с положительной вещественной частью; (n-l) – число корней с отрицательной вещественной частью (n – общее число корней, порядок системы), тогда общий угол поворота составит: φ = -Пl/2 + (n-l)П/2 = nП/2 - lП
Для того, чтобы все вещественные части корней были отрицательны требуется, чтобы суммарный угол поворота составил nП/2, т.е. для устойчивости линейной системы n порядка необходимо и достаточно, чтобы D(iw), описывающий кривую Михайлова при изменении w от 0 до ∞ имел общий угол nП/2.
Кривая Михайлова для устойчивой системы имеет спиралевидную форму, причем е1 конец уходит в бесконечность в квадранте, номер которого равен порядку системы, причем порядок прохождения квадрантов не должен нарушаться (должно происходить чередование корней).
Наличие границ устойчивости определяется так:
· Нулевой корень (1 тип): годограф выходит из (0,0).
· Колебательная граница (2 тип): годограф проходит через (0,0).
· Бесконечный корень (3 тип): a0 будет проходить через 0-е значение, меняя знак с + на -.
Билет 17.
Рассмотрим динамическое звено при подаче на его вход гармонического сигнала x1(t)=X1cos(wt)=X1(eiwt+ e-iwt)/2=x1’+x1’’. При этом на его выходе также (из-за линейности системы) будет гармоническая функция x2(t)=X2cos(wt+u)=X2(eiwt+u+ e-iwt-u)/2=x2’+x2’’, сдвинутая относительно входной на u. За счет принципа суперпозиции можно считать: x1’àx2’, x1’’àx2’’. В расчетах будем учитывать только первую пару.
Полученное выражение называется частотной передаточной функцией звена. Оно может быть получено из обычной передаточной функции путем замены p=iw.
Частотная передаточная функция есть преобразование Фурье его функции веса:
, где A(w) – модуль чпф, равен отношению амплитуд выходной величины к входной;
u – сдвиг фаз между выходом и входом.
A(w) – амплитудная фазовая характеристика.
u(w) – частотная фазовая характеристика.
Билет 18.
Критерий Найквиста:
Рассмотрим передаточную функцию звена Wр(p), соответствующего устойчивой статической системе, не содержащего в знаменателе p в качестве множителя, т.е. с полюсами в левой полуплоскости.
Введем новую передаточную функцию: 
, причем степень R меньше степени Q. D(p) – характеристический полином системы.
Определим частотную передаточную функцию: W(iw)=D(iw)/Q(iw) и построим годограф при w= -∞..∞. Определим изменение аргумента данного выражения. Если все корни характеристического уравнения находятся в левой полуплоскости, то суммарный угол поворота числителя составит n*П (по аналогии с кривой Михайлова, но там nП/2 и w = 0..∞). Аналогично получим для числителя (степени числителя и знаменателя равны). Учтем, что при делении аргументы комплексных величин вычитаются, т.е. суммарный угол поворота равен 0 и годограф не охватывает начало координат.
Так как вспомогательная передаточная функция W(p) отличается от исходной Wр(p) на единицу, то условие охвата переносится на точку (-1,0i).
Абсолютная устойчивость, условная устойчивость, граница устойчивости, неустойчивость.
При наличии в знаменателе множителя p поступают следующим образом: относят его к левой полуплоскости и обходят справа окружностью бесконечно малого радиуса. В этом случае pà0, радиус к ∞, а аргумент совершает скачок на П, т.е. при этом на годографе присутствует полуокружность бесконечно большого радиуса. Для множителя p2 будет окружность бесконечно большого радиуса, для пары число мнимых корней произойдет скачок на П. Во всех случаях окружности бб радиуса идет по часовой стрелке.
Обобщенный критерий Найквиста: если в разомкнутом состоянии система имеет l корней в правой полуплоскости, то для того, чтобы замкнутая система была устойчивой требуется, чтобы годограф охватывал точку (-1, i0) углом 2lП против часовой стрелки.
Билет 19.
Логарифмические частотные характеристики.
Прологарифмируем частотную АФХЧ. 
. На практике применяется lg, при этом:
логарифмическая амплитудная характеристика: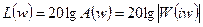 
. Измеряется в децибелах (1 дб – изменение амплитуды в 
).
При построении используется логарифмическая координатная сетка. По оси абсцисс откладывается w, по оси ординат L(w) и логарифмическая фазовая характеристика.
Билет 20.
По логарифмическим частотным характеристикам можно определять устойчивость замкнутой системы. Условия нахождения на границе устойчивости: ln|W(iw)|=0, u(w)=arg(W(iw))=-П.
Графически это представимо следующим образом: если лах проходит ось абсцисс левее лфх, то система устойчива.
Критерий Найквиста-Михайлова: замкнутая фазовая система устойчива, если при достижении фазовой характеристикой значения –П, лах отрицательна. Частота, при которой лфх пересекает ось абсцисс называется точкой среза. В случае, если u(w) имеет несколько точек пересечения с осью абсцисс (-П), система устойчива, если число этих пересечений до частоты среза четно.
Билет 21.
При проектировании САУ обязательно требуется задавать запас устойчивости, так как:
1. Проектирование производится с учетом законов механики с отбрасыванием второстепенных факторов;
2. Все параметры рассчитываются с погрешностью;
3. Уравнения звеньев линеаризуются;
4. Расчет ведется по типовым схемам.
По критерию Михайлова на границе устойчивости задать запас в виде окружности конечного радиуса с центром в (0, 0).
По критерию Найквиста (-1, i0)…
Билет 22.
Использование критериев устойчивости для конкретной системы дает результат (один и тот же). Однако критерии имеют свои особенности.
1. Критерий Михайлова-Найквиста удобно использовать в случае возможности экспериментального определения фазовых характеристик системы. Однако вычисление АФЧХ сложнее, чем кривой Михайлова. Кроме того, требуется для ответа на вопрос об устойчивости системы также исследовать разомкнутую систему.
2. Критерий Михайлова возможно использовать для систем произвольного порядка. Совместное применение критериев Михайлова и Найквиста дает возможность постепенного построения кривых с учетом влияния каждого звена. Критерий наглядный и позволяет решать задачу выбора параметров звеньев из условий устойчивости.
3. Алгебраические критерии удобно использовать для систем малого порядка, кроме того, они не дают возможности выбора параметров системы.
Билет 23.
Анализ качества процессов управления и регулирования выполняется с использованием следующих динамических показателей:
· ty – время установления, в течение которого выходная величина достигает своего максимального значения;
· tз – время запаздывания, в течение которого выходная величина изменяется от 0 до ty/2.
· tn – длительность переходного процесса, время, за которое переходный процесс попадает в трубку радиуса E.
· tн – время нарастания, за которое выходная величина изменяется от 10% до 90% ty.
· б – перерегулирование, максимальное отклонение величины от её установившегося значения к этому установившемуся значению.
tn и б – граничные характеристики процесса.
Билет 24.
Получить кривую переходного процесса можно переходом в пространство изображений и решением дифференциального уравнения 
, которые описывают процесс.
В операторной форме: 
. Изображение исходного решения: 
, где: f(p) – изображение заданного возмущения; C0(p) – многочлен, отображающий начальные условия; G(p), F(p) – многочлены исходного уравнения.
C0(p) определяется по рекуррентным формулам. Если многочлен F(p) не имеет кратных и нулевых корней, то решение д.у. имеет вид:
, t>=0, pk – корни характеристического уравнения.
Если есть нулевой корень, то:
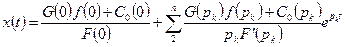
Наверное можно указать ещё методы непосредственного интегрирования и математического моделирования…
Билет 25.
Не всегда рационально использовать прямые методы оценки качества процесса управления (в случае систем порядка выше 2). В этом случае прибегают к косвенным оценкам. Для этого:
· Замена косвенного уравнения приближенным за счет отбрасывания слагаемых левой части, которые при расчетных частотах имеет малое значение. Также замена функции внешнего воздействия на более простую.
· Оценка качества процесса по распределению нулей и полюсов передаточной функции с использованием нормированных диаграмм.
· Использование интегральных оценок и методов стандартных коэффициентов при приближении исследуемого процесса к эталонному.
· Оценка качества процесса по виду вещественной частотной характеристики.
Наиболее удобной формой аппроксимации передаточной функции приближенно является её представление в логарифмическом масштабе.
Внешние возмущения аппроксимирую экспоненциальными или степенными рядами.
Используют сведение неоднородной модели к однородной.
Билет 26.
Степень устойчивости h – расстояние до ближайшего к мнимой оси корня характеристического уравнения. Если корень комплексный – степень устойчивости колебательная, если вещественный – апериодическая. h характеризует степень затухания, чем больше, тем процесс затухает быстрее.
Если ближайшие к мнимой оси корни комплексные, то угол, проходящий через эти корни и начало координат, и охватывающий остальные корни характеризует колебательность процесса. 
- степень колебательности.
Эти оценки – косвенные, показывают степень устойчивости и колебательности только косвенно, так как на эти показатели существенное влияние оказывает кратность корней.
Наиболее общим методом является отыскание корней смещенного уравнения. Вводится замена: z=p+u, x=z-u.
.
В этом случае (если u=h) смещенное уравнение будет иметь корень на мнимой оси, применяя любой из критериев (Гурвица, н-р), можно определить h (как минимальное вещественное или комплексное решение следующих уравнений) 
Формула Виета:
Система устойчива, когда вещественные части корней pi отрицательны, сл-но ai > 0. Данное условие необходимо, но не достаточно для систем порядка большего 2.
Критерий Вышнеградского для систем III порядка:
Для устойчивости системы необходимо и достаточно, чтобы выполнялись условия:
1. ai > 0
2. a2a1 > a0a3
Запишем уравнение в безразмерном виде:
p3+A2p2+A1p+1=0
Критерий Вышнеградского:
для устойчивости системы необходимо и достаточно: A1 > 0, A2 > 0, A1A2 > 1
· 3 вещественных корня (A) – апериодический процесс;
· Область (Б) – монотонный процесс, колебательная часть затухает быстрее;
· Область (В) – колебательный процесс, колебательная часть затухает медленнее.
C – точка равенства всех корней. Границе между любыми областями будет соответствовать предельное между двумя распределениями расположение корней.
Билет 27.
Интегральные оценки дают общую информацию о быстроте затухания и величине отклонения регулируемой величины.
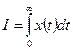, где x(t)=xпер – xоп – отклонение регулируемой величины от нового установившегося значения. В устойчивой системе при xà0, tà∞ интеграл имеет конечную величину. Геометрический смысл – площадь под кривой переходного процесса, записанного в отклонениях.
Не всегда объективен (площади могут быть отрицательными), поэтому зачастую применяют другую оценку: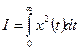 
При управлении желательно минимизировать эти оценки, однако иногда требуется поправка на скорость (не должна быть большой):
Билет 28.
На практике требуется определять характеристики системы при отклонении параметров системы от расчетных. Для оценки этого явления используют функции чувствительности:
, αj – изменяемый параметр, 0 – функция вычисляется при расчетном αj.
Исходная функция – функция, все параметры которой соответствуют расчетным (не имеют вариаций), н-р:
.
Варьируемая система – есть вариации параметров:
Дополнительное движение: 
.
При условии дифференцируемости функций по αi, возможно разложить дополнительное движение в ряд Тейлора. Для первого приближения получим следующее:
.
При существенной нелинейности используется второе приближение в ряду Тейлора.
Дифференцирование исходных уравнений ведет к получению уравнений чувствительности, решение которых позволяет найти ui,j:
Удобно использовать передаточные функции:
Функция чувствительности передаточной функции:
Билет 29.
Системы с запаздыванием – системы, имеющие в одном или нескольких звеньях запаздывание во времени начала изменения выходной величины после изменения входной на величину τ.
Уравнение динамики звена с запаздыванием можно разбить на 2:
1. Q(p)x2=R(p)x1*
2. x1*(t)=x1(t-τ)
Реальное звено с запаздыванием можно приближенно описать, используя разложение в ряд:
, p – оператор дифференцирования.
W(p)=e-τp – передаточная функция звена чистого дифференцирования.
Тогда:
Q(p)x2 = R(p) e-τp x1.
Частотная передаточная функция с запаздыванием:
W(iw)=W0(iw)e-iwτ = A0(w)ei(u(w)-τw).
