сследование свойств регрессионной модели

2.6.1. Проверка значимости коэффициентов регрессии проводится независимо друг от друга на основании t –критерия Стьюдента (Приложение Б):

, (2.7)

где s_bj — оценка среднего квадратичного отклонения погрешности определения коэффициента.

Оценка дисперсии коэффициентов, найденных по экспериментальным данным вычисляется в соответствии с выражением

. (2.8)

Оценкой генеральной дисперсии воспроизводимости s ² _воспр, характеризующая точность одного измерения, является средняя из всех построчных дисперсий

. (2.9)

При выбранном уровне статистической значимости a и при числе степеней свободы γ = N (m –1) находят табличное значение коэффициента t_табл. Найденное табличное значение сравнивается с расчетным значением коэффициента. Если выполняется неравенство t_табл > t_расч, то принимается нуль- гипотеза, т.е. считается, что найденный коэффициент b_j является статистически незначительным и его следует исключить из уравнения регрессии.

Оценка среднего квадратичного отклонения погрешности определения коэффициента s_bj при достаточном числе степеней свободы может быть определена и через остаточную дисперсию:

, j =0, n; Сjj является диагональным коэффициентом корреляционной матрицы факторов и равен , а , — значение отклика, вычисленное по построенному уравнению регрессии и называется теоретическим значением отклика при заданном наборе факторов.

2.6.2. Проверка адекватности регрессионной модели. Математическая модель должна достаточно верно качественно и количественно описывать свойства объекта исследования. Для проверки адекватности оценивают отклонение предсказанного уравнением регрессии значения выходного параметра от результатов эксперимента y_i. Для этого вычисляют дисперсию адекватности или остаточную дисперсию:

, (2.10)

где — число значимых коэффициентов модели, , причем коэффициент b ₀ в расчет не берется.

Если s ² _ост не превышает дисперсии опыта s ² _y, то полученная ММ адекватно представляет результаты эксперимента, иначе — описание считается неадекватным объекту. Проверка гипотезы об адекватности проводится с помощью F -критерия Фишера (Приложение А).

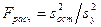. (2.11)

По уровню значимости α и степеням свободы γ ₁= N - и γ ₂= N (m -1) определяется критическое значение F (α, γ ₁, γ ₂). Если , то уравнение регрессии считается адекватным.

В случае если , то и неравенство будет выполняться всегда.

Как правило, вначале проверяют адекватность линейной ММ. Если предположение об адекватности подтверждается, то в качестве окончательной ММ выбирают линейную; если отклоняется — добавляют эффект взаимодействия с наибольшим коэффициентом и вновь проверяют гипотезу, и так до тех пор, пока существуют степени свободы.

Если в результате модель все же оказалась неадекватной, это говорит о том, что тип математической модели выбран неудачно и при данном шумовом уровне и классе точности измерительных приборов ММ должна быть уточнена. Для этого следует использовать более сложные модели, например, квадратичные (ортогональное и рототабельное композиционное планирование).