1.Построить математическую модель линейного программирования для транспортной задачи и двойственную к ней.
2.Найти начальное решение Х0 методом минимальной стоимости или методом Северо-западного угла.
3.Проверить решение на вырожденность с помощью необходимого условия.
N=m+n-1,
где m – число поставщиков, n – число потребителей, а N – число заполненных клеток.
Если число заполненных клеток (ненулевых компонент плана Х0 системы ограничений) равно m+n-1, то в этом случае решение называется невырожденным, а если число ненулевых решений не равно m+n-1, то такое решение называется вырожденным (вводится значимый нуль 
в клетку с минимальным значением Cij из оставшихся так, чтобы можно было найти потенциалы (U,V).
4.Проверка плана на оптимальность.
4.1. Вычислить потенциалы.
Потенциалы находят из решения системы:
Cij = Ui+Vj,
U1=0,
где Ui, Vj – потенциалы, переменные двойственной задачи
Cij – стоимость перевозки единицы груза
4.2. Вычисление оценок свободных клеток: 
если все оценки 
, то это признак единственного оптимального решения;
- если среди оценок имеется оценка
то это признак альтернативного оптимума, и выполняется еще один шаг для его нахождения: принять этот элемент за разрешающий. - если имеются оценки
то это признак того, что найденное решение не является оптимальным и его можно улучшить. Необходимо перейти к новому опорному решению, при этом надо перераспределить грузы, перемещая их из занятых клеток в свободные. При этом свободная клетка становится занятой, а одна из ранее занятых клеток свободной.
5. Построить новый план
5.1.Начиная с разрешающего элемента, строим замкнутый цикл, вершинами которого будут цифры плана, отличные от нуля.
Цикл может быть представлен следующими фигурами:
 | |||||||||
 |  | |  | ||||||
5.2.Помечаем вершины цикла знаками «+» и «−» поочередно, начиная с разрешающего элемента.
5.3.Находим величину сдвига по циклу - минимальный из элементов цикла, помеченных знаком «−»:
Θ= min {xij}-, xij € Z, где Z - цикл
5.4.Строим новый план х1, добавляя или вычитая, в соответствии со знаками, величину Θ к элементам цикла. И переходим на пункт 4.
6. Решить задачу в среде Microsoft Exсel, приложить отчет.
Пример решения транспортной задачи методом потенциалов
Имеется 4 оптовых склада 
с запасами однородного груза 
41; 
33; 
25;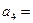 
14. Имеются 5 магазинов 
с заказами на однородный груз 
соответственно. Обозначим хij-количество груза, перевозимого со склада А1 в магазин bj. Матрица перевозок задана в следующем виде:
Таблица 2.1 – Исходные данные
| 
| 
| 
| 
| 
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
|
Условия разрешимости:
-задача закрытая
1. Математическая модель прямой ТЗ:
 | |||
 |
|
|
Двойственная задача составляется для следующих переменных:
U – переменные для складов или поставщиков;
V - переменные для магазинов или потребителей.
Математическая модель двойственной ТЗ:
Ограничения представлены на другой странице.
2.Нахождение начального решения методом Северо-Западного угла
|
|
|
|
|
| |
|
|
|
| ||||
|
|
|
| ||||
|
|
|
| ||||
|
|
|
|
Таблица 2.3 – Нахождение начального решения методом минимальной стоимости
|
|
|
|
|
|
| |
|
|
|
| ||||
|
|
| |||||
|
|
|
|
| |||
|
|
|
Значение целевой функции L(x0) при начальном решении по методу минимальной стоимости меньше, чем по методу северо-западного угла, поэтому примем его за начальное решение.
2. Проверка решения х0 на вырожденность
Количество ненулевых элементов в решении х0 равно 8, проверим условие N= m + n -1= 4 + 5 - 1=8, т.е. решение х0 не является вырожденным.
= 
Таблица 2.4. Проверка плана х0 на оптимальность.
|
|
|
|
|
|
| Ui | |
|
| 12
|
| |||||
|
|
|
| -2 | ||||
|
|
|
|
| ||||
|
|
| -1 | |||||
| Vj |
План х0 не является оптимальным, т.к. есть два положительных решения 
и 
.
. Начиная с разрешающего элемента в клетке (34), строим замкнутый цикл, вершинами которого будут цифры плана, отличные от нуля. Помечаем вершины цикла знаками «+» и «−» поочередно, начиная с разрешающего элемента. Находим величину сдвига по циклу - минимальный из элементов цикла, помеченных знаком «−».
X34 – разрешающий элемент 0*. Минимальная поставка для отрицательных вершин
θ1=min 8,14 =8.
. Организуем следующий цикл:
- 14? + 6 8
Таблица 2.5 – Проверка плана х' на оптимальность
|
|
|
|
|
|
| Ui | |
|
| 12
|
| |||||
|
|
| -2 | |||||
|
|
|
|
|
| |||
|
|
| -1 | |||||
| Vj |
план не оптимальный.
– разрешающий элемент 0*. Минимальная поставка для отрицательных вершин
Θ2=min 31,6 = 6.
Организуем второй цикл:
3 6 9 0
Строим новый план х2,
Таблица 2.6 – Проверка плана х2 на оптимальность
|
|
|
|
|
|
| Ui | |
|
| 12
|
|
| ||||
|
|
| ||||||
|
|
|
|
| ||||
|
|
| -1 | |||||
| Vj | -2 |
Все 
Оптимум достигнут
ед.
План 
оптимален, но 
– это признак альтернативного оптимума, х41 – разрешающий элемент, находим альтернативные решения х3.
|
|
? 14 14 0
ед.
Ответ: 
ед., ,
4. Решить транспортную задачу в среде Excel
В ячейках А1-Е5 вводим тарифы:
В ячейках G1-5 задаем запасы, а в ячейках А6-Е6 – заказы:
Теперь задаем область поиска решения, размер которой должен совпадать с размерностью исходной задачи. В качестве начальных значений вводим единицы:
Отдельно задаем ячейку целевой функции, используя встроенную функцию СУММ ПРОИЗВ:
В ячейках F9-12 задаем суммы по строкам, а в ячейках А13-Е13 – по столбцам:
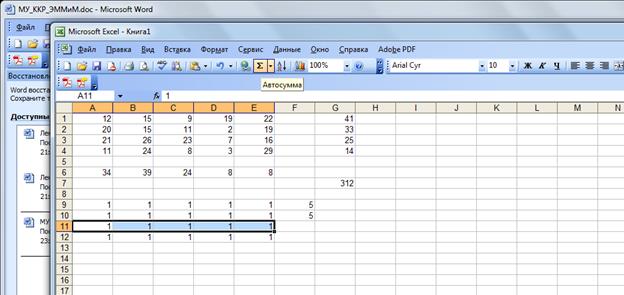
В окне Поиска решения в Параметрах выбираем метод сопряженных градиентов:
Задаем ограничения и изменяемые ячейки:
Получим решение:
ешение матричных игр
лгоритм решения
1.Проверить, имеет ли игра решение в чистых стратегиях
1.1. Найти целевую функцию первого игрока V1. Из всех чисел по строкам выбираем минимальные, а затем среди них выбираем максимальное значение:
V1=α = max min hij
i j
1.2. Найти целевую функцию второго игрока. Из всех чисел столбцов выбираем максимальные значения, а затем из них выбираем минимальное значение:
V2=β = min max hij
j i
1.3. Если α = β, то игра имеет решение в чистых стратегиях.
Если α ≠ β, то игра решается в смешанных стратегиях.
2. Решение игры в смешанных стратегиях:
2. 1. Упростить игру с помощью правил доминирования.
Упрощение состоит в том, что в матрице выигрышей H вычеркиваются минимальные строки и максимальные столбцы. При упрощении игры не учитываются элементы в вычеркнутых стратегиях.
2. 2. Если после упрощения получили игру размерности [2 х 2], то находим решение аналитически с помощью формул. Если получили игры размерности [2 х n] или [m х 2], то с помощью геометрического доминирования эти игры свести к игре размерности [2 х 2] и решить аналитически.
2.3. Если после упрощения игра осталась размерности [m x n], то найти ее решение сведением к задачам линейного программирования.
2.4. Исходную игру свести к задачам линейного программирования и решить с помощью программы Simplex Solver и приложить отчет.
2.2 Примеры решения матричных игр размерности [2х2], [2хn], [mx2]
1) Решение игр размерности [2x2]
Х*
У* 
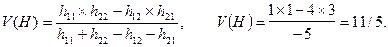
Х*
У* 
Проверка:
= 
Ответ: 
2) Решение игр размерности [mx2]
Целевая функция игроки 2:V2=min max HiYT, i=1,2,…,m.
yєS1 i
| αi = min hij j | V2 = max αii i |
| -1 | |
| βj = max hij i | ||
| V1 = min βii j |
Рис. 1. Геометрическая интерпретация исходной игры
С помощью геометрического доминирования исходная игра сведена к игре размерности [2х2]
, 
, 
.
Проверка:
X*HY*T = 
Ответ: 
3) Решение игр размерности [2xn]
Целевая функция игрока 1: V1=max min XHj, j=1,2,…,n.
xєS 1 j
| αi = min hij j | V1 = max αii i |
| 0.4 | 0.5 |
| 0.5 |
| βj = max hij i | 0.9 | ||
| V2 = min βii j | 0.9 |
Рис. 2. Геометрическая интерпретация исходной игры
С помощью геометрического доминирования исходная игра свелась к игре размерности [2х2]
; 
;
.
X*
Y* 5/11 0 6/11
Проверка:
Ответ: 
