19.1 Лемма о непрерывности произвольного иногочлена. Функция f(x) называется непрерывной, если она непрерывна во всех точках х0, в которых она определена. Многочлен f(x) определен во всей комплексной плоскости. Докажем, что многочлен, как функция, непрерывен во всей комплексной плоскости.
Если свободный член многочлена f(x) равен нулю, f(x)=a0xn+a1xn-1+...+an-1x, т.е. f(0)=0, то для всякого e>0 можно подобрать такое d>0, что при всех х, для которых |х|<d, будет |f(x)|< e. Доказательство. Пусть A=max{ |a0|,|a1|,...,|an-1|}, число e - задано. В качестве d возьмем число 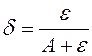 и покажем, что это число удовлетворяет требуемым условиям. В самом деле: |f(x)|£|a0||x|n+|a1|x|n-1+...+|an-1|x|£A(|x|n+|x|n-1+...+|x|) или |f(x)|£
и покажем, что это число удовлетворяет требуемым условиям. В самом деле: |f(x)|£|a0||x|n+|a1|x|n-1+...+|an-1|x|£A(|x|n+|x|n-1+...+|x|) или |f(x)|£ 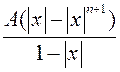 , т.к. справа сумма убывающей геометрической прогрессии, рассмотрение ведется вблизи |х|=0. В связи с тем, что |х|< d, a
, т.к. справа сумма убывающей геометрической прогрессии, рассмотрение ведется вблизи |х|=0. В связи с тем, что |х|< d, a 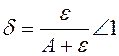 , то
, то 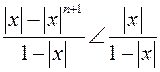 и поэтому
и поэтому 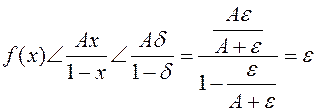 Или, подбираем d так, чтобы
Или, подбираем d так, чтобы 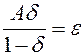 отсюда
отсюда 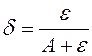 <1
<1
19.2 Формула Тейлора. Пусть дан многочлен f(x)=a0xn+a1xn-1+...+an с любыми числовыми коэффициентами. Подставим в него вместо х сумму х+h, где h – второе неизвестное. Получим: f(x+h)=a0(x+h)n+a1(x+h)n-1+...+anСтепени (x+h)k, k£n можно разложить по биному Ньютона, собрать подобные члены и получить формулу: 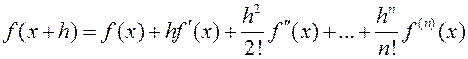 Это и есть формула Тейлора.
Это и есть формула Тейлора.
19.3 Теоеме о непрерывности произвольного многочлена. Произвольный многочлен f(x) с комплексными коэффициентами непрерывен в любой точке х0 комплексной плоскости. По формуле Тейлора 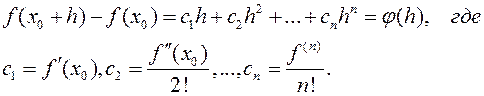 j(h) - многочлен без свободного члена. По лемме 1. для всякого e>0 можно подобрать d>0, такое, что при |h|< d будет |f (h)|< e, т.е. |f(x0+h)-f(x0)|< e. Пусть дан многочлен f(x) с комплексными коэффициентами, тогда его модуль |f(x)| можно рассматривать как действительную неотрицательную функцию комплексного переменного. По свойствам модулей комплексных чисел
j(h) - многочлен без свободного члена. По лемме 1. для всякого e>0 можно подобрать d>0, такое, что при |h|< d будет |f (h)|< e, т.е. |f(x0+h)-f(x0)|< e. Пусть дан многочлен f(x) с комплексными коэффициентами, тогда его модуль |f(x)| можно рассматривать как действительную неотрицательную функцию комплексного переменного. По свойствам модулей комплексных чисел 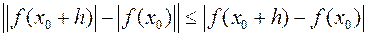 , а, учитывая доказанную теорему, это означает непрерывность модуля многочлена с комплексными коэффициентами и комплексным переменным.
, а, учитывая доказанную теорему, это означает непрерывность модуля многочлена с комплексными коэффициентами и комплексным переменным.
19.4.Лемма о модуле старшего члена. Пусть дан многочлен f(x)=a0xn+a1xn-1+...+an степени n³1 с произвольными комплексными коэффициентами.Если k - любое положительное число, то для достаточно больших по модулю значений неизвестного х имеет место неравенство: 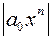 >
> 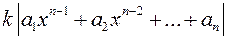 , (*) т.е. модуль старшего члена больше модуля всех остальных членов во сколько угодно раз. Доказательство. Пусть А=max{|a1|,|a2|,...,|an|}. Тогда по свойству модулей комплексных чисел
, (*) т.е. модуль старшего члена больше модуля всех остальных членов во сколько угодно раз. Доказательство. Пусть А=max{|a1|,|a2|,...,|an|}. Тогда по свойству модулей комплексных чисел 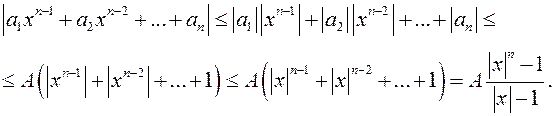 Если |х|>1, то
Если |х|>1, то 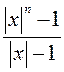 <
< 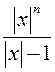 , откуда
, откуда 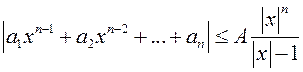 , Выберем х таk, чтобы выполнялись условия: |х|>1 и х >
, Выберем х таk, чтобы выполнялись условия: |х|>1 и х > 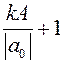 , тогда
, тогда 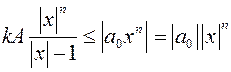 В этом случае выполняется и неравенство (*).
В этом случае выполняется и неравенство (*).
19.5 Лемма о возрастании модуля многочлена. Для всякого многочлена f(x) с комплексными коэффициентами, степень которого не меньше 1, и всякого действительного положительного числа М, сколь угодно большого, можно подобрать такое действительное положительное число N, что при |х|>N |f(x)|>M. Пусть f(x)=a0xn+a1xn-1+...+an. По свойствам модулей комплексных чисел |f(x)|=|a0xn+(a1xn-1+...+an)|³|a0xn|- |a1xn-1+...+an| (*) Применим лемму о модуле старшего члена, положив k=2: |a0xn|>2|a1xn-1+...+an| при некотором |х|>N1, отсюда |a1xn-1+...+an|<1/2|a0xn|, подставим это в (*), получим: |f(x)|>|a0xn|-1/2|a0xn|=1/2|a0xn|. Правая часть этого неравенства будет больше нашего числа М, если 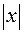 >
> 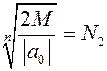 . Таким образом, |х|>N={maxN1,N2} будем иметь |f(x)|>M.
. Таким образом, |х|>N={maxN1,N2} будем иметь |f(x)|>M.
19.6Лемма Даламбера. Если при х=х0 многочлен f(x) степени n³1 не обращается в 0, то можно найти такое приращение h, в общем случае комплексное, что |f(x0+h)|<|f(x0)|. Вспомним формулу Тейлора: 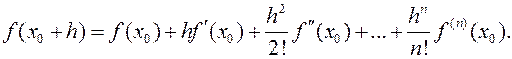 По условию х0 не является корнем для f(x), но случайно может оказаться корнем для f'(x) или для других производных. Пусть k-тая производная (k³1) - первая, для которой х0 не является корнем, т.е. f'(x0)=f''(x0)=...=f(k-1)(x0)=0, f(k)(x0)¹0. Такая производная существует, т.к. по крайней мере f(n)(x0)=a0n!¹0. Тогда:
По условию х0 не является корнем для f(x), но случайно может оказаться корнем для f'(x) или для других производных. Пусть k-тая производная (k³1) - первая, для которой х0 не является корнем, т.е. f'(x0)=f''(x0)=...=f(k-1)(x0)=0, f(k)(x0)¹0. Такая производная существует, т.к. по крайней мере f(n)(x0)=a0n!¹0. Тогда: 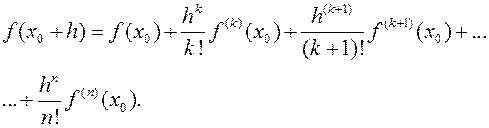 Делим обе части этого равенства на f(x0) (ведь f(x0)¹0).
Делим обе части этого равенства на f(x0) (ведь f(x0)¹0).
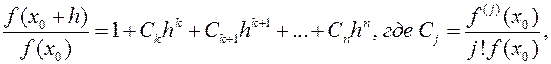 при этом, т.к. f(k)(x0)¹0, то и Ck¹0, значит,
при этом, т.к. f(k)(x0)¹0, то и Ck¹0, значит, 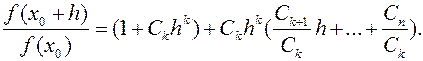 Теперь перейдем к модулям:
Теперь перейдем к модулям: 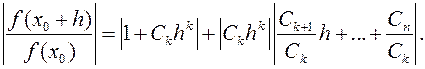 До этого мы не делали предположения о величине h. Выберем для h отдельно его модуль и его аргумент. а) Модуль выберем так, чтобы многочлен без свободного члена удовлетворял неравенству:
До этого мы не делали предположения о величине h. Выберем для h отдельно его модуль и его аргумент. а) Модуль выберем так, чтобы многочлен без свободного члена удовлетворял неравенству: 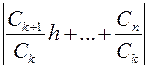 <
<  при некотором |h|< d1. (По лемме о многочлене без свободного члена это возможно). Сkhk - тоже многочлен без свободного члена, поэтому его модуль может быть |Сkhk|<1 при |h|< d2<
при некотором |h|< d1. (По лемме о многочлене без свободного члена это возможно). Сkhk - тоже многочлен без свободного члена, поэтому его модуль может быть |Сkhk|<1 при |h|< d2< 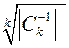 (*) Теперь модуль |h| выберем так, чтобы |h|<min { d1, d2}, тогда
(*) Теперь модуль |h| выберем так, чтобы |h|<min { d1, d2}, тогда 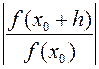 <
< 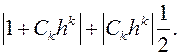 Условием (*) воспользуемся потом. б) Аргумент h выберем так, чтобы Сkhk было бы отрицательным действительным числом, т.е., чтобы arg (Ckhk)=arg Ck+karg h=p, откуда arg h=
Условием (*) воспользуемся потом. б) Аргумент h выберем так, чтобы Сkhk было бы отрицательным действительным числом, т.е., чтобы arg (Ckhk)=arg Ck+karg h=p, откуда arg h=  . При таком выборе h число Сkhk, будет отличаться от своего модуля только знаком: Ckhk=-|Ckhk|. Теперь используем условие (*), тогда 1+Ckhk=1-|Ckhk| или |1+Ckhk|=|1-|Ckhk||=1-|Ckhk|. Таким образом, выбирая h по модулю и аргументу, получим:
. При таком выборе h число Сkhk, будет отличаться от своего модуля только знаком: Ckhk=-|Ckhk|. Теперь используем условие (*), тогда 1+Ckhk=1-|Ckhk| или |1+Ckhk|=|1-|Ckhk||=1-|Ckhk|. Таким образом, выбирая h по модулю и аргументу, получим: 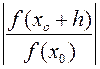 <
< 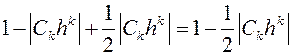 <1, т.е.
<1, т.е. 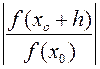 =<
=<  <1. Вообразим себе пространственную поверхность функции |f(x)| над комплексной плоскостью: если при некотором х0 |f(x0)|>0, то найдется такое h, что при х0+h значение функции будет ближе к нулю, т.е. функция убывающая (как уже говорилось |f(x)| - это действительная функция комплексного переменного). Таким образом, у функции |f(x)| отсутствуют локальные экстремумы, если f(x)¹0. Капля воды, опущенная на поверхность |f(x)| над комплексной плоскостью, обязательно скатится до той точки поверхности, которая соприкасается с комплексной плоскостью, т.е. до нуля.
<1. Вообразим себе пространственную поверхность функции |f(x)| над комплексной плоскостью: если при некотором х0 |f(x0)|>0, то найдется такое h, что при х0+h значение функции будет ближе к нулю, т.е. функция убывающая (как уже говорилось |f(x)| - это действительная функция комплексного переменного). Таким образом, у функции |f(x)| отсутствуют локальные экстремумы, если f(x)¹0. Капля воды, опущенная на поверхность |f(x)| над комплексной плоскостью, обязательно скатится до той точки поверхности, которая соприкасается с комплексной плоскостью, т.е. до нуля.
19.7 Формулировка теоремы Вейерштрасса. Если действительная функция g(x) комплексного переменного х непрерывна во всех точках замкнутого круга Е, то в круге Е существует такая точка х0, что для всех х из Е имеет место неравенство g(x0)£g(x).Т.е. точка х0 является точкой минимума для g(x) в круге Е. (g(x)=|f(x)|).
19.8 Доказательство основной теоремы алгебры. Всякий многочлен с любыми числовыми коэффициентами, степень которого не меньше единицы, имеет хотя бы один корень, в общем случае комплексный. Доказательство основной теоремы. Дан многочлен f(x) степени n³. Полагаем, что его свободный член аn ¹0. Если аn=0, то х=0 – корень этого многочлена, для этого случая теорема верна. Очевидно, что f(0)=an. 1.Применим лемму о возрастании модуля многочлена, полагая, что М=|аn|. Т.е. существует такое число N, что при |x|>N |f(x)|>|f(0)|=|an|. 2.Теперь применим к этому многочлену теорему Веерштрасса. В качестве Е возьмем круг радиуса N с центром в точке 0. Вне этого круга (|х|>N) |f(x)|>|f(0)|=|an|, значит, внутри этого круга найдется точка х0, такая, что |f(x0)|£|f(x)| и, в том числе, |f(x0)| £|f(0)|. Пусть точка х0 будет точкой минимума для |f(x)| в круге Е. Отсюда следует, что: а) х0 будет точкой минимума для |f(x)| на всей комплексной плоскости, т.к. вне круга |f(x)|>|f(0)| ³|f(x0)| (при |х|>N). б) f(x0)=0, т.е. х0 служит корнем для f(x). Если бы f(x0) ¹0, то
по лемме Даламбера существовала бы точка х1, такая, что |f(x1)|<|f(x0)|, но тогда х0 - не точка минимума, это противоречие.
1.9 Следствия из основной теоремы алгебры. 1.Любой многочлен f(x)=a0xn+a1xn-1+...+an степени n³1 (*) с любыми комплексными коэффициентами разлагается в произведение n линейных множителей: f(x)=a0(x-a1)(x-a2)...(x-an). (**) Доказательство: По основной теореме у f(x) есть корень a1, комплексный или действительный, тогда f(x)=(x-a1)g1(x). Коэффициенты многочлена g1(x) снова комплексные или действительные, поэтому g1(x) обладает корнем a2, причем, a2 - корень и для f(x), т.к. f(x)=(x-a1)[(x-a2)g2(x)], и т.д. тf(x)=a0(x-a1)(x-a2)...(x-an). Коэффициент а0 появился потому, что после умножения в правой части коэффициенты при старшем и других членах (по степеням х) должны быть одинаковыми с соответствующими коэффициентами в левой части. 2.Разложение (**) является для многочлена f(x) единственным с точностью до порядка следования сомножителей. Пусть имеется еще одно разложение такого типа: f(x)=a0(x-b1)(x-b2)...(x-bn), т.е. (x-a1)(x-a2)...(x-an)= (x-b1)(x-b2)...(x-bn). Если бы корень ai был отличен от всех корней bi, то, подставляя ai в обе части равенства вместо х, мы получили бы слева 0, а справа число, отличное от 0. Значит, среди b есть корень, равный ai. Т.е. всякий ai равен некоторому корню bj и наоборот. Отсюда еще не следует совпадение разложений, т.к. среди корней ai могут быть равные между собой. Пусть в разложении слева ai содержится s раз и пусть справа среди bj содержится t корней, равных корню ai. Покажем, что s=t. Отступление. а)Произведение двух многочленов не может равняться 0, если они оба отличны от 0, т.к. степень произведения равна сумме степеней сомножителей. б)Если два произведения равны друг другу, то их можно сократить на общий множитель: пусть (x)h(x)=g(x)h(x), h(x)¹0, тогда [f(x)-g(x)]h(x)=0 ® f(x)-g(x)=0 ® f(x)=g(x). Применяя эти рассуждения к нашим разложениям, получим: если s>t, то сократим наше равенство на (x-ai)t, получим, что левая часть еще содержит множитель х-ai, а правая - нет -это противоречие. Объединяя одинаковые множители разложения, получим: f(x)= 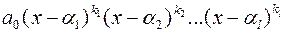 , где k1+k2+...+kl=n, при этом ai¹aj при i ¹ j, i,j=1,2,...l. 3.Мы доказали: Всякий многочлен f(x) степени n³1 с любыми числовыми коэффициентами имеет n корней, если каждый из корней считать столько раз, какова его кратность. Это справедливо даже для многочлена нулевой степени (числа), у него 0 корней, но неприемлемо для многочлена - нуля, не имеющего степени и равному 0 при любых х (¥-число корней).
, где k1+k2+...+kl=n, при этом ai¹aj при i ¹ j, i,j=1,2,...l. 3.Мы доказали: Всякий многочлен f(x) степени n³1 с любыми числовыми коэффициентами имеет n корней, если каждый из корней считать столько раз, какова его кратность. Это справедливо даже для многочлена нулевой степени (числа), у него 0 корней, но неприемлемо для многочлена - нуля, не имеющего степени и равному 0 при любых х (¥-число корней).
19.10 Формулы Вьета. Дан многочлен f(x) степени n, со старшим коэффициентом, равным 1: f(x)=xn+a1xn-1+a2xn-2+...+an-1x+an. пусть a1,a2,…,an - его корни. Тогда его разложение будет: f(x)=(x-a1)(x-a2)...(x-an)= xn+a1xn-1+a2xn-2+...+an-1x+an.Перемножая скобки, приводя подобные члены и сравнивая коэффициенты при одинаковых степенях х, получим выражение коэффициентов через корни. Это и есть формулы Вьета:
a1=-(a1+a2+…+an);
a2=a1a2+a1a3+…+a1an+a2a3+…+an-1an;
a3=-(a1a2a3+a1a2a4+…+an-2an-1an);
...................................................
an-1=(-1)n-1(a1a2…an-1+a1a2…an-2an+…+a1a2…an);
an=(-1)n(a1a2…an). Таким образом, в правой части k-го равенства (k=1,2,...,n) стоит сумма всевозможных произведений по k корней, умноженная на (-1)k, т.е. взятая со знаком "+" или "-" в зависимости от четности k.Если старший коэффициент а0¹0, то все коэффициенты нужно разделить на а0 (что не влияет на корни).
19.11 Свойство многочлена с действительными коэффициентами. Пусть многочлен с действительными коэффициентами f(x)=a0xn+a1xn-1+...+an имеет комплексный корень a, т.е. f(a)=a0an+a1an-1+...+an=0 Равенство не нарушится, если в нем все числа заменить на комплексно-сопряженные, но т.к. коэффициенты в f(x) действительные, то на сопряженные заменяются только степени a, значит 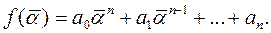 1.Если комплексное число a служит корнем многочлена f(x) с действительными коэффициентами, то сопряженное число
1.Если комплексное число a служит корнем многочлена f(x) с действительными коэффициентами, то сопряженное число 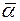 будет корнем для f(x). 2.Многочлен f(x) будет делиться на квадратный трехчлен j(x)=(x-
будет корнем для f(x). 2.Многочлен f(x) будет делиться на квадратный трехчлен j(x)=(x- 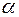 )(x-
)(x- 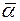 )=x2-(
)=x2-(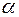 +
+ 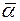 )x+
)x+ 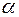
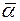 , Коэффициенты которого - действительные числа. 3.Корни
, Коэффициенты которого - действительные числа. 3.Корни 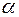 и
и 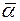 имеют в многочлене f(x) одну и ту же кратность. Пусть их кратности разные: k и p, пусть k>p. Тогда f(x) делится на p-ю степень квадратного трехчлена j(x)=
имеют в многочлене f(x) одну и ту же кратность. Пусть их кратности разные: k и p, пусть k>p. Тогда f(x) делится на p-ю степень квадратного трехчлена j(x)= 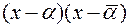 , т.е. f(x)=jp(x)q(x). q(x)- частное от деления многочленов с действительными коэффициентами и имеет коэффициенты из того же поля действительных чисел. Но в противоречие с доказанным он имеет a своим (k-p)-кратным корнем, а
, т.е. f(x)=jp(x)q(x). q(x)- частное от деления многочленов с действительными коэффициентами и имеет коэффициенты из того же поля действительных чисел. Но в противоречие с доказанным он имеет a своим (k-p)-кратным корнем, а 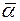 - не является его корнем, значит, k=p. 4.Из сказанного следует, что комплексные корни всякого многочлена попарно сопряжены. 5.Всякий многочлен f(x) с действительными коэффициентами представим, при том единственным способом (с точностью до порядка следования сомножителей), в виде произведения своего старшего коэффициента а0 и нескольких многочленов вида x- a, где a - действительные числа, его действительные корни, и квадратных многочленов, соответствующим парам комплексных корней. 6.Многочлен с действительными коэффициентами с нечетной степенью имеет хотя бы один действительный корень.Наглядно можно себе представить модуль многочлена как поверхность над комплексной плоскостью, кое-где точечно соприкасающуюся с плоскостью (корни). Точек касания n штук, они симметричны относительно оси х или лежат на ней. Если в разложении многочлена есть квадратный трехчлен вида x2+cx+d, то сразу можно найти его комплексные корни из условия:
- не является его корнем, значит, k=p. 4.Из сказанного следует, что комплексные корни всякого многочлена попарно сопряжены. 5.Всякий многочлен f(x) с действительными коэффициентами представим, при том единственным способом (с точностью до порядка следования сомножителей), в виде произведения своего старшего коэффициента а0 и нескольких многочленов вида x- a, где a - действительные числа, его действительные корни, и квадратных многочленов, соответствующим парам комплексных корней. 6.Многочлен с действительными коэффициентами с нечетной степенью имеет хотя бы один действительный корень.Наглядно можно себе представить модуль многочлена как поверхность над комплексной плоскостью, кое-где точечно соприкасающуюся с плоскостью (корни). Точек касания n штук, они симметричны относительно оси х или лежат на ней. Если в разложении многочлена есть квадратный трехчлен вида x2+cx+d, то сразу можно найти его комплексные корни из условия: 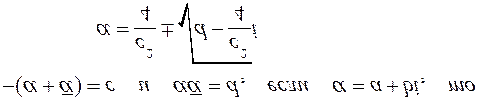 Итак, основная теорема алгебры утверждает: - существование корня многочлена; - достаточность поля комплексных чисел для существования корня; - равенство количества корней многочлена его степени (с учетом их кратностей) - это следствие из основной теоремы.
Итак, основная теорема алгебры утверждает: - существование корня многочлена; - достаточность поля комплексных чисел для существования корня; - равенство количества корней многочлена его степени (с учетом их кратностей) - это следствие из основной теоремы.
20.1Границы действительных корней многочлена. Полагая k=1, получим, что при 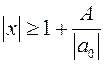 модуль старшего члена больше модуля суммы всех остальных членов и никакое значение х, удовлетворяющее этому неравенству не может быть корнем многочлена. Здесь f(x)=a0xn+a1xn-1+...+an, A=max{|a1|,|a2|...|an|}, т.е. Число
модуль старшего члена больше модуля суммы всех остальных членов и никакое значение х, удовлетворяющее этому неравенству не может быть корнем многочлена. Здесь f(x)=a0xn+a1xn-1+...+an, A=max{|a1|,|a2|...|an|}, т.е. Число 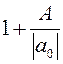 1 - верхняя, грубая граница модулей корней многочлена (всех, и комплексных и действительных). Пример. (x)=x5+2x4-5x3+8x2-7x-3, а0=1, А=8, верхняя граница- 9. Покажем, что в действительности достаточно иметь лишь верхнюю границу положительных корней многочлена. Пусть дан f(x) - многочлен степени n, N0 - верхняя граница егоположительных корней. Рассмотрим многочлены:
1 - верхняя, грубая граница модулей корней многочлена (всех, и комплексных и действительных). Пример. (x)=x5+2x4-5x3+8x2-7x-3, а0=1, А=8, верхняя граница- 9. Покажем, что в действительности достаточно иметь лишь верхнюю границу положительных корней многочлена. Пусть дан f(x) - многочлен степени n, N0 - верхняя граница егоположительных корней. Рассмотрим многочлены: 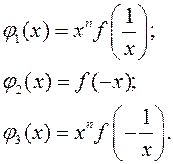 Найдем верхние границы их положительных корней, пусть это будут числа N1, N2, N3. Тогда число 1/N1 будет нижней границей положительных корней многочлена f(x).Пусть a - положительный корень f(x), тогда 1/a - положительный корень для j1(x) и из неравенства
Найдем верхние границы их положительных корней, пусть это будут числа N1, N2, N3. Тогда число 1/N1 будет нижней границей положительных корней многочлена f(x).Пусть a - положительный корень f(x), тогда 1/a - положительный корень для j1(x) и из неравенства 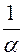 <N1 следует неравенство. a >
<N1 следует неравенство. a > 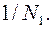 .Аналогично, числа -N2 и -1/N3 служат соответственно нижней и верхней границами отрицательных корней f(x).Таким образом, все положительные корни удовлетворяют неравенствам:
.Аналогично, числа -N2 и -1/N3 служат соответственно нижней и верхней границами отрицательных корней f(x).Таким образом, все положительные корни удовлетворяют неравенствам: 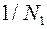 < a < N0. Все отрицательные корни удовлетворяют неравенствам: - N2 < a <
< a < N0. Все отрицательные корни удовлетворяют неравенствам: - N2 < a < 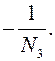
20.2 Теорема Штурма а) Перемена знаков. Пример: дана упорядоченная система чисел 1,3,-2,1,5,-6,-8,3. Выпишем знаки чисел: +,+,-,+,+,-,-,+. В последовательности знаков 4 раза рядом стоят + и -. Наша система чисел имеет 4 перемены знаков.б) Система Штурма. Пусть f(x) - многочлен с действительными коэффициентами, не имеющий кратных корней, т.е. f(x) взаимно прост со своей производной. Определение. Конечная упорядоченная система отличных от нуля многочленов с действительными коэффициентами f(x)=f0(x), f1(x), f2(x),...,fs(x) называется системой Штурма для многочлена f(x), если выполняются требования: 1) соседние многочлены не имеют общих корней; 2) последний многочлен fs(x) не имеет действительных корней; 3) если a - действительный корень одного из промежуточных многочленов fk(x) (1£ k £ s-1), то fk-1(a) и fk+1(a) имеют разные знаки; 4) если a0 - действительный корень многочлена f(x), то произведение f(x)f `(x) меняет знак с "-" на "+", когда х, возрастая, проходит через точку a. Пусть f0,f1,...fs - система Штурма многочлена f(x).
Пусть с - действительное число, не являющееся корнем многочлена f(x).
вычислим систему чисел f(c)=f0(c), f1(c),...fs(c). Вычеркнем из нее нули. Обозначим w(c) - число перемен знаков в оставшейся системе. Тогда w(c) - число перемен знаков в системе Штурма многочлена f(x) при х=с.Теорема Штурма. ЕСЛИ ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА а И b, a<b НЕ ЯВЛЯЮТСЯ КОРНЯМИ МНОГОЧЛЕНА f(x), НЕ ИМЕЮЩЕГО КРАТНЫХ КОРНЕЙ, ТО w(a) ³ w(b) И РАЗНОСТЬ w(a)-w(b) РАВНА ЧИСЛУ ДЕЙСТВИТЕЛЬНЫХ КОРНЕЙ МНОГОЧЛЕНА f(x), ЗАКЛЮЧЕННЫХ МЕЖДУ a и b Доказательство. Исходим из того, что система Штурма построена. 1.Если х, возрастая, переходит через значение корня f(x), не имеющего кратных корней, то многочлен f(x) меняет знак. Докажем это утверждение от противного. Пусть a-корень многочлена f(x) и f(x) не меняет знак при переходе х через a, т.е. f(a-e) и f(a+e) одного знака, а f(a)=0, но тогда и f'(a)=0 (см. рис.). Т.е. f(x) имеет кратные корни, a - кратный корень, что противоречит условию 2.Если х, возрастая, не встретит ни одного корня многочлена системы Штурма, то w(x) не изменится. 3.Пусть a - корень многочлена fk(x), (k=2...s-1), тогда по условию 1.
fk-1(a)¹0, fk+1(a)¹0. Следовательно, можно найти положительное число e (может быть малое), такое, что на отрезке [a-e, a+e] fk-1(x) и fk+1(x) не имеют корней и поэтому сохраняют постоянные знаки. По условию 3. эти знаки разные. Следовательно, каждая из систем чисел fk-1(a-e), fk(a-e), fk+1(a-e) и fk-1(a+e), fk(a+e), fk+1(a+e) обладает ровно одной переменой знаков, не зависимо от того, какие знаки имеют числа fk(a- e) и fk(a+e). Т.е. возможны лишь такие варианты:
- - + - + + + - - + + -
- + + - - + + + - + - - везде одна перемена знаков Вывод из этих рассуждений: При переходе х через корень одного из промежуточных многочленов системы Штурма перемены знаков в этой системе не возникают и не исчезают. Число w(x) при таком переходе не меняется. 4.Пусть a - корень многочлена f(x). По условию 1. a не будет корнем многочлена f1(x). Следовательно, существует положительное число e>0, такое, что при a-e< x<a+e - на этом отрезке нет корней у f1(x), т.е. f1(x) сохраняет свой знак на этом отрезке. Возможны ситуации:
а) f(x) f1(x) w(x) b) f(x) f1(x) w(x)
x= a-e - + 1 x=a-e + - 1
x= a 0 + 0 x=a 0 - 0
x= a+e + + 0 x=a+e - - 0 Здесь, как мы видим, f(x) меняет знак при переходе х через корень, произведение f(x)f1(x) изменяет при этом знак с "-" на "+", как этого требует 4-ое условие ряда Штурма. Это же условие отвергает две другие ситуации:
с) f(x) f1(x) d) f(x) f1(x)
x=a-e - - x=a-e + +
x=a 0 - x=a 0 +
x=a+e + - x=a+e - + Таким образом, при переходе х через корень многочлена f(x) происходит одна потеря перемен знаков в системе Штурма и происходит она на многочленах f0(x) и f1(x). Число w(x) меняется при возрастании х лишь при переходе х через корень f(x), при этом оно уменьшается ровно на единицу
20.3 Построение системы Штурма. Пусть дан многочлен f(x), не имеющий кратных корней. Тогда 1. f0(x)=f(x). 2. Пусть f1(x)=f'(x). Условие 1) выполняется, т.к. f(x) не имеет кратных корней. Докажем выполнение условия 4). Пусть a - корень f(x). a) Если f'(x)>0, то f(x) в окрестности х=a - возрастающая функция, значит f(x) меняет знак с "-" на "+" при переходе х через a, тогда произведение f(x)f'(x) будет менять знак с "-" на "+" при переходе х через a.б) Если f'(x)<0, то f(x) в окрестности х=a - убывающая функция и произведение f(x)f'(x) опять будет менять знак c "-" на "+" при переходе х через a (см. рис.). 3. Разделим f(x) на f'(x)=f41 0(x) и остаток от этого деления, взятый с обратным знаком, примем за f2(x), т.е. f(x)=f1(x)q1(x)-f2(x). И вообще, если найдены fk-1(x) и fk(x), то fk+1(x) будет остатком от деления fk-1(x) на fk(x), взятым с обратным знаком: fk-1(x)=fk(x)qk(x)-fk+1(x). (*) От алгоритма Евклида этот процесс отличается лишь переменой знака у каждого следующего остатка, что не влияет на отыскание наибольшего общего делителя (НОД). Но НОД в этом случае равен 1, т.к. f(x) и f'(x) - взаимно просты (нет общих корней у f(x)). Т.е. fs(x) будет отличным от нуля числом, выполняется условие 2. Проверим выполнение условия 1. (От противного) Пусть a - корень многочленов fk и fk+1. По равенству (*) a будет корнем и fk-1 перейдем к предыдущему равенству, a будет корнем и fk-2...f1 и f, но это противоречит условию отсутствия кратных корней у многочлена f(x). Выполнение условия 3. также вытекает из равенства (*). Если fk(a)=0, то fk-1=-fk+1.
 f(x) f(x)
f(x) f(x)

 f>0, f `<0 f>0, f `>0
f>0, f `<0 f>0, f `>0
a x a 
 x
x
f<0, f `<0 f<0, f `>0
20.4 Метод Ньютона нахождения корней многочлена. Пусть f(x) - многочлен степени n³1, не имеющий кратных корней. Пусть х0 - приближенное значение корня (например, из графика), тогда 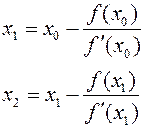 x1 - более точное значение корня, x2 - еще более точное значение и т.д. В точке х0, с которой начинается счет, знак f(x0) должен совпадать со знаком f ''(x0). Если f(x) имеет кратные корни, то их нужно вначале выделить: найти НОД f(x) и f '(x) и разделить f(x) на НОД. Это и будет многочлен без кратных корней, но все его корни совпадают с корнями f(x)
x1 - более точное значение корня, x2 - еще более точное значение и т.д. В точке х0, с которой начинается счет, знак f(x0) должен совпадать со знаком f ''(x0). Если f(x) имеет кратные корни, то их нужно вначале выделить: найти НОД f(x) и f '(x) и разделить f(x) на НОД. Это и будет многочлен без кратных корней, но все его корни совпадают с корнями f(x)
21.1 Бинарные отношения и операции. Для любых двух множеств X и Y всякое подмножество О X 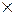 Y называется бинарным отношением между множествами X и Y. Здесь X
Y называется бинарным отношением между множествами X и Y. Здесь X 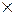 Y - декартово произведение множеств X и Y, т.е. множество всех упорядоченных пар (х,y). O - подмножество этих пар. Если Y=X, то X
Y - декартово произведение множеств X и Y, т.е. множество всех упорядоченных пар (х,y). O - подмножество этих пар. Если Y=X, то X 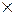 X - декартов квадрат (плоскость). Например: x<y - упорядоченная пара, половина плоскости. Бинарной алгебраической операцией на множестве X называется произвольное, но фиксированное отображение t: X
X - декартов квадрат (плоскость). Например: x<y - упорядоченная пара, половина плоскости. Бинарной алгебраической операцией на множестве X называется произвольное, но фиксированное отображение t: X 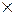 X®X, декартова квадрата X2 в X. Другими словами: Любой упорядоченной паре (a,b) элементов a,bÎX ставится в соответствие однозначно определенный третий элемент t(a,b). Примеры: 1). Z - множество целых чисел. Бинарные операции: n+m, n×m, n-m, n*m=n+m-nm, n°m=-n-m и т.д. 2). Дифференцирование - не бинарная операция, т.к.действие производится над одним элементом - функцией. 3). Отыскание детерминанта матрицы - не бинарная операция по той же причине.
X®X, декартова квадрата X2 в X. Другими словами: Любой упорядоченной паре (a,b) элементов a,bÎX ставится в соответствие однозначно определенный третий элемент t(a,b). Примеры: 1). Z - множество целых чисел. Бинарные операции: n+m, n×m, n-m, n*m=n+m-nm, n°m=-n-m и т.д. 2). Дифференцирование - не бинарная операция, т.к.действие производится над одним элементом - функцией. 3). Отыскание детерминанта матрицы - не бинарная операция по той же причине.
21.2 Полугруппа. Моноид. Множество Х с заданной на нем одной бинарной ассоциативной операцией называется полугруппой. Множество Х с заданной на нем одной бинарной ассоциативной операцией и нейтральным элементом относительно этой операции называется моноидом. (Моноид - полугруппа с единицей). Обозначение моноида: (М,*). Пример 1. nZ={nm|mÎZ} - множество целых чисел, делящихся на n.(nZ,+,0) - это коммутативный моноид относительно операции сложения. Пример 2. n>1; (nZ, ×), если n=2, это четные числа. Это полугруппа относительно операции умножения, т.к. в этом множестве нет нейтрального элемента. Пример 3. {Mn(R),+,0} - множество квадратных матриц порядка n с нулевой матрицей - это коммутативный моноид относительно операции сложения. Пример 4. {Mn(R), ×,E} - некоммутативный моноид с единичной матрицей Е.
21.3 Подполугруппы, подмоноиды. Подмножество S' полугруппы S с операцией * называется подполугруппой, если x*y принадлежит S' для всех x,y, принадлежащих S'. Или, если подмножество S' замкнуто относительно операции *. Если (М,*) - моноид, а подмножество M' не только замкнуто относительно операции *, но и содержит нейтральный элемент, то M' называется подмоноидом в М.
21.4 Группа, абелева группа, подгруппа. X=Mn(R) - множество всех квадратных матриц с элементами из множества вещественных чисел. Y=Mn(R), det¹0 - множество квадратных матриц порядка n с определителем, не равным нулю. Ясно, что YÎX. Определим на множестве Y операцию умножения, тогда, если A,BÎY, то и ABÎY, EÎY, AE=EA=A для всех А из Y. Далее, для всякой матрицы А из Y имеется обратная матрица А-1,такая, что А-1А=АА-1=Е. Можно было бы сказать, что (X,×) - моноид, а (Y,×,E) - подмоноид, в котором каждый элемент обратим. Такой подмоноид имеет специальное название - группа. Группой называется множество G с одной алгебраической операцией, ассоциативной (не обязательно коммутативной) причем, для этой операции должна существовать обратная операция.Моноид G, все элементы которого обратимы, называется группой.Определение 3. Группа - это множество, построенное на 4-х аксиомах: 1) На множестве G определена бинарная операция: (xy)®x*y. 2) Операция ассоциативна: x(yz)=(xy)z. 3) Множество G обладает нейтральным элементом e: ex=xe=x для всех х из G. 4) Для всякого х из G существует обратный х-1Î G, xx-1=x-1x=e. Группа с коммутативной операцией называется коммутативной или абелевой группой. Подмножество НÌG называется подгруппой в G, если:1)Оно замкнуто относительно операции, определенной в группе, из h1, h2Î H следует h1*h2ÎH. 2)Включает в себя нейтральный элемент, еÎ Н.3) Включает в себя и обратные элементы, из hÎ H следует h-1Î H.
21.5 Пересечение групп. Если в группе G есть подгруппы А и В, то возможно их пересечение.Пересечение АÇВ - совокупность элементов принадлежащих одновременно и А и В, т.е. из принадлежности х к АÇВ следует принадлежность х к А и х к В. Пересечение АÇВ всегда является подгруппой в G. Доказательство: Пусть x,y принадлежат АÇВ, следовательно, x,y принадлежат А, следовательно, x*y принадлежит А, но x,y принадлежат В,т.к. и В - подгруппа, следовательно, и x-1, y-1 принадлежат и А и В,т.е, АÇВ - подгруппа. Это утверждение можно распространить на пересечение любого числа подгрупп.
21.6 Степень элемента и циклические группы. Понятие. Если n любое натуральное число, то "произведение" n элементов, равных а, называется n-ой степенью элемента а и обозначается аn. Под словом произведение имеется в виду результат выполнения введенной в группе операции. Только ассоциативность позволяет ввести понятие степени! При отсутствии ассоциативности бинарной операции а*(а*а)¹(а*а)*а. Если группа аддитивная, то роль степени выполняет кратное - na. Под нулевой степенью будем понимать нейтральный элемент a0=e=1, 0a=0 (е - нейтральный элемент в мультипликативной группе, 0 - нейтральный элемент в аддитивной группе). Под отрицательной степенью можно понимать: (аn)-1 или а-1а-1...а-1, что одно и тоже. Утверждение. В любой группе G, с любой операцией, соответствующей определению группы, для всех элементов а, принадлежащих группе, при любых показателях m,n - положительных, отрицательных, нулевых имеют место равенства:1) аnаm=аmаn=аm+n, 2) (аn)m=аmn. Циклические группы. Пусть дана группа (G,*,e). Пусть а - элемент этой группы. Рассмотрим множество {a}, составленное из всех степеней элемента а, т.е. аkÎ{a} при любом k. Сам элемент а=а1 принадлежит этому множеству, е=а0 также принадлежит этому множеству. Если аk, аlÎ{a}, то ak*al=ak+lÎ{a}, (an)-1=a-nÎ{a}, a-k, a-lÎ{a}, следовательно, a-k*a-l=a-(k+l)Î{a}. Мы доказали, что множество {a} - подгруппа в группе G при любой определенной в ней операции (умножение, сложение, и т.д.). а - образующий элемент. подгруппы.Подгруппа {a} называется циклической подгруппой группы G, порожденной элементом а. Утверждение. Циклическая подгруппа всегда коммутативна (абелева), даже если сама группа некоммутативная. (Следует из определения степени).
22 Изоморфизм групп. Изоморфизм - похожесть. Принципиально это понятие применимо к любой алгебраической структуре. Оно характеризует две похожие структуры и наличие отображения одной структуры в другую, при котором результат операции в первой структуре отображается в результат соответствующей операции с соответственными элементами во второй структуре. Отображение – это закон, по которому для каждого элемента в одной структуре отыскивается соответственный элемент в другой структуре. Отображение может быть однозначным (биективным) или неоднозначным (небиективным). Определение. Две группы (G,°) и (G',*) с операциями ° и * называются изоморфными, если существует отображение f: G ® G' такое, что 1) f(a°b)=f(a)*f(b) для всех a,b из G. 2) f - биективно или взаимно однозначно. Подробнее: a,bÎ G a°b Î G f: a®a' a°b®a'*b' или f(a)=a';f(b)=b' a',b'ÎG' a'*b'Î G' f: b®b' f(a°b)=a'*b' а это и означает, что f(a°b)=f(a)*f(b) для любых а,b из G. Теорема. 1) Все бесконечные циклические группы изоморфны между собой. 2) Все конечные циклические группы одного порядка изоморфны между собой. Доказательство: а) Бесконечная циклическая группа с образующим элементом а - {a},состоящая из всех степеней аn (n - любое целое число) отображается на множество (Z,+) - аддитивную группу целых чисел, если всякому элементу аk этой группы ставится в соответствие число k. ak, alÎ {a}; ak ® k; al ® l; k,l Î Z; akal0=ak+l ® k+l т.е. f(akal)=k+l=f(ak)+f(al). Это соответствует определению изоморфизма. б) Пусть G - конечная циклическая группа порядка n с образующим элементом а. Пусть e - первообразный корень n-ой степени из 1. Поставим в соответствие всякому ak из G, 0£k£n корень ek. Изоморфизм этого отображения следует из свойств:1) ak=ar, где k=nq+r; 2) anam=an+m. Это будет взаимно однозначное отображение группы G на мультипликативную группу корней n-ой степени из 1.Свойства изоморфизма. Пусть f: (G,°) ® (G',*) - изоморфизм. При этом а,е G, e - нейтральный элемент, т.е. a°e=e°a=a. 1. При изоморфизме нейтральный элемент переходит в нейтральный. Пусть f(a)=a', f(e)=e', но f(a°e)=f(a)*f(e)=a'*e'=a' следовательно, е' - нейтральный f(e°a)=f(e)*f(a)=e'*a'=a' элемент в G'.2.Обратный элемент переходит в обратный. a°a-1=e, f(a°a-1)=f(e)=e',отсюда f(a)*f(a-1)=e' - это как раз и означает, что f(a-1) - обратный к f(a), т.е. f(a-1)=(f(a))-1 или a'*(a')-1=e' (т.к. f(a)=a'). И наоборот: (f(a))-1=(f(a))-1*e'=(f(a))-1*f(a°a-1)==(f(a))-1*[f(a)*f(a-1)]=[(f(a))-1*f(a)]*f(a-1)=f(a-1). 3. Обратные отображения f-1; G' ® G (существуют в силу биективности) также изоморфны. f-1: (G',*) ®(G,°); надо доказать, что f -1(a'*b')=f-1(a')°f -1(b'), но f-1(a'*b')=f -1(f(a)*f(b))=f-1(f(f°b))=a°b=f-1(a')°f -1(b'). Пример изоморфизма: G=(R+, ×) - мультипликативная группа положительных вещественных чисел. G'=(R,+) - аддитивная группа всех вещественных чисел. Отображение f=ln. a,bÎG, ln ab=lna+lnb. Обратное отображение: любому хÎG' соответствует еx Î G.
22.1 Симметрические группы. Пусть W - конечное множество из n элементов любой природы. Их нумерация: W={1,2,...n}. Группа всех взаимно однозначных отображений W®W (множества на себя), f(W) называется симметрической группой степени n. Ее элементы называются перестановками. 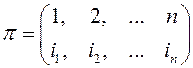 Операция их умножения некоммутативная. В любой группе n! перестановок, т.е. порядок группы Sn Сard Sn=|Sn|=n! Среди них есть единичная. Теорема Кэли. Любая конечная группа порядка n изоморфна некоторой подгруппе симметрической группы Sn степени n. Пусть G - наша группа порядка n, т.е. |G|=n - конечная, в ней n элементов. В группе Sn n! элементов, т.е. ее порядок n!, |Sn|=n!. Теорема Кэли утверждает, что G изоморфна какой-то части, подгруппе группы Sn и дает способ построить эту подгруппу. Пронумеруем все элементы нашей группы G (их n штук) и обозначим:е=g1, g2,...gn. Рассмотрим отображение La: G ® G, определяемое формулой: La(g)=ag,где а - любой фиксированный элемент из G. Т.е. g ® ag. Тогда наша группа преобразуется в группу: a, ag2,...agn - это все те же элементы, но расположенные в другом порядке, т.к. группа конечная. Таким образом, каждому элементу группы соответствует перестановка, определенное расположение всех элементов группы, в котором данный элемент находится на первом месте. Обратному элементу а-1 соответствует обратная перестановка (L-1)=La-1. «Произведению» элементов ab соответствует произведение перестановок ab ® LaLb = Lab, (La (Lb(g))=La (bg)=abg=Lab(g)). Нейтральному элементу е соответствует нейтральная перестановка: е ® Le, т.к. ea=a, Le(La(g))=Le(ag)=eag=ag=La(g). Данное отображение биективное, т.к. все La – различные, из равенства La=Lb следует: a=b, т.к. La(gi)=Lb(gi) ® agi=bgi, но все элементы группы обратимы, следовательно, agigi-1=bgigi-1 ® a=b. Таким образом, данное отображение – изоморфизм. Но
Операция их умножения некоммутативная. В любой группе n! перестановок, т.е. порядок группы Sn Сard Sn=|Sn|=n! Среди них есть единичная. Теорема Кэли. Любая конечная группа порядка n изоморфна некоторой подгруппе симметрической группы Sn степени n. Пусть G - наша группа порядка n, т.е. |G|=n - конечная, в ней n элементов. В группе Sn n! элементов, т.е. ее порядок n!, |Sn|=n!. Теорема Кэли утверждает, что G изоморфна какой-то части, подгруппе группы Sn и дает способ построить эту подгруппу. Пронумеруем все элементы нашей группы G (их n штук) и обозначим:е=g1, g2,...gn. Рассмотрим отображение La: G ® G, определяемое формулой: La(g)=ag,где а - любой фиксированный элемент из G. Т.е. g ® ag. Тогда наша группа преобразуется в группу: a, ag2,...agn - это все те же элементы, но расположенные в другом порядке, т.к. группа конечная. Таким образом, каждому элементу группы соответствует перестановка, определенное расположение всех элементов группы, в котором данный элемент находится на первом месте. Обратному элементу а-1 соответствует обратная перестановка (L-1)=La-1. «Произведению» элементов ab соответствует произведение перестановок ab ® LaLb = Lab, (La (Lb(g))=La (bg)=abg=Lab(g)). Нейтральному элементу е соответствует нейтральная перестановка: е ® Le, т.к. ea=a, Le(La(g))=Le(ag)=eag=ag=La(g). Данное отображение биективное, т.к. все La – различные, из равенства La=Lb следует: a=b, т.к. La(gi)=Lb(gi) ® agi=bgi, но все элементы группы обратимы, следовательно, agigi-1=bgigi-1 ® a=b. Таким образом, данное отображение – изоморфизм. Но 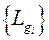 при i=1,2,…,n – подгруппа группы Sn. В этой подгруппе n элементов, её порядок n. Теорема Кэли позволяет в дальнейшем исследовать, как универсальный объект, семейства конечных групп - семейства симметрических групп {Sn, n=1,2,...n}, как вместилище всех конечных групп с точностью до изоморфизма. Отсюда, в частности, следует, что любая симметрическая группа Sn порядка n! разбивается, как минимум, на (n-1)! подгрупп порядка n.
при i=1,2,…,n – подгруппа группы Sn. В этой подгруппе n элементов, её порядок n. Теорема Кэли позволяет в дальнейшем исследовать, как универсальный объект, семейства конечных групп - семейства симметрических групп {Sn, n=1,2,...n}, как вместилище всех конечных групп с точностью до изоморфизма. Отсюда, в частности, следует, что любая симметрическая группа Sn порядка n! разбивается, как минимум, на (n-1)! подгрупп порядка n.
22.3 Автоморфизм. Если в определении изоморфизма мы положим G=G', то получим автоморфизм - изоморфное отображение группы на себя. Тривиальное единичное отображение группы на себя - автоморфизм.
22.4 Ядро гомоморфизма. Отображение f: G ® G', группы (G,*) в группу (G',°) называется гомоморфизмом, если f(a*b)=f(a)°f(b), для всех a,bÎG. Т.е. для гомоморфизма не требуется биективности. Множество элементов группы G может отобразиться в один элемент группы G'.Ядром гомоморфизма отображения f называется множество ker f: ker f={gÎG|f(g)=e'ÎG'}. Т.е. множество элементов из G, каждый из которых отображается в нейтральный (единичный) элемент из G'. Главное отличие гомоморфизма от изоморфизма - наличие нетривиального (т.е. состоящего не из одной единицы е) ядра ker f, являющегося мерой неоднозначности, неинъективности. Если ker f={e}, то G ® G' - изоморфизм. Пусть H=ker f Ì G, пусть a,b Î H, т.е. f(a)=e', f(b)=e', тогда f(a*b)=f(a)°f(b)=e'°e'=e', т.е. a*bÎH и f(a-1)=(f(a))-1=(e')-1=e', т.е. из aÎH следует a-1ÎH. Значит, H=ker f является подгруппой в G. Возьмем любой элемент hÎH и любой элемент gÎG. Сделаем отображение f произведения ghg-1, т.е.: f(ghg-1)=f(g)f(h)f(g-1)=f(g)e'f(g-1)=f(g)(f(g))-1=e' для любых hÎH и любых gÎG, значит, (ghg-1)ÎH. Можно доказать также, что (g-1hg)ÎH. т.е. gHg-1Ì H, g-1HgÌH и HÌ gHg-1, т.е. gHg-1=H для всех gÎG. Подгруппы, обладающие этими свойствами, называются нормальными инвариантными подгруппами или нормальными делителями. Мы доказали теорему: Теорема. Ядра гомоморфизмов всегда являются нормальными подгруппами. Пример 1. G=(Mn(R) det¹0, ×); G'=(R, ×,x¹0), т.е.: G - группа квадратных матриц порядка n, c det ¹0; G' - группа не равных нулю вещественных чисел. Обе группы мультипликативные. Отображение: f=det, т.е. матрице соответствует число из G'. Условие изоморфизма выполняется: f(A)×f(B)=f(A×B); detA×B.=detA×detB. Небиективность очевидна: у множества матриц может быть один и тот же детерминант. Ker f=Mn(R)det=1 - ядро гомоморфизма.
23.1 Понятия, примеры колец. Определение 1. Множество К называется кольцом, если в нем определены две операции - "сложение" и "умножение", обе ассоциативные, а также связанные законом дистрибутивности, причем сложение обладает обратной операцией - вычитанием. (Коммутативность умножения необязательна).Определение 2.Пусть К - непустое множество с двумя бинарными алгебраическими операциями: "сложением" и "умножением", удовлетворяющее условиям: 1. (К,+) - абелева группа, 2. (К, ×) - полугруппа (нет обратной операции), 3.Операции связаны дистрибутивным законом, Тогда К - КОЛЬЦО. Если ab¹ba, кольцо некоммутативно, Если ab=ba, кольцо коммутативно.Свойство дистрибутивности (распределительности) - несимметрично. Только дистрибутивность умножения относительно сложения позволяет различать эти операции: в числовых кольцах (a+b)c=ac+bc - привычно, но (ab)+c=(a+c)(b+c) - абсурдно. Кроме приведенных примеров числовых колец, еще примеры: - Совокупность чисел вида a+b 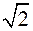 , где a,bÎQ - кольцо. При b=0 к нему относится и всё кольцо Q. (Сужение кольца Q). - Совокупность чисел вида a+b
, где a,bÎQ - кольцо. При b=0 к нему относится и всё кольцо Q. (Сужение кольца Q). - Совокупность чисел вида a+b 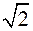 , где a,bÎZ - кольцо. (Расширение кольца Z). - Вместо
, где a,bÎZ - кольцо. (Расширение кольца Z). - Вместо 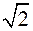 можно взять
можно взять 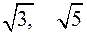 , и т.д. - это все будут кольца. - Числа вида а0+а1p+а2 p2+...+аnpn, где а0,a1,...an Î Q - кольцо. Нечисловые кольца: - множество всех многочленов от х, коэффициенты которых принадлежат к фиксированному числовому кольцу. - совокупность функций, определенных для всех хÎR и принимающих действительные значения, причем f(x)+g(x)=h(x) - такая функция, что h(x0)=f(x0)+g(x0) для всех х0, аналогично f(x)g(x)=h(x) - такая функция, что h(x0)=f(x0)g(x0) для всех х0. Антипримеры: - система положительных чисел (любая) - не содержит разности. - система отрицательных чисел (любая) - не содержит произведения. - система чисел вида
, и т.д. - это все будут кольца. - Числа вида а0+а1p+а2 p2+...+аnpn, где а0,a1,...an Î Q - кольцо. Нечисловые кольца: - множество всех многочленов от х, коэффициенты которых принадлежат к фиксированному числовому кольцу. - совокупность функций, определенных для всех хÎR и принимающих действительные значения, причем f(x)+g(x)=h(x) - такая функция, что h(x0)=f(x0)+g(x0) для всех х0, аналогично f(x)g(x)=h(x) - такая функция, что h(x0)=f(x0)g(x0) для всех х0. Антипримеры: - система положительных чисел (любая) - не содержит разности. - система отрицательных чисел (любая) - не содержит произведения. - система чисел вида 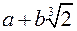 где a,bÎQ или Z - не кольцо, т.к.не содержит в себе произведения
где a,bÎQ или Z - не кольцо, т.к.не содержит в себе произведения 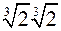 .система нечетных чисел - не содержит в себе суммы 2-х нечетных чисел и т.д. В любом кольце структура (К,+) называется аддитивной группой кольца, а (К,+) - его мультипликативной полугруппой. Если (К, ×) - моноид, то говорят, что (К,+,×) - кольцо с единицей.Подмножество L кольца К называется подкольцом, если из принадлежности любых x,yÎL следуют принадлежности x±yÎ L, x×yÎL, т.е. если L - подгруппа аддитивной группы и подполугруппа мультипликативной полугруппы кольца К. Пересечение любого семейства подколец - снова подкольцо.
.система нечетных чисел - не содержит в себе суммы 2-х нечетных чисел и т.д. В любом кольце структура (К,+) называется аддитивной группой кольца, а (К,+) - его мультипликативной полугруппой. Если (К, ×) - моноид, то говорят, что (К,+,×) - кольцо с единицей.Подмножество L кольца К называется подкольцом, если из принадлежности любых x,yÎL следуют принадлежности x±yÎ L, x×yÎL, т.е. если L - подгруппа аддитивной группы и подполугруппа мультипликативной полугруппы кольца К. Пересечение любого семейства подколец - снова подкольцо.
23.2 Кольцо классов вычетов. Два целых числа n и n' называются сравнимыми по модулю m (по mod m), если при делении на m они дают одинаковые остатки. Пример: Пусть m=5, тогда 16@51(mod 5).Таким образом, множество целых чисел Z разбивается на классы чисел, сравнимых между собой по модулю m (m N - натуральные числа), которые называются классами вычетов по mod m.
Пример:
Пусть m=6. Каждый класс вычетов имеет вид:
{0}6={0,6,12,18,24,....} {r}m=r+mz={(r+mk),kÎZ}.
{1}6={1,7,13,19,25,....} Все кольцо целых чисел разбилось на
{2}6={2,8,14,20,26,....} m непересекающихся классов:
{3}6={3,9,15,21,27,....} Z={0}m {1}m {2}m {3}m...{m-1}m.
{4}6={4,10,16,22,28,...}
{5}6={5,11,17,23,29,...} Определим "сложение" классов:
{k}m + {l}m={k+l}m при k+l<m;
{k}m + {l}m={k+l-m}m при k+l ³ m.
24.1 Понятие, примеры полей. Oпределение1. Поле Р - это коммутативное кольцо с единицей, 1¹0,в котором каждый элемент а¹0 обратим. Определение 2. Поле - это множество, содержащее в себе сумму, произведение, разность и частное от деления одного элемента на ненулевой другой элемент. Определение 3. Поле - это гибрид двух абелевых групп – аддитивной и мультипликативной, связанных законом дистрибутивности.В поле имеют место привычные правила действия с дробями при операциях "+" и "-", как в обычных операциях сложения и вычитания дробей. Определение. Подполем F поля Р называется подкольцо в Р, само являющееся полем. Q - поле рациональных чисел, подполе поля R - вещественных чисел. R - поле вещественных чисел - подполе поля С - комплексных чисел. Или: R - расширение поля Q, C - расширение поля R. Это примеры бесконечных полей.Вернемся к классам вычетов {r}m. Если m - простое число, то {r}m - поле. Нужно лишь доказать возможность деления в этом кольце и однозначность этой операции, т.е. возможность нахождения для любых k, l (l ¹ 0) третьего элемента х, такого, что xl=k, тогда мы разделим k на l, т.е. найдем х=k/l. Пример: {r}5: {1}5:{4}5={x}5 ® {4}5{x}5={1}5 ® {x}5={4}5. Или: {2}5:{3}5={x}5 ® {3}5{x}5={2}5 ® {x}5={4}5.
24.2 Пример конечного поля - поле Галуа. Составим поле Галуа из 4-х элементов, GF(4): a, b - какие-то алгебраические элементы, подчиняющиеся следующим законам "сложения" и "умножения":Gf(4):
“+” 0 1 a b “×” 0 1 a b
0 0 1 a b 0 0 0 0 0
1 1 0 b a 1 0 1 a b
a a b 0 1 a 0 a b 1
b b a 1 0 b 0 b 1 a






