Элементер ұяшықта бір немесе бірнеше атом орналасуы мҥмкін. Егер ұяшықта бір атом орналасса, онда тор түйінін осы атоммен біріктіруге болады. Бұл жағдайда тор Бравэ торы немесе қарапайым тор деп аталады. Егер ұяшықта бірнеше атом орналасса, онда торды бір-біріне енгізілген бірнеше қарапайым
торлар түрінде көруге болады. Онда тор а1, а2, а3 (наверху вектор нарисуйте) векторларымен және А базистік векторлармен сипатталады. А базистік векторлар а1, а2, а3 (наверху вектор нарисуйте) векторлары бар торға қатысты қосымша қарапайым торлардың ығысуымен анықталады.Кристалда тек қана жеті нүктелік симметриялықтүрлену жүзеге асады. Олар:
1) инверсиясы бар,
2) 5-ші, 7-ші не одан жоғары ретті осьтер болмайды,
3) 3-ші, 4-ші немесе 6-шы ретті симметрия осьтері арқылы өтетін симметрия жазықтығы бар. Барлығы Браве торларының 14 түрі бар. Браве торлары 4 үлгіге бөлінеді:
Примитивті – түйіндер параллелепипедтің тек төбелерінде орналасады.Базоцентрленген – екі карама-карсы жіктердің ортасында тағы бір түйіні болады.Көлемцентрленген – примитивті үлгіге ұяшықтың ортасына түйін косылған. Жікцентрленген – әр жіктің ортасында бір түйіннен болады.
Браве торлары келесідей сингонияларға бөлінеді: триклинная — 1, моноклинных — 2, тетрагональных — 2, ромбических — 4, тригональная (ромбоэдрическая) — 1, гексагональная — 1, кубических — 3.Сингонии: кубическая — куб со сторонами a = b = c и углами между ними α = β = γ = 90°;
тетрагональная — параллелепипед a = b ≠ c, α = β = γ = 90°;
ромбическая — параллелепипед a ≠ b ≠ c, α = β = γ = 90°;
тригональная - a = b = c, α =β = γ ≠ 90°;
гексагональная — состоит из трех призм с основанием в фо
рме ромба a = b ≠ c, α = β = 90°, γ = 120°;
моноклинная — параллелепипед a ≠ b ≠ c, α = γ = 90°, β ≠ 90°;
триклинная — косоугольный параллелепипед a ≠ b ≠ c, α ≠ β≠ γ ≠ 90°.
24.Дебайжылусиымдылығыжәне оның шығарылуы
Дебайдың айтуы бойынша кристалдық торда атомдардың тербелісі бір - біріне тәуелсіз емес. Бір атомның тепе – теңдік қалпынан шығуы басқа атмодардың тепе – теңдік қалпынан шығуына алып келеді. Сонымен кристал N рет серпімді байланысқан материалды нүктелерден тұратын жүйені құрайды, s=3N еркіндік дәрежесі бар.Бірлік көлемдегі фонондық газдың U энергиясы:
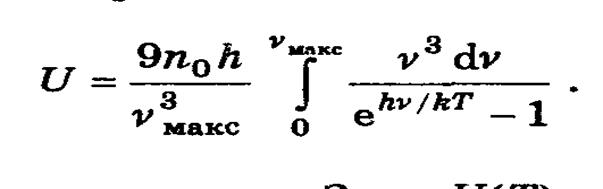
U(T)біле отыра біз бірлік көлемдегі кристалдың жылусыйымдылығын жаза аламыз.
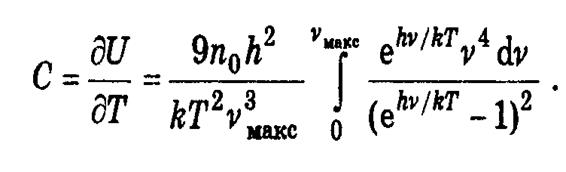
Дебайдың темперауралық сипатттамасын енгіземіз:һνмакс=kΘ
Жаңа айнымалыны енгіземіз x=һν/kT Сонда жылусыйымдылық жаңа түрге ие болады.
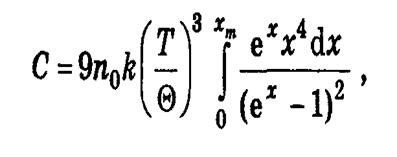
- Дебай формуласы
Бұл жерде xm= һνмакс/kT =Θ/T тең. Сондай–ақ жылусыйымдылықтан басқа Дебай температурасы Θ тербелістің энергиясын квантауға болатын температуралық аймақты көрсетеді.Жылусыйымдылықтың C(T) шектік жағдайда байқалынатын құбылстары:
1.T<<Θ болған T3 кезде интегралдың жоғарғы шегі xm→∞ мынаған тең болады қарастыра аламыз. Сонда интеграл білгілі бір санға ие болады да, C~T3
Бұл нәтижені Дебайдың заңы деп атаймыз. T<<Θболған кезде C-ның T-дан дәл осындай тәуелділігі эксперименттен байқалады.
2. Т>>Θ болған кезде һνмакс/kT<<1 тең болғанда, U үшін оңайлатып eһν/kT≈1+ һν/kT
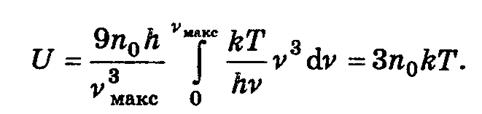
жаза аламыз. Сонда
Кристалдың 1 молі үшін n0 на NA ауыстырып, кристалдың молярлық жылусыйымдылығын жаза аламыз: C=3R
Дюлонг Пти заңымен сәйкес келу керек нәрсе сәйкес келді. Жазылған теңдеулер әмбебап емес. C(T) тәуелділігі кристалдық торы қарапйым келетін қатты денелерге ғана орындалады, күрделі құрылымды қатты денелерге Дебай формуласы қолданылмайды. Оны ары қарай зерттемейміз, тек бұл мәселе кванттау арқылы шешілгенін білсек жеткілікті.
25.Кері тордың векторы және оның қасиеттері
Кері тор — бастапқы кеңістік тордың (100), (010), (001) координаталық торлары оларға нормаль координаталық осьтермен алмастырылған қосымша құрылыс. Кері тор кристаллографияның есептеу әдістерінде көп қолданылады.
Кристаллдарды сипаттау үшін кері тор деген түсінік жиі пайдаланылады. Кері торды былай анықтаймыз:
А = т 1 а 1 + т 2 а 2 + т3 а – теңдеуімен берілген нүктелер жиынымен тура тор анықталса, оған сәйкес кері торды былай анықталады:
В =n1 b1 + n2 b 2+n3 b 3 (1)
Мұндағы
n1, n2, n3 – бүтін сандар,
b1, b2, b3 – кері тордың негізгі векторы.
Кері тордың негізгі векторының формуласы мынадай:
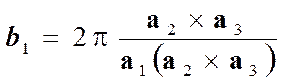(2)
b2, b3 – векторларын табу үшін индекстерін циклді ауыстыру керек. (2) – теңдеуінің бөліміндегі өрнек тура тордың Va элементар көлемін көрсетеді. Егер тура тор тік бұрышты немесе орторомбалық, тетрагонал, әлде куб формалы болса, онда:
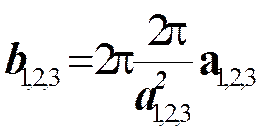и 
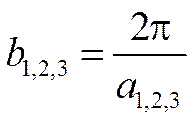(3)
Кері тор анықтамасынан келесі маңызды қасиеттерді тұжырымдауға болады:
1) а i b j =2ij, мұндағы ij —Кронекердің дельта-символы:
ij=1 егер i=j жәнеij=0 егер ij; (4)
2) кері тордың элементар көлемі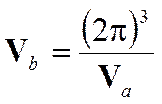 
; (5)
3) Кері торға кері тор, ол тура тор болады;
4) Тура тор мен кері тордың кез-келген векторларының скаляр көбейтіндісімынадай: AB =2 n (6)
мұндағы п — бүтін сан, яғни ехр(i АВ) =1.
Әрбір В кері тор векторына, оған перпендикуляр болатын, бір – бірінен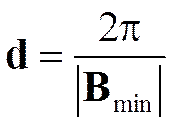 
бірдей қашықта жатқан жазықтықтар жиыны сәйкес келеді.
26.Ферми энергиясы және оның толқын векторына тәуелділігі
Абсолют ноль Кельвиндегі электронның ең үлкен энергиясын Ферми энергиясы деп атайды. Ферми деңгейі — жартылай бүтін спины 6aр бөлшектер (фермиондар) жүйесінің абсолют нөл температурада бос және толтырылған энергетикалық деңгейлерін бөліп тұратын энергияның мәні SF (Ферми энергиясы). Фл түсінігі шалаөткізгіштердің өткізгіштігін түсіндіретін аймақтық теориялар қолданылады: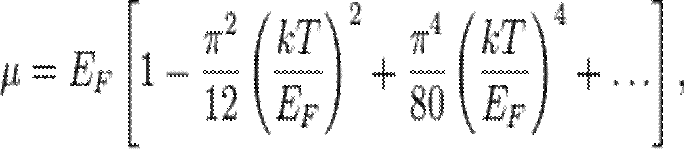 
27.Вульф-Брегг тендеуі, оны дәлелдеу
Дифракция құбылысының пайда болуы үшін, көршілес жазықтықтар арасындағы ара қашықтық кристалда сәуле пайда болуы, түскен сәуле толқын ұзындығының жартысынан кем болмауы қажет. Рентген сәулелердің дифракциясы газдарда, сұйықтықтарда және аморфты заттарда, әсіресе кристалдарда айқын байқалады. Рентген сәулелердің дифракциясындағы кристалдар негізінде, кейінірек рентген құрылымдық және рентгенофазалық талдау әдістері өңделген. Рентген сәулелерінің дифракция мәні - екінші қайтара толқындардың толқын жиіліктерінің өзгеруінсіз зерттеліп жатқан атомның электрондық қабықшасындағы құраушылар, яғни электрондармен шашыратылған амплитудаларының қосуында жатыр. Рентген сәулелерінің рұқсат етілген шашырау бағыттарының кеңістік шашырауының саны мен сипаттамасы Ю. Вульф пен У. Брег (1913) келесідей қатынастағы заңымен анықталады: 2dsin = nλ (5)
мұндағы d– кристалдағы шағылатын көршілес жазықтықтың арасындағы ара қашықтық;
υ– кристалға түсетін жарықтың шағылу бетінің бағытымен пайда болатын сырғанау бұрышы;
n– берілген 
және 
-да дифракциялық максимумбақыланатын, реттік шағылу;
λ – рентгендіксәулеленудіңтолқындықұзындығы.
Егерзерттелетін кристалл, монохроматты (λ =const) рентгендікжарықжолындаорналасқанболса, оны жарықтың перпендикуляр осібойыншаайналдырыпжәнеосылайша, шағылатынжағдайғарет ретіменкристалдыңжазықтықжүйесінқойсақ, онда, шашыраудыңтолықсуретібақылады. Рентгендіксәулеленудіңүздіксізспектрініңкөзінқолданаотырып, дифракциялықсуреттіүлгіайналуынсыз да алуғаболады. Бұлжағдайдабарлығына кристалл жазықтығыныңжүйесіүздіксізспектрдеміндеттітүрде, Вульф – Брегтіңзаңынқанағаттандыратын λ толқынұзындығытабылады.
Пусть плоская монохроматическая волна любого типа падает на решётку с периодом d, под углом θ, как показано на рисунке
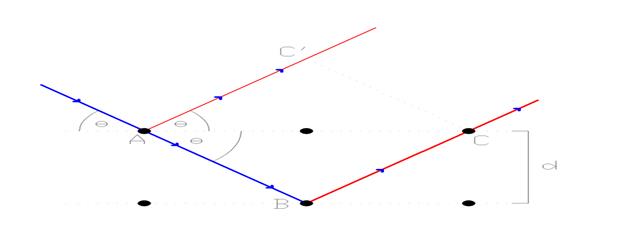
Как видно есть разница в путях между лучом, отражённым вдоль AC' и лучом, прошедшим ко второй плоскости атомов по пути AB и только после этого отражённым вдоль BC. Разница в путях запишется как (AB+BC)-(AC ')
Если эта разница равна целому числу волн n то две волны придут в точку наблюдения с одинаковыми фазами, испытав интерференцию. Математически можно записать:
(AB+BC)-(AC)=n λ
где λ — длина волны излучения. Используя теорему Пифагора можно показать, чтоAB=d/sinӨ; ВС=d/sinӨ; AC=2d/tanӨ
как и следующие соотношения:AC=AC*cosӨ=(2d/tanӨ)*cosӨ
Собрав всё вместе получим известное выражение:
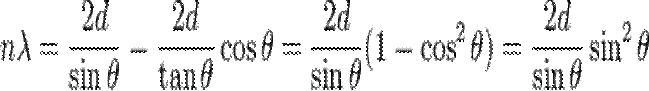
После упрощения получим закон Брэгга
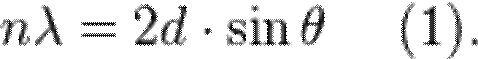
28.Ферми бос электрондық газдың байланыс энергиясы
Ферми-Дирактың таралу функциясына бағынатын электрондар үшін Т=0 болғанда Е<Ef облысында энергияның барлык куйлері электрондармен толық толығу тән. Қорытынды: сырттан әсер бергенде электрондар өз энергиясын жоғарылатады немесе төмендетеді. Бүкіл электрондар жиынын бөтелкені толтырып тұрған сұйық ретінде қарастыруға болады. Сыртқы ықпал, мысалы, қыздыру тек сұйық бетін буландыруға ғана алып келеді немесе осы бөтелкеден сұйық ағуын қарастыруға болады. Ол бөтелкенің аузынан ғана ағады. Сол сияқты электрондар да тек Ферми деңгейінен «буланады» немесе «ағады». Қатты дене қасиеттерінің көпшілігі сыртқы күштердің тек Ферми бетінде «орналасқан» электрондармен әрекеттесуіне тәуелді болғандықтан, бұл беттерді білу табиғаты әртүрлі қатты денелер үшін өте маңызды. Ферми бетінің түрі қатты дененің қасиеттерін анықтайды. Сол қасиеттер электрондар ауысумен байланысты, мысалы, электрөткізгіштік, жылуөткізгіштік және т.б.
29. Шектік симметрия топтары. Оны қалай түсінесіз
Кристалдың морфологиялық симметриясы мен олардың физикалық қасиеттерінің байланысын зерттеген кезде шекті топтардың маңызы зор. Француз физигі П.Кюри физикалық қасиеттерді зерттеген кезде симметрия заңдылықтарын қолдануға мүмкіндігін талдай отырып шекті топ ұғымын енгізді.Шексіз (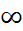
) симметрия осьтері бар нүктелік симметрия топтары шекті симметрия топтары немесе Кюри топтары д.а. Шекті топтарды нүктелік топтар сияқты стереографиялық проекция түрінде бейнелеуге болмайды, өйткені симметрия элементтері проекциясының шексіз санын бейнелеу анық емес. бірақ олардың ерекшеліктерін айқындау материалдық кеңістік фигураларда оңай іске асыруға болады. Шекті симметрия топтарының саны 7-ге тең: ∞, ∞/2, ∞/m, ∞m, ∞/mm, ∞/∞, ∞/∞m. Симметрия осінің реті жоғарылаған сайын кеңістік фигуралардың барлық нүктелік симметрия топтары шексіздікте осы топтардың біреуіне ұмтылады.Шекті симметрия топтарын зерттеген кезде нүктелік симметрия топтарының шағын топшалары деп аталатын жаңа ұғым енгізіледі.Нүктелік топтың барлық симметрия элементтері бастапқы симметрия тобында табылатын болса, онда оны нүктелік топтың шағын топшасы д.а.Осы анықтама бойынша жоғарыда қарастырылған кеңістік фигуралардың барлық нүктелік топтары симметрия осьтерінің реті жоғарылағанда ұмтылатын өз шекті топтарының топшалары болып табылады.
30.Блох теоремасыжәне оның шығарылуы
Теорема Блоха — важная теорема физики твёрдого тела, устанавливающая вид волновой функции частицы, находящейся в периодическом потенциале. Названа в честь швейцарского физика Феликса Блоха. В одномерном случае эту теорему часто называют теоремой Флоке.
Собственные состояния одноэлектронного гамильтониана
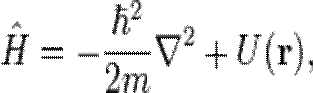
где потенциал U (r) периодичен по всем векторам R решётки Бравэ, могут быть выбраны таким образом, чтобы их волновые функции имели форму плоской волны, умноженной на функцию, обладающую той же периодичностью, что и решётка Бравэ:
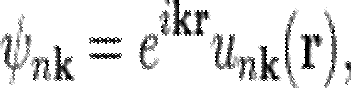
где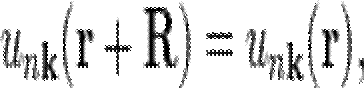 
для всех R, принадлежащих решётке Бравэ. Индекс n называют номером зоны. Его появление связано с тем, что при произвольном фиксированном волновом векторе частицы k, система может иметь много независимых собственных состояний.В теореме рассматривается идеальный бесконечный кристалл. Это означает, что в нём отсутствуют дефекты и он обладает трансляционной симметрией. При дальнейшем построении теории, нарушения периодичности решётки обычно считаются малыми возмущениями. Кроме того, в реальном кристалле электроны взаимодействуют между собой, что должно отразиться на гамильтониане системы добавлением соответствующего члена. В формулировке теоремы, однако, используется приближение невзаимодействующих электронов, что позволяет рассматривать одночастичный гамильтониан.
