При наложении распространяющихся навстречу монохроматических волн одинаковой частоты, амплитуды (например, прямой и отражённой) образуются стоячие волны.
s(t,x)=Acos[w (t–x/c)]–Acos[w (t+x/c)]=2Asin[w x/c]sinw t
В каждой точке порисходит гармоническое колебание с частотой w, причём амплитуда зависит от положения точки по закону: А(х)=2А|sin[wx/c]|
Акустическая волна – это периодическое возмущение плотности среды, распространяющееся в среде со скоростью звука. Периодические возмущения плотности среды называются акустическими колебаниями. Акустические колебания бывают продольными (колебания вдоль направления распространения волны) и поперечными (колебания в плоскости, перпендикулярной направлению распространения волны).
Стоячая акустическая волна – это акустическая волна, которая является суперпозицией прямой и отраженной волны в ограниченной среде. Распределение амплитуды стоячей волны (пучности и узлы) зависит от физических параметров среды и граничных условий.
Акустический резонатор – это устройство, предназначенное для получения резонанса акустических колебаний в среде, заполняющей устройство. Акустический резонатор имеет ряд собственных резонансных частот, каждая из которых имеет собственную добротность и, соответственно, затухание. Ряд колебаний на резонансных частотах резонатора называются модами резонатора.
Распространенные примеры:
 |
Камертон – устройство для настройки музыкальных инструментов, издающее звук, высота которого соответствует одной из семи нот музыкального ряда.. Для камертона важным является не только долгое (малое затухание) и чистое звучание, но и возбуждение только одной из мод этого резонатора. Именно форма камертона позволяет возбуждать колебание только одной моды с высокой добротностью. Остальные моды имеют низкую добротность колебаний.
Кварцевый резонатор – это устройство, где в качестве акустической среды используется пластинка кристаллического кварца. Пластинка хорошо отполирована, грани выполнены с высокой степенью параллельности. Длины волн собственных мод колебаний описывабтся уравнением
L = n lр/2,
где lр- длина волны, которая может испытывать резонанс при длине резонатора L, n – целое число.
Билет № 27.
Опр. Работой силы на перемещении называется поекция этой силы на направление перемещения, умноженная на перемещение. dA = FdS = FdScosa.
Если сложить все элементарные работы и перейти к пределу, устремив к 0 длинны всех элементарных перемещений, а их число к µ, то такой предел обозначается символом: 
, и наз. криволинейным интегралом вектора F вдоль траектории L. Элементарная работа результирующей 2-х или нескольких сил равна сумме элементарных работ этих сил.
F=dp/dt, ds=v dt Þ A=ò(v dp)=[p=mv, v dp=mv dv, скалярное произведение самого на себя равно квадрату длинны]=mv2/2. A12=m 
, речь идёт о работе при перемещении материальной точки из положения 1 в положение 2. Величина K=(mv2/2)=p2/2m наз. кинетической энергией материальной точки. Работа силы при перемещении материальной точки равна приращению кинетической энергии этой точки. Кинетической энергией системы наз. сумма кин. эе. м.т., из к-х эта система состоит.
Как преобразовыается кинетическая энергия из одной системы в другую? Скорости связаны соотношением: v=v’+V Þ (Mv2)/2 = (mv’2)/2 + (mV2)/2 + mv’V
или K =K’+(mV2)/2+(p’V), где р’=mv’ – импульс материальной точки в системе S’.
Это справедливо и для системы м. т. (мы можем рассмотреть их по две) K=K’+(mV2)/2 + m(Vv’)/2
Это теорема Кёнига:
Кинетическая энергия системы м. т. равна сумме кин. энергии всей массы системы, мысленно сосредоточенной в её центре масс и движущейся вместе с ним, и кин. энергии той же сиситемы в её относительном движении по отнош. К поступательно движущейся системе с началом в центре масс.
Билет № 28.
 |
Момент импульса. Тензор инерции. Момент импульса тела относительно неподвижной точки – важнейшее понятие в динамике вращательного движения твердого тела. Он определяется так же, как и для системы материальных точек:
Здесь Dpi=mivi – импульс элементарной массы dmi в лабораторной системе XYZ, а ri – радиус-вектор массы dmi с началом в той неподвижной точке, относительно которой вычисляется момент импульса тела. С учетом постоянства расстояний между точками абсолютно твердого тела вектор момента импульса L удается связать с вектором угловой скорости w.Рассмотрим, к примеру, две одинаковые точечные массы m, укрепленные на концах невесомого стержня АВ (рис. 2.3). Стержень с массами вращается с угловой скоростью w вокруг вертикальной оси, проходящей через середину стержня и перпендикулярной ему. В этом случае:
L=mri´vi+ mr2´v2=2mr2w, здесь учтено, что: r1 =r2 =r, а v1=v1=wr.
 |
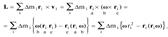Существенно, что в этом примере век тор L направлен так же, как и w. К сожалению, так бывает не всегда. В этом можно убедиться на примере, показанном на рис. 2.4. Получим выражение для L в случае твердого тела произвольной формы, закрепленного в некоторой точке О. Пусть ri – радиус-вектор элементарной массы Dmi твердого тела, а w –угловая скорость. Тогда:
Векторы ri, w и L можно проектировать как на оси лабораторной системы XYZ, так и на оси системы xyz, жестко связанной с твердым телом (поскольку точка О неподвижна, начала обеих систем можно совместить). Преимущество системы xyz заключается в том, что в ней проекции r i являются постоянными величинами (в системе XYZ они зависят от времени), и выражения для компонент L оказываются проще.
ваются центробежными моментами инерции. Если Jxy=Jyx, Jxz=Jzx, Jzy=Jyz, то тензор наз. симметричным.
Если оси Ox, Oy, Oz совместить с главными осями инерции, то тензор инарциипримет дигональный вид. Величины Jxx=Jx, Jyy=Jy, Jxx=Jz в этом случае наз. главными моментами инерции тела, причём: Lx=Jxwx и т. д. Эти оси также называются главными осями тензора инерции. Они жестко связаны с телом.
Направление главных осей тела часто можно определить, пользуюсь соображениями симметрии. Так, например, главные оси однородного прямоугольного параллелепипеда параллельны его рёбрам. К телам такого рода относится, например цилиндр.
Оси свободного вращения. Вращательное движение – это такое, при котором две точки тела остаются всё время неподвижными. Прямая, проходящая через эти точки, называется осью вращения. Все точки твердого тела, лежащие на оси вращения, неподвижны. Другие точки твердого тела движутся по окружностям в плоскостях, перпендикулярных оси вращения. Центры этих окружностей лежат на оси вращения. Вращательное двизение твердого тела является плоским. Осевые мометы инерции Jxx, Jyy, Jxx.
Билет № 29.
Свободная ось вращения тв. Тела – такая ось, которая не испытывает деформации под влиянием центробежных сил инерции.
Главные – такие оси, в которых тензор инерции оказывается приведенным к диагональному виду.
Центральные – такие оси вращения, которые проходят через центр масс тела.
Главные оси и свободные оси не одно и тоже. Центральные оси и свободные оси не одно и тоже. Главная центральная ось и свободная ось одно и тоже. Наиболее устойчивое такое вращение твердого тела, когда его момент инерции максимален. Вторым по устойчивости является такое вращение твердого тела, когда его момент инерции минимален. Вращение вокруг оси с промежуточным моментом инерции является наименее устойчивым. Когда твердое тело вращается вокруг одной из его главных осей, векторы N и W коллинеарны. При скатывании цилиндра мгновенная ось вращения совпадает с той образующей цилиндра, которая соприкасается с наклонной плоскостью.
Пункт 2.
Акустическая волна – это периодическое возмущение плотности среды, распространяющееся в среде со скоростью звука. Периодические возмущения плотности среды называются акустическими колебаниями. Акустические колебания бывают продольными (колебания вдоль направления распространения волны) и поперечными (колебания в плоскости, перпендикулярной направлению распространения волны).
Стоячая акустическая волна – это акустическая волна, которая является суперпозицией прямой и отраженной волны в ограниченной среде. Распределение амплитуды стоячей волны (пучности и узлы) зависит от физических параметров среды и граничных условий.
Звуковые (акустические) волны - упругие волны в воздухе, частоты которых лежат в пределах от 20 до 20 000 колебаний в секунду.
Ж и газы обладают только объёмной упругостью. В них возможны только продольные волны. Рассмотрим участок газа, сечения s, длины dx.
 |
r0 s dx ¶2S/¶t2 = [Px – Px+dx] s
r0 ¶2S/¶t2 = - ¶P/¶x
При малых изменениях давления у положения p0:
dP=(¶P/¶r)r0 dp=c2 dr
-¶P/¶x=-c2 ¶dr/¶x=–c2 ¶/¶x[r0 (-¶S/¶x)]=c2ro ¶2S/¶x2
¶2S/¶t2 = c2 ¶2S/¶x2, c2= ¶P/¶r, при r=r0
Зависимость от температуры:
P=rRT/m P=const rg g=Ср/СV dP/dr= g const rg-1= g P0/r0 Þ
Þ C2=g P0/r0= g RT/m
Пусть плоская акустическая волна возбуждается бесконечной пластинкой, колеблющейся в направлении x по закону 
.
Тогда волна распространяется также в направлении x, смещение частиц, лежащих в любой плоскости, нормальной к этому направлению, происходит по з-ну: 
.
Относительное изменение толщины слоя, лежащего между двумя бесконечно близкими пл-тями: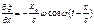 
.
Этому изменению расстояния соответствует такое же относительное изменение обьема, заключенного между двумя пл-тями. 
(5)
Скорость частиц: 
.(6)
Из (5) и (6) Þ 
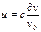(7)
dv/v0=–dr/r0 (8)
dp/dr=g p0/r0
Из (8),(9) Þ Dp= g p Dr /r =g pu/c=r cu, т.к. (1). (10)
Интенсивность. Звуковая волна несет с собой потенциальную энергию - энергию упругой деформации газа и кинетическую энергию движущихся частиц газа. Подсчитает потенциальную энергию, заключенную в элементе обьема SDx. Если относительное сжатие в слое есть h= dv/v0, то по (10) сила, действующая на стенку площади S, есть SDp =ghp. При изменении относительного сжатия на dh стенка перемещается на Dx× dh и при этом совершается работа dA=S×Dx×gp×h×dh.
u=SDxg p 
Плотность энергии упругой деформации wU=g ph2/2 (14)
Кинетическая энергия этого же обьема T=r SDxu2/2 и плотность кинетической энергии wT= ru2/2. Из (7) видно, что wU=wT. Тогда плотность всей энергии звуковой волны w=gp×h2. Т.к. h меняется как cos, то h2 меняется как cos2, значит h2ср=h02/2, wср =g ph02/2. Т.к. (7) выполняется для всяких мгновенных значений Dз и h, то оно справедливо и для амплитудных значений и Þ wср =(Dp0)2c/2g p, где Dp0 - амплитуда звукового давления.
Энергия, которая падает за единицу времени на единицу площади, нормальной к направлению распространения звуковой волны, называется интенсивностью звуковой волны.
Интенсивность звука I= wср c=(Dp0)2c/2g p = =(Dp0)2/2r c (т. к. с2=g p/r) Интенсивность звука измеряется в дж/см2×с.
Билет № 30.
Пункт 1.
Движение твердого тела с одной неподвижной точкой. В этом случае тело имеет три степени свободы – начала систем XYZ и x 0 y 0 z 0, введенных в начале лекции, можно совместить с точкой закрепления, а для описания движения тела использовать три угла Эйлера: j=j(t), y=y(t), q=q(t).
Для твердого тела с одной неподвижной точкой справедлива теорема Эйлера: твердое тело, закрепленное в одной точке, может быть переведено из одного положения в любое другое одним поворотом на некотjрый угол вокруг неподвижной оси, проходящей через точку закрепления. Cледствие из этой теоремы: движение закрепленного в точке твердого тела в каждый момент времени можно рассматривать как вращение вокруг мгновенной оси, проходящей через точку закрепления. Положение этой оси как в пространстве, так и относительно самого тела с течением времени общем случае меняется. Г М положений мгновенной оси вращения относительно неподвижной системы XYZ (или x 0 y 0 z 0) – это сложная коническая поверхность с вершиной в точке закрепления. В теоретической механике ее называют неподвижным аксоидом. Г М положений мгновенной оси вращения относительно подвижной системы xyz, жестко связанной с твердым телом, – это тоже коническая поверхность – подвижный аксоид. Линейная скорость произвольной точки твердого тела вокруг мгновенной оси: v=w´r, где r – радиус-вектор точки относительно начала системы XYZ (или x 0 y 0 z 0), совмещенного с точкой закрепления.
Пункт 2. Эффект Доплера. Движение источника звука, сопровождающееся изменением расстояния от источника до приёмника,приводит к изменению частоты принимаемого звука. Это связано с тем, что скорость распространения звуковой волны в среде не зависит от скорости движения источника. Поэтому, если источник звука движется от приёмника со скоростью v см/сек, то за единицу времени мимо приёмника пройдут не все максимумы, а только часть их: приёмник отметит меньшее число колебаний, чем создаёт источник. Убедиться в этом можно при помощи элементарного расчёта. Пусть источник в начале секунды находился на расстоянии с см от приёмника, с см/сек –скорость звука в среде, тогда через секунду он будет находится на расстоянии с+v см на этом расстоянии уложатся все f максимумов которые за 1 сек созданы излучателем (f-частота), но за 1 секунду до приёмника дойдут не все максимумы, а часть на расстоянии с см f’=f/(1+v/c) –частота полученная приёмником,если приёмник приближается то f’=f/(1-v/c); если же вдижется приёмник, а не источник,то если приёмник движется к источнику со скоростью v то за 1 сек он пройдёт не f, а f ‘’ максимумов, где f’’=f(1+v/c) если удаляется то f‘’=f(1-v/c);
