ентробежная и кориолисова силы инерции. Примеры проявления их действия.

илет № 1.

Механика – наука о движении и равновесии тел. При построении теории физика заменяет реальные обьекты их идеализированными моделями. Движение – это изменение относительнеого положения тела с течением времени. Впервые принципы механики сформулированы Ньютоном в «Математических началах натуральной философии».

Тело или система тел, относительно которых определяется положение остальных тел называется простанственной системой отсчета (ПСО). В качестве ПСО можно взять произвольное твердое тело и связать с ним координатные оси, например, декартовой системы координат. Существует два вида координатных систем: 1) правая, 2) левая. Определяются они с помощью правила буравчика.

Пространство (по Ньютону) – это совокупность физического тела и возможных его продолжений.

Время – это показание каких-то часов (под часами понимается любое тело или система тел, в которых совершается периодический процесс, служащий для измерения времени).

Кинематика занимается изучением движение тела не абстрагируясь на его причины.

Движение материальной точки будет описано полностью, если известно ее положение в любой момент времени относительно выбранной системы отсчета. Полное описание движения сводится к нахождению трех координат: x = x(t); y = y(t); z = z(t); или к нахождению векторной функции r = r(t). . – мгновенная скорость. Производная скорости по времени называется ускорением материальной точки: ,

Уравнение кинематической связи –уравнение связывающее кинематические характеристики тел системы.

Закнон движения – это зависимость координат точки от времени. Закон движения можно рассматривать как уравнение траектории где t параметр.(уравнение траектории – уравнение кривой по которой движется точка.)

Материальная точка – это тело, размеры которого пренебрежимо малы, что в рассматриваемом движении их можно не принимать во внимание и считать, что все вещество тела как бы сосредоточено в одной точке. Материальная точка – это абстракция, идеализированный образ реально существующих тел.

Система мат. Точек – некоторая совокупность их числа.

Пункт 2.

Гироскоп – массивное аксиально-симметричное тело, вращающееся с большой угловой скоростью вокруг оси симметрии.

Гироскопическая сила – сила, действующая на опору со стороны быстро вращающихся масс.

Если гироскоп раскручен вокруг оси симметрии, то L=Jw=const и направление оси симметрии остаётся неизменным. Прецессия гироскопа.(к оси гир. приложена сила, линия действия которой не проходит через точку закрепления).

Ось гироскопа перемещается не в направлении сил, а перпендикулярно к ней. Элементарная теория гир.(мгн. угловая скорость вращения и мом. импульса направлены вдоль оси симметрии, w>>W). Мом. импульса: L=J_zw (J_z – мом. ин. относительно оси симметрии) Рассмотрим гир, у которого точка опоры S не совпадает с центром масс О. Мом силы тяжести: M=mglsinq, где q - угол между вертикалью и осью симметрии. dL=M*dt, при этом и ось и L прецессируют вокруг вертикали с угл скоростью W. dL=L sinq W dt dL= WxL dt M=WxL Для силы тяжести: mgl sinq = WJ_zw sinq угл скорость прецессии W=mgl/ J_zw. Если сообщить гироскопу толчок, изменяющий угол q, то прецессия перестанет быть равномерной (часто говорят: регулярной), а будет сопровождаться мелкими колебаниями вершины гироскопа – нутациями. Вектор момента импульса L описывает неподвижный в пространстве конус прецессии, и при этом ось симметрии гороскопа движется вокруг вектора L по поверхности конуса нутации. Вершина конуса нутации, как и вершина конуса прецессии, находится в точке закрепления гироскопа, а ось конуса нутации совпадает по направлению с L и движется вместе с ним. Угловая скорость нутации определяется выражением w_нут=L/J_s@J_zw/J_s где J_z и J_s - моменты инерции гироскопа относительно его оси симметрии и относительно оси, проходящей через точку опоры и перпендикулярной оси симметрии, w - угловая скорость вращения вокруг оси симметрии. Раскрутим гироскоп вокруг его оси симметрии до большой угловой скорости (момент импульса L) и станем поворачивать раму с укрепленным в ней гироскопом вокруг вертикальной оси с некоторой угловой скоростью W. Момент импульса L получит при этом приращение dL, которое должно быть обеспечено моментом сил М, приложенных к оси гироскопа. Момент М, в свою очередь, создан парой сил F+ F`, возникающих при вынужденном повороте оси гироскопа и действующих на ось со стороны рамы. По третьему закону Ньютона ось действует на раму с силами Ф + Ф`. Эти силы называются гироскопическими, они создают гироскопический момент М`. Появление гироскопических сил называют гироскопическим эффектом. Именно эти гироскопические силы мы и чувствуем, пытаясь повернуть ось вращающегося колеса.

Гироскопический момент нетрудно рассчитать. Положим, согласно элементарной теории, что L=Jw Где J – момент инерции гироскопа относительно его оси симметрии, а w - угловая скорость собственного вращения. Тогда момент внешних сил, действующих на ось, будет равен M=WxL=Wx(Jw) Где W – угловая скорость вынужденного поворота (иногда говорят: вынужденной прецессии).Со стороны оси на подшипники действует противоположный момент M`=-M= (Jw)xW Направление гироскопических сил можно найти легко найти с помощью правилa, сформулированного Н.Е.Жуковским гироскопические силы стремятся совместить момент импульса L гироскопа с направлением угловой скорости вынужденного поворота.

илет № 2.

Сложение 2 движений точки. r=R+r’ – где R радиус вектор начала штрихованной системы отсчета отн не подвижной.

Vabs=V+[W*r’] +v’ –где v’- относит. Скорость V+[W*r’] – переносная скорость.

a=A+[b*r’]+[w[w *r’]]+2[w*v’]+a’- где первые 3 слагаемых переносное ускорение, 2[w*v’]-кориолисово ускорение,a’-относительное ускорение.

Пункт 2.

Деформации тел. Опыт показывает, что под действием приложенных сил тела в той или иной степени меняют свою форму и объем, что на микроскопическом уровне означает относительное смещение атомов, составляющих тело. Такие изменения называются деформациями. В случае твердых тел различают два предельных случая: деформации упругие и деформации пластические. Упругими называют деформации, исчезающие после прекращения действия приложенных сил. Пластическими или остаточными деформациями называют такие деформации, которые сохраняются в теле, по крайней мере частично, и после прекращения действия внешних приложенных сил. Если напряжение (сила, отнесенная к единице площади) не превосходит предела упругости, то возникающая деформация будет упругой. Для удобства описания деформаций мысленно разобьем тело на физически малые объемы (иногда их будем называть частицы), содержащие, однако, большое число атомов. В отсутствие деформаций атомы находятся в состоянии теплового равновесия, а все малые объемы — в механическом равновесии. Тогда сумма сил и моментов сил, действующих на выделенный объем со стороны примыкающих к нему других объемов, будет равна нулю. Изменения положений атомов при деформациях приводят к тому, что в теле возникают внутренние силы, или внутренние напряжения, стремящиеся вернуть тело в состояние равновесия. Только соседние атомы или молекулы эффективно взаимодействуют друг с другом.

Типы деформаций. Коэффициент Пуассона. При всем многообразии случаев произвольную деформацию тела можно свести к двум элементарным деформациям — растяжению (сжатию) и сдвигу. При растяжении резинового шнура его поперечный размер d уменьшается до величины d₁. Такое поперечное сжатие характеризуется параметром e_^=(d₁–d)/d=Dd/d. Продольный размер изменяется на D l и характеризуется величиной e=(l₁–l)/ l=Dl/l. Опытным путем установлено, что отношениек e_^ к e приблизительно одинаково для разных деформаций одного и того же материала. Поэтому в теории упругости материал характеризуется коэффициентом Пуассона:

m=–(e_^/e)

Подсчитаем численное значение коэффициента Пуассона? Чтобы ответить на этот вопрос, подсчитаем изменение объема резинового шнура:

V= l d², V₁= l₁d₁²=l(1+e)d²(1+e_^)²= [раскроем скобки и пренебрегём e_^², 2ee_^, ee_^²]»V(1+e+2e_^)

DV/V=(V₁–V)/V»e+2e_^=e(1-2m).

илет №3.

Система отсчёта, в которой все свободные тела движутся прямолинейно и равномерно называется инерциальной.

Утверждение впервые высказанное Г. Галилеем, о том, что во всех инерциальных системах координат механические явления протекают одинаково, называется принципом относительности Галилея. В дальнейшем в результате изучений других явлений, в частности электромагнитных, справедливость этих положений была признана для любых явлений. В таком общем виде оно называется принципом относительности СТО или просто принципом относительности

Преобразования Галилея. Рассмотрим систему отсчета, либо неподвижную, либо движущуюся с постоянной скоростью и с единым временем. Для этих систем справедлив принцип относительности Галилея. Имеется система отсчета К и система отсчета К^’, которая движется со скоростью V относительно системы К.

[x; y; z; t x^’; y’; z’; t’]

Условия: 1. Все оси систем параллельны друг другу. 2. Скорость движущейся системы параллельна оси Ox.3. Ускорение, угловое ускорение, угловая скорость равны 0. 4. R=0 при t=0. 5. часы в обоих системах одинаковы.

Физическая сущность этого преобразования составляет принцип относительности Галилея

1. t = t^’

2. DL = DL’ (длины отрезков одни и те же).

Следующие преобразования отражают механический принцип относительности:

x^’ = x – vt; y^’ = y; z^’ = z; t^’ = t

Обратные преобразования: x = x^’ + vt; y = y^’; z = z^’; t = t^’

(из них можно получить закон сложения скоростей)

Уравнения, остающиеся неизменными при переходе от одной системы отсчета к другой, называются инвариантными.

События, одновременные в одной системе, одновременны и в другой, т. е. утверждение об одновременности двух событий имеет абсолютный характер, независимый от системы координат.

Длинна – инвариант преобразований Галилея. Длиной движущегося стержня наз. расстояние между координатами его концов в некоторый момент времени. Следуя из этого инвариантность длинны легко доказывается.

Интервал времени явл. инвариантом преобразований Галилея (Dt=t₂–t₁=t’₂–t’₁=Dt’)

Сложение скоростей получается из дифференцирования формул преобразования Галилея.

Ускорение инвариантно относительно преобразований Галлилея. Это утверждение доказывается дифференциированием преобразований скорости и учитывая, что Dt=Dt’.

Пункт 2.

Рассмотрим, например, растяжение (или сжатие) стержня под действием силы F, приложенной перпендикулярно к торцевой грани с площадью сечения S. При последовательном возрастании нагрузки вначаледеформации развиваются равномерно по длине стержня и растут пропорционально нагрузке: e=(l₁–l)/ l=F/SE=s/E. Величина s =F/S называется нормальным напряжением в торцевом сечении стержня. Пропорциональность деформаций e соответствующим напряжениям выражает закон Гука. Е – модуль Юнга. Закон Гука окончательно записывают в виде e=s/Е.

Опыт показывает, что этот закон выполняется лишь в определенном интервале напряжений. При некотором напряжении появляется заметное остаточное удлинение. Это напряжение s называется пределом упругости. Закон Гука выполняется только в части области упругости — области пропорциональности. При возрастании нагрузки наблюдается явление текучести, т.е. рост удлинения образца при постоянной нагрузке, называемой пределом текучести. Отметим, что течение материала происходит равномерно по всей длине стержня. За пределами области текучести дальнейшее удлинение стержня сопровождается увеличением s. Однако деформации будут распределены уже неодинаково по длине стержня — в некотором месте можно заметить образование шейки. При напряжении sM, называемом пределом прочности, в этом ослабленном сечении происходит разрыв. Аналогичными оладают и деформации сдвига. Вобласти пропорциональности связь между деформацией и касательным напряжением задаётся соотношением: g=F/(GS)=s_t/G, где s_t=F/S – касательное напряжение, а G – модуль сдвига.

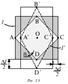
Установим зависимость G от Е. Обратим внимание на то, что квадратная грань ABCD параллелепипеда (рис. 1.9), находящегося внутри рассматриваемого кубика, превращается при деформации в ромбическую грань A’B’C’D’. Совершенно ясно, что параллелепипед испытывает сдвиговую деформацию, а его объем при этом практически не изменяется. Величину угла сдвига a можно легко связать с деформацией удлинения e=D l/l и коэффициентом Пуассона m=–e_^/e. Из треугольника A'OD’ следует, что:

 

Поскольку b <<1, то

 

В последней формуле учтено, что em << 1. Сила F, растягивающая кубик (рис. 1.10), создает нормальное напряжение s=F/ l ². Это напряжение передается на грани AB и BC параллелепипеда, однако силы, действующие на каждую из граней, имеют не только нормальную к грани, но и направленную вдоль грани составляющую F_t. Касательное напряжение оказывается при этом равным: 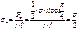(1.24) Поскольку деформации e в формуле (1.23) пропорциональны напряжениям, а s=2s_t, то: a=2(1+m)s_t/E. Сравнивая последнее равенство с соотношением g=F/(GS)=s_t/G и учитывая, что g=tga»a, получаем то, что искали: G = E /2(1+m).

Тело над которым совершают работу обладает запасом потенциальной энергии. Эту энергию и называют упругой энергией. Энергия растянутого стержня U=1/2k(dl)^2=1/2F*dl

илет № 4.

1) Всякое тело оказывает сопротивление при попытках изменить модуль или направление его скорости. Это свойство тел называется инертностью. Масса - мера инертности.

2) Изолированная система – система тел, настолько удаленных от всех остальных тел, что они практически не оказывают действия на рассматриваемую систему.

Рассмотрим изолированную систему из двух материальных точек (их скорости много меньше скорости света). Dv₁, Dv₂ - приращения скоростей м.т. за одинаковый Dt. Из опыта: m₁ Dv₁ =–m₂ Dv₂,где m₁, m₂ - положительные величины, не зависящие от характера взаимодействия между м.т., от Dv₁ и Dv₂, а зависящие только от самих м.т. Тогда m₁, m₂ – инертные массы м.т. 1 и 2.

Импульс: p =m× u - импульс м.т. Импульс системы м.т. - p = p₁ + p₂ +...+ p_n

Сила - любая причина, изменяющая импульс движущегося тела (мера взаимодействия). Одно из количественных определений: m r ¢¢= F.

Законы Ньютона:

I. Существуют такие системы отсчета, в которых изолированная точка движется прямолинейно и равномерно (инерциальные системы отсчета).

II. (уравнения движения м.т.): (m u) ¢= F. (в исо)

III. Силы взаимодействия двух м.т. равны по модулю, противоположны по направлению и действуют вдоль прямой, соединяющей их.

Ш закон Ньютона содержит в себе 5 утверждений. 1. Силы в природе всегда возникают парами, это силы взаимодействия. 2. Они равны по величине. 3. противоположны по направлению. 4. действуют вдоль одной прямой. 5. имеют одинаковую природу.

Закон всемирного тяготения. Этим законом определяется сила F притяжения между точечными телами, находящимися на расстоянии r друг от друга, в виде: F=Gm₁m₂/r².

Закон Гука. Для деформируемого, тела при упругих деформациях в области пропорциональности: F=–kx.

Пункт 2. Под действием внешних сил в жидкостях и газах, как и в твердых телах, могут возникать внутренние напряжения. Рассматривая жидкости и газы как сплошные среды, мы отметим, что жидкости, не имея определенной формы, сохраняют практически неизменный объем. Во многих важных случаях их можно рассматривать как несжимаемые. Газы же не имеют ни определенной формы, ни фиксированного объема.

В жидкости при сжатии силы отталкивания между молекулами могут быть весьма значительными. По этой причине говорят не о растягивающих и сдвиговых напряжениях s_ij, а о давлениях р_ij= - s_ij как об отрицательных напряжениях. Совокупность давлений р_ij, действующих на площадки, перпендикулярные осям координат и ограничивающие кубический элемент жидкости, называется тензором давлений.

В покоящейся или медленно движущейся жидкости тангенциальные напряжения p_ij (i¹j), связанные с вязкостью отсутствуют.

Закон Паскаля. Внешнее давление передается жидкостью и газом по всем направлениям если в них отсутсвует сила трения покоя.

Если пренебречь силами тяготения, действующими на каждый элементарный объем жидкости, то из условия равновесия этого объема следует, что p₁₁ = p₂₂ = p₃₃ = p (1) При этом давление p, возникающее вследствие внешнего воздействия, является скалярной величиной и одинаково во всех точках объема, занятого покоящейся жидкостью. Условие (1) автоматически обеспечивает не только равенство нулю суммы сил давления, приложенных к данному объему, но и равенство нулю суммарного момента этих сил. Для доказательства этого условия рассмотрим неподвижную жидкость, помещенную в цилиндрический сосуд с площадью основания S₁, закрытый сверху поршнем.

 

 

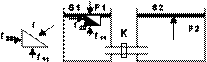
Если надавить на поршень силой F₁, то в жидкости будут созданы внутренние напряжения (давления). Рассмотрим условия равновесия элементарного объема жидкости, имеющего форму кубика. На единицу его поверхности будет действовать сжимающая сила f_ii=-p_iin_i, направленная противоположно нормали n_i к i-ой поверхности. Поскольку силы, действующие на противоположные грани кубика, равны по величине, то p₁₁=F₁/S₁. Равенство давлений р₁₁ и р₂₂ следует из условия равновесия половины кубика, выделенного более темным цветом и изображенного на фрагменте. Действительно, f₁₁= f₂₂ = f /(2)^0,5. Поэтому р₂₂=р₁₁. Рассматривая равновесие элементарных объемов в различных точках жидкости, получим условие: p_ii=p=F₁/S₁ которое является математическим выражением закона Паскаля.

Если рассмотренный сосуд соединить при помощи трубки с другим цилиндрическим сосудом с площадью основания S₂, то при открывании крана К внутренние напряжения в соответствии с законом Паскаля передадутся во второй сосуд. На поршень, закрывающий этот сосуд, жидкость будет давить вверх с силой

F₂ = pS₂ = (F₁/S₁)S₂ .

g=-(1/V)*dV/dP – коэффициент сжимаемости, характеризует упругие свойства жидкостей по отношению к малым деформациям. Коэфициент всестороннего сжатия – величина обратная коэфициенту сжимаемости.(оба коэфициента при T=const).

Билет № 5.

Сухое трение. Сила сухого трения покоя возникает на поверхности двух соприкасающихся тел и равна разности сил приложенных к телам. Если 2 поверхности движутся, то сила сухого трения пропорциональна силе нормального давления.

Сила вязкого трения. В случае силы сухого трения при сила, меньших силы трения скольжения 2 поверхности не движутся относительно друг друга, а вслучае вязкого трения какова бы ни была сила – возникнет движение, причем для малх скоростей силя вязкого трения пропорциональна скорости, а на больших скоростях её квадрату.

ункт 2.

По мере увеличения высоты давление и плотность монотонно убывают, а температура монотонно убывает лишь в нижнем десятикилометровом слое, а в более высоких слоях меняется немонотонно. Параметры атмосферы зависят как от географического положения места, так и от времени года. Сложная высотная зависимость температуры атмосферы есть результат совместного проявления процессов тепломассопереноса, инициируемых излучением Солнца.

Атмосфера делится на отдельные участки. Нижний слой атмосферы,называемый тропосферой,содержит 80% массы атмосферы, почти весь водяной пар и облака и характеризуется сильным вертикальным перемешиванием. Сверху тропосфера ограничена тропопаузой, где температура меняется очень мало. Выше расположена стратосфера,где температура повышается, и заканчивает повышаться в стратопаузе. Выше находится мезосфера, где температура опять падает. Выше находится термосфера, в которой температура опять растет до 600-2000 К. Для вычисления изменения атмосферного давления с высотой воспользуемся условием равновесия

Связь между давлением и плотностью задается уравнением состояния идеального газа , т. к. влияние влажности на плотность воздуха сущ. лишь в тропиках на поверхности и ошибка <2%.

Получаем ур-ие .

Которое можно проинтегрировать, если известно Т(х).

В качестве грубого приближения можно использовать среднее значение температуры 250 К.

Интегрируя получим барометрическую ф-лу: .

По этому же закону изменяется и плотность воздуха: .

Приведенная высота (высота на которой давление падает в е раз): .

Билет № 6.

Назовем импульсом или количеством движения материальной точки вектор, равный произведению массы точки на ее скорость: Р =m× v

Импульсом или количеством движения системы материальных точек назовем векторную сумму импульсов отдельных материальных точек, из которых эта система состоит.

Произведение постоянной силы F на время ее действия называется Импульсом силы за то же время.

Закон сохранения импульса. Импульс изолированной или замкнутой системы 2-х материальных точек сохраняется, т. е. остается неизменным во времени, каково бы ни было взаимодействие между ними. Это утверждение справедливо также и для изолированной с. м. т., состоящей из сколь угодно большого числа м. т.

Запишем третий закон Ньютона для замкнутой системы, состоящей из произвольного числа материальных точек.

F₁⁽ⁱ⁾+F₂⁽ⁱ⁾+…+Fn⁽ⁱ⁾=0, (1)

где Fn⁽ⁱ⁾ – полная внутренняя сила., действующая на n-ную точку. Обозначим далее символами F₁^(e),F₂^(e),… внешние силы, действующие на материальные точки системы. Тогда на основании второго закона Ньютона можно записать

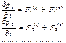
Сложив почленно эти уравнения и приняв во внимание соотношение (1) найдем

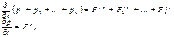(2)

где р- импульс всей системы,F^(e)-равнодействующая всех внешних сил, действующая на нее. Пусть теперь геометрическая сумма всех внешних сил равна нулю (Например, замкнутая система). Тогда (dp/dt)=0, или p=const.

Закон сохранения импульса является отражением фундаментального св-ва пространства - его однородности.

Изолированная система – система тел, настолько удаленных от всех остальных тел, что они практически не оказывают действия на рассматриваемую систему.

Замкнутая система – это система, удалённая от остальных тел, на которую не оказывается действие.

Пункт 2. На тела, погруженные в жидкость, действует выталкивающая сила, направленная вертикально вверх. Эта сила является результатом действия сил давления. Выталкивающая сила F_А, называемая силой Архимеда,может быть подсчитана при учете распределения давления по глубине и оказывается равной весу вытесненной жидкости. Извлечём из сосуда с жидкостью тело, затем дольём туда жидкости (той же). Выделим мысленно границы тела в жидкости и поймём, что сумма действ. сил на жидкость внутри условных границ =0 Þ Архимедова сила равна весу вытесненной жидкости. Центр масс погруженного тела может не совпадать с центром объема. Это несовпадение имеет большое значение для устойчивого плавания тел, погруженных в жидкость (в кораблестроении используется термин остойчивость).

Для тел, плавающих на поверхности жидкости, центр их тяжести всегда будет расположен выше центра объема, погруженного в жидкость, и остойчивость плавания достигается выбором подобающей формы корабля и его загрузки. В судостроении форму судна с учетом его загрузки рассчитывают таким образом, чтобы метацентр находился выше центра масс судна. Этот метацентр является центром кривизны кривой, проходящий через центры объемов погруженных частей корпуса корабля.,сменяющих друг друга при его боковой качке.

илет № 7.

В нерелятивистской механики импульс системы р может быть выражен через скорость ее центра масс. Центром масс или центром инерции системы называется такая воображаемая точка, радиус-вектор R которой выражается через радиусы-векторы r₁,r₂,… материальных точек по формуле

R=(m₁r₁+m₂r₂+…)/m, где m=m₁+m₂+….Если продифф. Выражение по времени и умножить на m то получится: , -скорость центра масс системы. Таким образом, p=mV. Подставив это в (2): Центр масс системы движется как материальная точка, масса которой равна суммарной массе всей системы, а действующая сила - геометрической сумме всех внешних сил, действующих на систему. В релятивистском случае потятие ц. м. не является инвариантным понятием, не зависящем от выбора системы координат, и поэтому не применяется. Для материальной точки з. с. импульса означает, что в отсутствии внешних сил она движется с постоянной скоростью по прямой линии. Для СМТ в нерелятивистском случае закон утверждает, что ц. м. движется равномерно и прямолинейно.

Под однородностью пространства понимается эквивалентность всех точек пространства друг другу. Это означает, что если имеется некоторая изолированная система, то развитие в ней не зависит от того, в точках какой области пространства эта система локализована. Если все точки системы сместить на Dr, то в состоянии системы ничего не изменится, т. е. работа внутренних сил системы =0. Dr Ввиду независимости взаимодействий каждой из пар точек друг с другом Þ F_ij+F_ji=0. Þ закон созранения импульса изолированной системы материальных точек обусловлен фундаментальным свойством пространства в ИСО –– его однородности. Отсюда можно заключить, что с однородностью пространства связан и принцип относительности.

Пункт 2. Рассмотрим стационарное течение жидкости в каком-либо консервативном силовом поле, например, в поле силе тяжести. Применим к этому течению закон сохранения энергии. При этом полностью пренебрегаем теплообменом между жидкостью и средой. Выделим в жидкости бесконечно узкую трубку тока и рассмотрим часть жидкости, занимающую объём MNDC. Пусть эта часть переместилась в бесконечно близкое положение M₁N₁D₁C₁. Вычислим работу А, совершаемую при этом силами давления. Давление, действующее на боковую поверхность трубки тока, перпендикулярно к перемещению и работы не совершает. При перемещении границы MN в положение M₁N₁ совершается работа А₁=P₁S₁L₁, где L₁=MM₁- величина перемещения. Введя объём D₁V=S₁L₁,ее можно представить в виде А₁=P₁DV₁ или А₁=P(D₁m/r₁), где D₁m- масса жидкости в объеме MNN₁M₁. При перемещении границы CD в положение границы C₁D₁ жидкость совершает работу против давления P₂. Для нее, рассуждая аналогично, найдём А₂ =P₂(D₂m)/r₂, где D₂m- масса жидкости в объеме CDD₁C₁. Но если движение стационарно, то масса жидкости в объеме M₁N₁DC не изменится, следовательно D₁m=D₂m=Dm, получим А=А₁-А₂=(P₁/r₁ -P₂/r₂) Dm. Эта работа = приращению DЕ полной энергии выделенной части жидкости. Ввиду стационарности течения энергия жидкости в объеме M₁N₁DC не изменилась. Поэтому величина DE= разности энергий массы жидкости Dm, в положениях CDD₁C₁ и MNN₁M₁. Находим DЕ=(e₂-e₁)Dm, где e - полная энергия, приходящаяся на единицу массы жидкости. Приравняв DE к А и сократив на Dm получим: e₁+P₁/ =e₂ +P₂/r₂ . Отсюда следует, что вдоль одной и той же линии тока при стационарном течении идеальной жидкости величина e+P/r остаётся постоянной: e+P/r=B=const-это отношение называется уравнением Бернулли. Оно справедливо и для сжимаемых жидкостей. Требуется только, чтобы жидкость была идеальной, а течение- стационарным.

Линия, касательная которой указывает направление скорости частицы жидкости, проходящей в рассматриваемый момент времени через точку касания, называется линией тока. Если поле скоростей, а следовательно, соответствующие ему линии тока не меняются с течением времени, то движ. жидкости называется стационарным или установившемся.

Возьмем произвольный замкнутый контур С и через каждую точку его в один и тот же момент времени проведём линии тока. Они расположатся на некоторой трубчатой поверхности, называемой трубкой тока. Так как скорости частиц жидкости направлены по касательным к линиям тока, то при течении жидкость не может пересекать боковую поверхность трубки тока. Масса жидкости, протекающая за время dt через попер. сечение трубки будет: dm=rvSdt. Если взять 2^А сечения S₁=S₂, то: r₁v₁S₁=r₂v₂S₂, если жидкость не сжимаема, то r₁=r₂ получится: (v₁/v₂)=(S₂/S₁). Скорость жидкости в одной и той же трубке тока тем больше, чем уже поперечное сечение трубки.

Билет № 8.

Уравнение движения тел с переменной не содержат ничего принципиально нового по сравнению с законами Ньютона, и являются их следствиями. Но они представляют большой интерес в связи с ракетной техникой.

Выведем уравнение движения материальной точки с переменной массой на примере движения ракеты. Пусть m(t)-масса пакеты в произвольный момент времени t, а v(t)-ее скорость в тот же момент. Импульс ракеты в этот момент будет mv. Спустя dt масса и скорость ракеты получат приращение dm и dv(dm-отрицательна). Импульс ракеты станет (m+dm)(v+dv). Сюда надо добавить импульс движения газов, образовавшихся за dt. Он равен dm_газv_газ –масса и скорость газа, образовавшихся за dt. Вычитая из суммарного импульса системы в момент t+dt импульс системы в момент t, найдем приращение этой величины за dt. Это приращение равно Fdt, где F – геометрическая сумма всех внешних сил, действующих на ракету. (m+dm)(v+dv)+dm­_газv_газ-mv = Fdt Время dt устремим к нулю. Поэтому, раскрывая скобки, отбрасываем dmdv. Далее dm+dm_газ=0 и v_отн=v_газ-v есть скорость истечения газов относительно ракеты. Тогда mdv = v_отнdm + Fdt, деля на dt m(dv/dt) =v_отн(dm/dt) + F (1)

Член v_отн(dm/dt) – реактивная сила. Уравнение (1)-уравнение Мещерского или уравнение движения точки с переменной массой.

Пусть теперь у нас F=0, тогда mdv = v_отнdm. Допустим, что ракета движется прямолинейно в направлении, противоположном скорости v_отн. Тогда проекция v_отн на направление движения будет –v_отн. Тогда dv/dm = -(v_отн/m) Пусть скорость газовой струи v_отн постоянна, тогда v= - v_отн ò(dm/m) = - v_отн ln(m) + C Значение С определяется начальными условиями. Если, в начальный момент времени скорость ракеты =0, а масса = m_0, тогда 0 = - v_отн­ ln(m₀) + C, откуда С = v_отн ln(m₀). Следовательно: v = v_отн ln(m/m₀) или m₀/m=e^{v / v отн} .(2)

Уравнение (2) – формула Циолковского. Она справедлива для нерелятивистских движений (v и v_отн­ << c) Релятивистская формула имеет вид: , где b= v/c.

Пункт 2.

Билет № 9.

Пункт 1. Смотри предыдущий билет.

Пункт 2.

Силы вязкого трения. Ньютон установил опытным путем, что при скольжении друг относительно друга двух параллельных плоскостей, пространство между которыми заполнено жидкостью, силы вязкого трения препятствуют этому скольжению (рис. 4.1). Эта сила пропорциональна площади S и изменению скорости на единицу длины в поперечном направлении h/v (градиенту скорости в направлении, перпендикулярном движению) и зависит также от вязкости жидкости m:. F=mSv/h. h²<<S. Важно отметить, что частицы жидкости, прилегающие к верхней пластине, движутся вместе с нею со скоростью v (увлекаются пластиной). Напротив, частицы жидкости вблизи нижней (неподвижной) пластины находятся в покое (прилипают к пластине). Представим, что жидкость между пластинами состоит из плоских параллельных слоев, движущихся равномерно (рис. 4.2). Нетрудно понять, что каждый вышележащий слой увлекает за собой нижний соседний слой с силой F. В свою очередь, этот нижний слой тормозит движение верхнего слоя с той же силой. На каждый слой действуют сверху и снизу две равные, но противоположно направленные силы. Скорость слоев возрастает от нижнего слоя к верхнему линейно (рис. 4.2), а силы трения, действующие на каждый из слоев, одинаковы. Как результат, усилие приложенное к верхней пластине, передается на нижнюю пластину.

Течение вязкой жидкости. Уравнение Навье-Стокса.

Для анализа течения вязкой жидкости в правую часть уравнения движения r(dv/dt)=F–drad p необходимо добавить силу вязкого трения, приложенную к единице объема жидкости. Для простоты ограничимся рассмотрением течения жидкости в направлении оси x, при это единственная компонента скорости vx будет зависеть от поперечной координаты y (рис. 4.3). На верхнюю грань dxdz кубика dxdydz (ось z перпендикулярна плоскости чертежа) в соответствии с F=(mSv/h) в направлении оси x действует увлекающая сила: 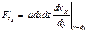, а на нижнюю грань тормозящая: 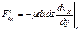. Равнодействующая сил вязкого трения, приложенная к выделенному кубику, равна F_t=F’_tx+F”_tx, a сила, приложенная к единичному объему, составит . В общем случае сила вязкого трения, вообще говоря, имеет три компоненты: f_t={f_tx, f_ty, f_tz}, где f_tx=mDv_x, f_ty=mDv_y, f_tz=mDv_z, где D= — оператор Лапласа, для сокращения записи. Если теперь компоненты силы трения подставить в правые части уравнений:

 

для соответствующих компонент скоростей, то мы получим систему уравнений гидродинамики вязкой жидкости. Эти три уравнения могут быть записаны в виде одного векторного уравнения Навье-Стокса:

Течение вязкой жидкости по трубе. Формула Пуазейля. Если мы подсоединим тонкую горизонтальную стеклянную трубу с впаянными в нее вертикальными манометрическими трубками при помощи резинового шланга к водопроводному крану (рис. 4.6). При небольшой скорости течения хорошо видно понижение уровня воды в манометрических трубках в направлении течения (h 1 >h 2 >h 3). Это, в свою очередь, указывает на наличие градиента давления вдоль оси трубки — статическое давление в жидкости уменьшается по потоку. При равномерном прямолинейном течении жидкости силы давления уравновешиваются силами вязкости. Уравнение Навье-Стокса для этого случая запишется в виде:

-grad p+mDv=0. (4.12)

Распределение скоростей в поперечном сечении потока вязкой жидкости можно наблюдать при ее вытекании из вертикальной трубки через узкое отверстие (рис. 4.7). Если, например, при закрытом кране К налить вначале неподкрашенный глицерин, а затем сверху осторожно добавить подкрашенный, то в состоянии равновесия граница раздела Г будет горизонтальной. Если кран К открыть, то граница примет форму, похожую на параболоид вращения. Приравняем нулю сумму сил вязкости и давления, действующих на цилиндрический объем жидкости радиуса r и длиной dx (рис. 4.8): (p(x) – p(x+dx))pr²+m2prdx(dv/dr)=0(4.13)

Отметим, что равнодействующая сил давления направлена по потоку (вдоль оси x), а сила вязкого трения, приложенная к боковой поверхности выделенного цилиндра — против потока, поскольку dv/dr<0. Произведя сокращение и разделив (4.13) на dx, получаем:

–(dp/dx)+2mdv/(rdr)=0 (4.14)

Величина градиента давления dx/dp в (4.14) не зависит от радиуса r, т.к. давление p=p(x) и в поперечном сечении x=const не меняется. Это позволяет проинтегрировать (4.14):

(4.15)

Поток вектора скорости через поперечное сечение трубы, или объем жидкости, протекающей через сечение в единицу времени (на практике употребляют термин «расход жидкости») оказывается равным: .

Для практических целей расход жидкости определяют по формуле Пуазейля: Здесь расход воды N_v пропорционален разности давлений p₁– p₂ на длину.

Билет № 10.

Пункт 2. Число Рейнолдса также определяет относительную роль инерции и вязкости: при больших числах Рейнольдса более важна роль инерции, при малых – вязкости.Силы вязкости,возникающие в потоке, обратно пропорциональны квадрату характерного поперечного размера потока и пропорциональны скорости. Давления р₁ и р₂ по разные стороны изогнутой трубки тока будут разные. Возникающий градиент давления связан с ускореним частиц жидкости уравнением: r(dv/dt)@–grad p Для частицы: F _и–grad p+mD v =0 Þ силы вязкости значительно меньше сил инерции. В общем случае силы инерции обратно пропорциональны поперечному размеру потока и пропорциональны квадрату скорости. Re=rvh/m – число Рейнольдса, характеризующее отношение сил инерции к силам вязкости. Re>1 Þ жидкость можно рассматривать как невязкую.

Ламинарным называется такое течение жидкости, когда её частицы двигаются вдоль траекторий параллельных стенам трубы. Особенностью ламинарного течения является его регулярность. Ламинарное течение может изменится только вследствии посторонних воздействий. При больших скоростях ламинарное течение становится неустойчивым и переходит в турбулентное. Турбулентное – это течение, гидродинамические характеристики, которого изменяются быстро и нерегулярно – флуктуируют. При ламинарном течении силы вязкости сглаживают боковые движения жидкости, возникающие вследствие флуктуаций и неровностей стенок трубы. При недостаточной вязкости случайные боковые движения жидкости усиливаются, способствуя тем самым возникновению турбулентности. Переход от ламинарного течения к турбулентному происходит при некотором числе Рейнольдса, получившем название критического: (Re)_КР=(rvR/m)_кр. Значение (Re)_КР сильно зависит от формы входной части трубы. При установившемся турбулентном течении скорость в данной точке случайным образом меняется современен, однако средняя скорость v направлена вдоль оси трубы. Она остается постоянной по сечению трубы, и только в очень тонком пограничном слое спадает до нуля у ее стенок. Для турбулентного течения жидкости по трубе p₁–p₂=kr<v²> l /R, где к – безразмерный гидравлический коэффициент. Для ламинарного течения: p₁–p₂=8m<v> l /R². Повышение скорости прокачки жидкости по трубам при турбулентном течении потребует значительно большнго увеличения перепада давлений, чем при ламинарном. Формулы можно объединить в одну, если принять, что безразмерный гидравлический коэффициент в зависит от числа Рейнольдса: k=k₀+(8/Re). Тогда при Re>Re_кр коэффициент k@k₀, и течение турбулентное. Напротив, при Re<1 k»8/Re, и первая формула переходит во 2-ую. На рис. (4.12) изображен график зависимости перепада давления в трубах от скорости течения. При свободном ламинарном течении жидкости (в отсутствие направляющих поверхностей) развиваются неустойчивости, и ламинарное течение переходит в турбулентное. На рис. 4.13. представлено изображение струи жидкости (число Рейнольдса Re = 250).

Тело в потоке вязкой жидкости. Лобовое сопротивление. Поток реальной жидкости или газа действует с некоторой силой на тело, помещенное в этот поток. Для осесимметричного тела с осью симметрии, направленной вдоль потока, эта сила также будет направлена вдоль потока. Она получила название силы лобового сопротивления. Основные физические причины возникновения лобового сопротивления можно установить наиболее просто, если рассмотреть обтекание потоком шара радиуса r. На рис. 4.21. изображена зависимость силы лобового сопротивления от числа Рейнольдса. При малых скоростях течения, когда Re<10² F_||~v, т. к. на шар действуют силы вязкости, возникающие вследствие существования тонкого пограничного слоя вблизи поверхности шара (d@r/(Re)^1/2). При таких скоростях происходит ламинарное (слоистое) течение жидкости. Вне этого слоя реальная жидкость течет так же, как и идеальная, обтекая шар симметрично. Наоборот, при числах Re ~ 1 говорить о пограничном слое некорректно, т.к. градиенты скорости существенны в области, размеры которой значительно больше радиуса шара. При малых числах Рейнольдса сила лобового сопротивления для шара подчиняется закону Стокса: F_||=6pmrv. При Re>10², симметрия обтекания нарушается — позади шара происходит отрыв линий тока (рис. 4.22). При таких скоростях пограничный слой становится очень тонким, а поперечные градиенты скорости в нем — большими. Силы вязкости, которые при этом возрастают, тормозят движение частиц среды, движущихся вдоль поверхности шара, настолько, что они не в состоянии полностью обогнуть шар. Хотя течение в тонком пограничном слое остается ламинарным, позади шара образуются вихри. Симметрия давлений в точках А и A’ нарушается. F_||=C_X Srv²/2, где C_X — коэффициент лобового сопротивления для тела данной формы. Область квадратичной зависимости силы F от скорости v простирается вплоть до чисел Рейнольдса Re~10⁵. При больших скоростях пограничный слой постепенно турбулизуется, и при Re=3 10⁵ он полностью турбулентен. Для ламинарного и турбулентного обтекания тел можно использовать единую формулу для расчета силы лобового сопротивления: F_||=C_X(Re)Srv²/2, в которой коэффициент лобового сопротивления должен зависеть от скорости так, как это изображено на рис. 4.23.

 

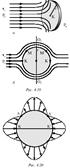
Взаимодействие тела с потоком идеальной жидкости. Еще Ньютоном была сформулирована получившая название ударной теория, базирующаяся на представлении воздуха в виде отдельных не связанных друг с другом материальных частиц. Согласно этой теории сила давления воздушного потока на площадку S, наклоненную под углом a (углом атаки) к направлению потока, равна: F=rSv²sin²a. Эта формула легко получается, если подсчитать импульс неупругих ударов составляющих ее материальных частиц. Опытная проверка этой формулы показала, что она неверно описывает зависимость силы F от угла атаки. И только при скоростях потока, значительно больших скорости звука, формула Ньютона оказывается справедливой. Модель воздуха как совокупности дискретных частиц является неверной. Реальные же силы могут быть подсчитаны на основе гидродинамического подхода, учитывающего обтекание тела движущимся потоком континуальной среды. Пусть в движущемся со скоростью v₀ потоке помещены диск и шар одинакового радиуса r (рис. 4.19). В центре диска точке K, называемой критической, поток останавливается (v = 0), и давление, согласно уравнению Бернули, равно: p_k=p₀+(rv₀²/2). Из-за поворота трубок тока на 90⁰ давление в других точках на поверхности диска будет таким же, как и в точке К. Поэтому, если позади диска давление равно p₀, то поток действует на диск с силой F_||=(p_k–p₀)pr²=rv₀²S/2. Гидродинамическая сила F, которая может трактоваться как сила лобового сопротивления при движении диска со скоростью v0 в потоке, вдвое меньше силы, вычисляемой на основе ударной теории ((1) при sin a=1). Если теперь в поток поместить шар, то по ударной теории на него будет действовать та же сила, что и на диск. При гидродинамическом подходе эта сила будет отсутствовать вовсе. Действительно, при симметричном потоке относительно сечения О₁ О₂ давления в произвольной точке М и симметричной точке M' будут одинаковы, поскольку одинаковы скорости потока в этих точках. Равенство нулю результирующей силы при плавном (безотрывном) обтекании идеальной жидкостью шара, цилиндра и другие. называется парадоксом Даламбера. Давление в любой точке потока вблизи поверхности шара можно рассчитать, пользуясь уравнением Бернулли: p_k=p₀+(rv₀²/2)–(rv²/2). На рис. 4.20 изображено распределение избыточных сил давления s_p=p–p₀, действующих по нормали к поверхности шара. Отсутствие сил в точках А и Aґ есть результат равенства скоростей в этих точках исходной скорости потока. При больших числах Рейнолдса сила лобового сопротивления обусловлена разностью давлений, а при малых – вязкостью.

Пункт 1. Момент импульса материальной точки. Пусть положение некоторой материальной тоски относительно точки О, принятой за начало координат, характеризуется радиусом-вектором r. Моментом импусльса материальной точки относительно О называется вектор L=r´p.

Моментом импульса системы материальных точек относительно тоски О, принятой за начало, называется сумма моментов импульса, материальных точек, составляющих систему.

Моментом силы F относительно точки O называется векторное произведение радиус-вектора r на силу F: M=[rF].

Момент силы относительно оси есть проекция на эту ось его момента относительно точки лежащей на той же оси.

Закон сохранения момента импульса. Этот закон справедлив лишь для изолированных систем. Для них момент внешних сил М равен нулю и уравнение моментов принимает вид dL/dt=0

Интегрируя это уравнение получаем L=const, L_x=const, _y=const, L_z=const Это равенство выразает закон сохранения момента импульса: момент импусльса изолированной системы не изменяется при любых процессах, происходящих внутри системы. Может случится, что система не является полностью изолированной, но на некоторое направление, например на ось z, проекция момента сил равна нулю. Тогда уравнение моментов озапишится в проециях в следующем виде: dL_x/dt=M, dL_y/dt=M, dL_z/dt=0. L_z=const. Поэтому закон сохранения момента импульса можно применять не только к полностью изолированным системам, но и к частичнро изолированным.

Билет № 11.

Работой силы F на перемещении ds называется проэкция Fs на направление перемещения, умноженная на само перемещение: dA = Fds = F*ds*cosx, где x – угол между векторами F и ds. Величина dA называется элементарной работой. Энергия системы – это запас ее работы. Кинетическая энергия – запаса работы системы которую она может совершить двигаясь до полной остановки. Потенциальная энергия – запас той работы системы которую она может совершить изменением своей конфигурации (взаимного расположения своих частей).

Пункт 2.

Подъемная сила – перпендикулярная составляющая силы действующей на тело со стороны потока.

Если неподвижный круглый цилиндр обтекается равномерным потоком воздуха, перпендикулярным к его оси, то вследствие симметрии возникает только лобовое сопротивление, но никакой подъемной силы не появляется. Если однако цилиндра привести во вращение, то появляется подъемная сила перпендикулярная к направлению внешнего потока, и цилиндр отклоняется в сторону. Это явление называется эффектом Магнуса.

Билет № 12.

Консервативными наз. силы, зависящие только от конфигурации системы, и работа которых по любому замкнутому контуру равна 0. Все силы, не являющиеся консервативными, называются неконсервативными. К ним относятся прежде всего диссипативные силы. Диссипативными называются такие силы, полная работа которых при любых движениях в замкнутой системе всегда отрицательна. Примером может служить сила трения или силы сопротивления в жидких и газообразных средах.

Какое-либо произвольное положение системы условно примем за нулевое. Работа, совершаемая конс. силами при переходе системы из рассматриваемого положения в нулевое, называется потенциальной энергией системы в первом положении. Потенциальная энергия при фиксированном нулевом положении зависит только от координат материальных точек системы. Иными словами, потенциальная энергия системы U является функцией только ее координат. В системе с одними только конс. силами полная энергия остается неизменной. Могут происходить только превращения энергий, но полный запас измениться не может (закон сохр. энергии).

Пункт 2.

Колебания – это повторяющееся движение. Число степеней свободы – это число независимых величин, которые необходимо задать для того, чтобы однозначно определить положение тела в пространстве.

Колебания с одной степенью свободы – это колебания при которых движения системы можно описать одним независимым параметром (координатой). Пример: колебания математического маятника, колебания физического маятника (твёрдое тело, подвешенное за точку и способное колебаться вокруг оси, не проходящей через ц. м.), колебания груза на пружинке. Колебания происходящие по закону sinуса или cosинуса наз. гармоническими. Собственными называются колебания системы под действием лишь внутренних сил без внешних воздействий.

Уравнение собственных незатухающих колебаний: x’’+vx’=0. Его решение: x=Asin(wt+j) или x=Bcos(wt+j). Величина A называется амплитудой, w -частотой, wt+j -фазой, j - начальной фазой.

Билет № 13.

Абсолютно неупругим ударом, называется столкновение двух тел, в результате которого они соединяются вместе и движутся дальше как одно тело.

Сталкивающиеся тела деформируются, возникают упругие силы и т.д. Однако если удар неупругий то, в конце концов все эти процессы прекращаются, и в дальнейшем оба тела, соединившись вместе, движутся как единое твёрдое тело.

v₁ v₂

m₁ m₂

Рассмотрим абс. неупругий удар на примере столкновения двух шаров. Пусть они движутся вдоль прямой, соединяющей их центры, со скоростями v₁ и v₂. В этом случае говорят что удар является центральным. Обозначим за V общую скорость шаров после соударения. Закон сохр. Импульса даёт:

m₁v₁+m₂v₂=(m₁+m₂)V Þ V=(m₁v₁+m₂v₂)/(m₁+m₂)

Кин. энергии системы до удара и после: K₁=1/2(m₁v₁²+m₂v₂²) K₂=1/2(m₁+m₂)V Пользуясь этими выраж. получаем: K₁-K₂=1/2m(v₁-v₂) ² где m =m₁m₂/(m₁+m₂) приведенная масса шаров. Таким образом, при столкновении двух абсолютно неупругих шаров происходит потеря кин. энергии макроскопического движения, равная половине произведения приведённой массы на квадрат относительной скорости.

Абсолютно упругим ударом называется столкновение тел, в результате которого их внутренние энергии не меняются. Пример: Столкновение бильярдных шаров из слоновой кости, при столкновениях атомных, ядерных частиц. Рассмотрим центральный удар двух шаров, движущ-ся навстречу друг другу:

(m₁v₁²)/2+(m₂ v₂²)/2=(m₁u₁²)/2+(m₂ u₂²)/2

и:

m₁v₁+m₂v₂=m₁u₁+m₂u₂

u1=[(m₁-m₂)v₁+2m₂v₂] / (m₁ +m₂)

u2=[(m₂-m₁)v₂+2m₁v₁] / (m₁+m₂)

При столкновении двух одинаковых абсолютно упругих шаров они просто обмениваются скоростями.

Пункт 2. см. предыдущий билет. Начальные условия: Гармоническое колебание полностью характеризуется частотой, амплитудой и начальной фазой.Частота зависит от физических свойств системы. Для определения амплитуды и начальной фазы колебаний надо знать положение и скорость материальной точки в некоторый момент времени.

Билет № 14.

Неинерциальные системы отсчёта (НИСО). НИСО называется система, движущаяся ускоренно относительно инерциальной. СО связана с телом отсчёта, которое, по определению, принимается за абсолютно твёрдое. Опр 2: в СО, в которых имеются силы тяготения и в к-х не выполняется 1-ый з-н Ньютона, наз. НИСО.

Описание движения мат. точки в НИСО. Чтобы описать движение в некоторой СО, необходимо разъяснить содержание высказывания о том, что такие-то события произошли в таких-то точках в такие-то моменты времени. Для этого надо, чтобы в СО $ единое время, но в НИСО единого времени в указанном §7 учебника Матвеева смысле не существует. Понятие длительности процессов, начинающихся в одной точке, а заканчивающихся в другой, теряет смысл, поскольку скорость хода часов в различных точках различна. Также трудно определить понятие длинны движущегося тела, если не ясно, что такое одновременность в различных точках. Эти трудности можно частично обойти, если принять во внимание, что интервал собственного времени не зависит от ускорения. Поэтому анализа пространственно-временных соотношений в некоторой бесконечно малой области НИСО можно воспользоваться пространственно-временными соотношениями ИСО, которая движется с той же скоростью, но без ускорения, как и соответствующая бесконечно малая область НИСО. Такая ИСО наз. сопровождающей. Рассмотрим движения с малыми скоростями, когда все эти трудности не возникают и можно использовать преобразования Галилея, считая, что пространственно-временные соотношения с НИСО таковы же, как если бы она была ИСО.

Силы инерции: переносная и кориолисова. В НИСО $ ускорения, которые не связаны с силами такого же характера, какие известны в ИСО. В НИСО, так же как и в инерциальных, ускорения вызываются силами, но наряду с «обычными» силами взаимодействия $ ещё и силы особой природы, называемые силами инерции. 2-ой з-н Ньютона формулируется без изменения, но наряду с силами взаимодействия необходимо учесть силы инерции. Силы инерции берутся такими, чтобы обеспечить в НИСО те условия, которые фактически имеются. 2-ой з-н Ньютона в НИСО: ma’=F+F_ин., где a’ – ускорение в НИСО, F – «обычные силы», F_ин – силы инерции. Переносная сила инерции направлена противоположно переносному ускорению НИСО и равна F_ин= – ma₀. Рассмотрим силы инерции во вращающейся СК:

F_ин=m(a’–a)=m(–a₀–a_K)=mw²R–2m[w v’]=F_цб+F_К. F_цб= mw²R – центробежная сила инерции. F_К=–2m[w v’] – сила инерции связанная с кориолисовым ускорением называется силой Кориолиса. Она перпендикулярна плоскости, в которой лежат векторы угловой и относительной скоростей. Если эти векторы колинеарны, то Кориолисово ускорение равно 0.

ентробежная и кориолисова силы инерции. Примеры проявления их действия.

Аабс=Аотн+2[w*Vотн]+dv0/dt+[w[wr]]+[dw/dt*r],2[w*Vотн]=Акор, [dw/dt*r]=Ацб, Fкор=-mАкор=2m[Vотн*w], Fцб=-[dw/dt*r]. Центробежные силы инерции существуют лишь в ускоренно движущихся (вращающихся) системах отсчета и исчезают при переходе к инерциальным системам. (Рассуждения на тему см. в Сивухине стр.374). бь

Примеры: пассажир в движ. транспорте на поворотах и т.п.

Кориолисова сила инерции возникает, когда матер. точка движется относительно вращающейся системы отсчета. От других сил инерции кориол. сила отличается тем, что она зависит от относительной скорости Vотн.

Пример: маятник Фуко, пассажир на повороте идет по автобусу и т.п.

Кориол. сила всегда перпендикулярна к относительной скорости, поэтому при относительном движении она не совершает работы. Следов., она является гироскопической силой (см. Сивухин, стр.145).

Пункт 2.

Сложение гармонических колебаний одинаковой частоты. x₁=A₁cos(wt+j₁), x₂=A₂cos(wt+j₂). Представим в комплексной форме: x=x₁+x₂=A₁e^i(wt+j1)+A₂e^i(wt+j2)=e^iwt(A₁e^ij1+A₂e^ij2), A₁e^ij1+A₂e^ij2=Ae^ij, A²=A₁²+A₂²+2A₁A₂cos(