чем отличие капельных жидкостей от твердых тел и газов?
В отличие от твердого тела жидкость характеризуется малым сцеплением между частицами, вследствие чего она обладает текучестью и принимает форму сосуда, в который ее помещают.
Жидкости подразделяют на два вида: капельные и газообразные. Капельные жидкости обладают большим сопротивлением сжатию (практически несжимаемы) и малым сопротивлением касательным и растягивающим усилиям (из-за незначительного сцепления частиц и малых сил трения между частицами). Газообразные жидкости характеризуются почти полным отсутствием сопротивления сжатию. К капельным жидкостям относятся вода, бензин, керосин, нефть, ртуть и другие, а к газообразным — все газы.
Гидравлика изучает капельные жидкости. При решении практических задач гидравлики часто пользуются понятием идеальной жидкости — несжимаемой среды, не обладающей внутренним трением между отдельными частицами.
К основным физическим свойствам жидкости относятся плотность, давление, сжимаемость, температурное расширение, вязкость.
Плотность — это отношение массы к объему, занимаемому этой массой. Плотность измеряют в системе СИ в килограммах на кубический метр (кг/м3). Плотность воды составляет 1000 кг/м3.
Используются также укрупненные показатели: – килопаскаль — 1 кПа= 103 Па; – мегапаскаль — 1 МПа = 106 Па.
Сжимаемость жидкости — это ее свойство изменять объем при изменении давления. Это свойство характеризуется коэффициентом объемного сжатия или сжимаемости, выражающим относительное уменьшение объема жидкости при увеличении давления на единицу площади. Для расчетов в области строительной гидравлики воду считают несжимаемой. В связи с этим при решении практических задач сжимаемостью жидкости обычно пренебрегают.
Величина, обратная коэффициенту объемного сжатия, называется модулем упругости. Модуль упругости измеряется в паскалях.
Температурное расширение жидкости при ее нагревании характеризуется коэффициентом температурного расширения, который показывает относительное увеличение объема жидкости при изменении температуры на 1 С.
В отличие от других тел объем воды при ее нагревании от 0 до 4 °С уменьшается. При 4 °С вода имеет наибольшую плотность и наибольший удельный вес; при дальнейшем нагревании ее объем увеличивается. Однако в расчетах многих сооружений при незначительных изменениях температуры воды и давления изменением этого коэффициента можно пренебречь.
Вязкость жидкости — ее свойство оказывать сопротивление относительному движению (сдвигу) частиц жидкости. Силы, возникающие в результате скольжения слоев жидкости, называют силами внутреннего трения, или силами вязкости.
Силы вязкости проявляются при движении реальной жидкости. Если жидкость находится в покое, то вязкость ее может быть принята равной нулю. С увеличением температуры вязкость жидкости быстро уменьшается; остается почти постоянной при изменении давления.
ак определяется равнодействующая сила гидростатического давления, действующего на криволинейную поверхность?
Схема к определению силы давления
на цилиндрическую поверхность АВ(2.8)
R – реакция стенки, равная равнодействующей сил давления на криволинейную поверхность S;
R x, R z – составляющие сил реакции по координатным осям, соответственно равные Р x и Р z;
S x, S z – площади горизонтальной и вертикальной проекций криволинейной поверхности АВ;
т. Д ´ – центр давления горизонтальной составляющей R x;
т. Д - центр давления равнодействующей сил гидростатического давления на поверхность АВ.
Равнодействующая сил давления R проходит через точку пересечения горизонтальной силы с вертикальной составляющей и центр окружности О (рис. 2.8). Координаты центра давления равнодействующей определяют следующим образом:
, (2.19)
откуда z = x · 
, (2.20)
Здесь x и z – соответственно горизонтальная и вертикальная координата центра давления, м.
Подставив значение z (2.20) в уравнение окружности:
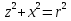(2.21)
получим следующее выражение:
, (2.22)
где r – радиус цилиндрической поверхности, м.
= P z/ P x (2.23)
определяют как отношение числовых значений составляющих сил давления, полученных их формул (2.18) и (2.17).
Таким образом, выполнив расчеты по формулам (2.17)…(2.23), находят значение горизонтальной и вертикальной координат центра давления, а также величину угла φ, равного
(2.24)
