Испытываются m элементов системы энергоснабжения самолета, которые работают независимо один от другого. Длительность времени безотказной работы элементов распределена по показательному закону с функциями надежности Ri(t), 
для каждого из 
элементов, где 
;
Определить вероятность того, что в интервале (0;β) часов откажут
а) только один элемент;
b) только два элемента;
c) только три элемента.
d) только четыре элемента;
i) все m элемента.
Дано:
m = 5; α1 = 0,33; α2 = 0,43; α3 = 0,13; α4 = 0,48; α5 = 0,53; β = 5;
Решение
атематическая часть
Введем обозначения:
– A1, A2, A3, A4, A5 – событие, состоящее в том, что отказал только один элемент, только два, три, четыре, все пять элементов, ни один элемент не отказал.
– p1, p2, p3,, p4, p5 – вероятность отказа 1-го, 2-го, 3-го,4-го,5-го элемента в заданном интервале (0;5) соответственно; тогда
– q1, q2, q3, q4, q5 – вероятность безотказной работы 1-го, 2-го, 3-го,4-го,5-го элемента в заданном интервале (0;5) соответственно;
Вероятность p1 отказа 1-го элемента в заданном интервале (0;5) будет равна:
, следовательно:
.
Вероятность p2 отказа 2-го элемента в заданном интервале (0;5) будет равна:
, следовательно:
.
Вероятность p3 отказа 3-го элемента в заданном интервале (0;5) будет равна:
, следовательно:
.
Вероятность p4 отказа 4-го элемента в заданном интервале (0;5) будет равна:
, следовательно:
Вероятность p5 отказа 5-го элемента в заданном интервале (0;5) будет равна:
, следовательно:
.
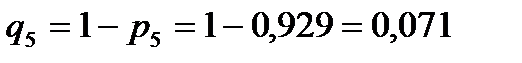асчетная часть
Переходим к расчету искомых вероятностей, которые находится следующим образом:
Вероятность 
отказа только одного элемента в заданном интервале (0;5) будет равна:
Вероятность 
отказа только двух элементов в заданном интервале (0;5) будет равна:
Вероятность 
отказа только трех элементов в заданном интервале (0;5) будет равна: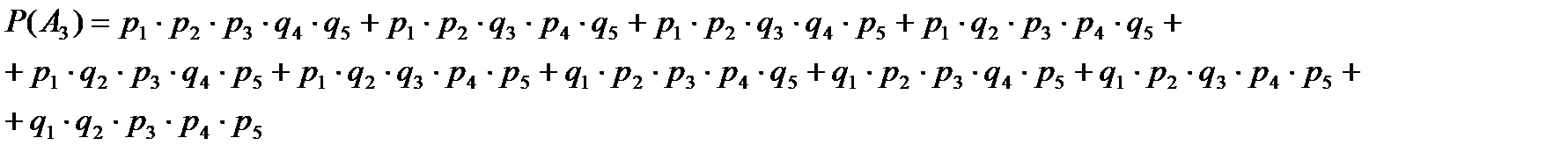 
Вероятность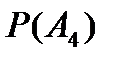 
отказа только четырех элементов в заданном интервале (0;5) будет равна:
Вероятность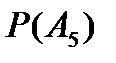 
отказа всех пяти элементов в заданном интервале (0;5) будет равна:
Вероятность 
безотказной работы всех пяти элементов за время испытания в заданном интервале (0;5) будет равна:
.
Вывод
На основании изложенного можно заключить, что при заданных данных во время испытаний в заданном интервале (0;5) наиболее вероятным являются отказ только четырех элементов, а наименее вероятным является отказ одного элемента, так как:
Вероятность того, что все пять элементов безотказно отработают во время испытаний в заданном интервале (0;5) является небольшой, а именно:
.
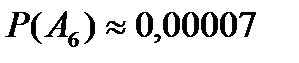Приложение:
1. Теорема сложения вероятностей.
Вероятность суммы конечного числа несовместных событий равна сумме вероятностей этих событий, т. е.
,
где 
= Ø при 
.
Если события A1, A2,…, 
образуют полную группу несовместных событий, то 
. В частности, события 
и 
образуют полную группу и несовместны, поэтому 
. Если обозначить 
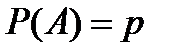, то 
.
2. Теорема умножения вероятностей.
Вероятность произведения конечного числа событий равна произведению вероятности одного из них и условных вероятностей остальных событий, вычисленных при условии, что все предшествующие события произошли, т. е.
… 
.
События 
и 
называются независимыми, если 
. Тогда 
, т.е. независимость событий взаимная. События A1, A2,…,
называются независимыми в совокупности, если каждое из них и любые комбинации их совместной реализации являются независимыми событиями. Для независимой в совокупности системы событий 
справедливо равенство
.
Если любые два события системы независимы, то система событий называется попарно независимой.
Список использованных источников:
1. А. П. Рябушко «Индивидуальные задания по высшей математике» 4-е издание, «Высшая школа», 2007.
2. «Авиация: Энциклопедия» М.: Большая Российская энциклопедия, 1994 г.
3. Е.С. Вентцель, Л.А. Овчаров «Теория вероятностей и её инженерные приложения» 4-е издание, «Высшая школа», 2007 г.
4. Интернет источник http://dic.academic.ru/dic.nsf/enc_tech/2812.
