атематическая часть задания 1

равнительный анализ вероятностей катастрофы летательного аппарата

 

остановка задачи задания №1

Задание 1

 

Летательный аппарат (ЛА) состоит из

- m двигателей с вероятностей отказа Р₁ Р₂,...Р_т;

- п дублирующих систем энергоснабжения с вероятностей отказа Р_1Э, Р_2Э,...Р_nэ;

- N с вероятностей отказа Р_с каждая.

Катастрофа наступает, если выходит из строя любая (R+1) и более двигателей, либо если все системы энергоснабжения, либо если хотя бы одна из N вспомогательных подсистем.

В случае отказа любого r из m двигателей катастрофа наступает с вероятностью Р_D;

Определить вероятность катастрофы ЛА и сравнить ее с вероятностью катастрофы ЛА без дублирующих систем (один двигатель с вероятностью катастрофы Р₁, одна система энергоснабжения с вероятностей отказа Р_1Э и N вспомогательных подсистем с вероятностей отказа Р_с каждая), предполагая, что все упомянутые выше системы и подсистемы ЛА функционируют независимо друг от друга.

В обоих случаях сравнить вероятности катастроф, связанных с отказом

- двигателей;

- систем энергоснабжения;

- вспомогательных подсистем.

 

 

Дано:

m = 3; Р₁ =8∙10^-4, Р₂ =2∙10^-4, Р₃=4∙10^-4

r=2; Р_D=0,6;

n=3; Р_1Э=5∙10^-3, Р_2Э=4∙10^-4, Р_3Э=10 ^-3;

N=10³; P_c=3∙10^-8.

Решение

атематическая часть задания 1

 

Введем обозначение событий:

- D₁, D₂, D₃ - отказ 1-го, 2-го, 3-го двигателей соответственно;

- В₁, В₂, В₃, - отказ 1-й, 2-й, и 3-й системы энергоснабжения соответственно;

- С_i - отказ i- ой вспомогательной подсистемы, i=1, 2,...,N;

- Е_к - катастрофа;

-E_kd, E_кэ , E_кc - катастрофы, связанные с отказом двигателей, систем энергоснабжения и вспомогательных подсистем соответственно.

 

А)Рассмотрим случай ЛАс дублирующими системами:

В этом случае:

Е_K=Е_KD+Е_KЭ+E_КС. (1.1)

Перейдем к противоположным событиям, будем иметь:

 

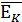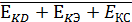= . (1.2)

Из равенства (1.2) в силу соотношения двойственности получим:

 

Е_K= 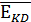∙ ∙ 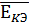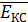. (1.3)

 

Тогда вероятность катастрофы будет определяться по формуле:

P(E_K)=1- P(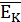)=1-P( 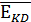∙ ∙ 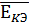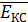). (1.4)

Из равенства (1.4) в силу независимости событий Е_KD,Е_KЭ, E_КС получим:

 

P(E_K)=1- P ∙ P()∙ P(E_KC)=1-(1-P(E_KD))∙(1-P(E_KЭ))∙P(E_KC)). (1.5)

Рассмотрим структуру событий Е_KD, Е_KЭ, E_КС и найдем их вероятности, то есть вероятности катастроф, связанных с отказом:

- двигателей Е_КD;

- систем энергоснабжения Е_KЭ;

- вспомогательных подсистем Е_KC.

 

1) Рассмотрим структуру событий Е_KDи найдем P(E_KD)= P_KD.

 

Так как событие Е_KD - это событие, состоящее в том, что катастрофа произошла из-за отказа двигателей, а по условию задачи катастрофа, связанная с отказом двигателей наступает, если выходят из строя любых (r+1) и более двигателей из m двигателей, а в случае отказа любого r из m двигателей катастрофа наступает с вероятностью Р_D. Значит:

 

Е_KD= Е_KDr+ Е_KD(r+1), где

Так как в нашем случае число двигателей m = 3, r = 2; то r + 1 = 2 + 1 = 3.

Значит:

 

Е_KD= Е_KD2+ Е_KD≥3, где

Е_КD2 - событие, состоящее в том, что катастрофа произошла из-за отказа любого r =2 из m=3 двигателей;

Е_KD≥3 - событие, состоящее в том, что катастрофа произошла из-за выходы из строя любых (r+ 1) = 3 и более двигателей, а в нашем Е_KD≥3= Е_KD3 - это событие, состоящее в том, что катастрофа произошла из-за отказа трех двигателей. Из этого следует, что:

 

Е_KD≥3= Е_KD3=D₁∙ D₂∙ D_3. (1.6)

В свою очередь катастрофа, связанная с отказом ровно r = 2 двигателей (при работающих остальных), не обязательно влечет за собой катастрофу (ас вероятностью P_D), значит E_KD2=E_K∙ E_D2.

Тогда:

E_KD= E_KD2+ E_KD3= E_K∙ E_D2+ E_KD3.

Так как события E_KD2, и E_KD≥3 несовместны, то

P(E_KD)=P(E_KD2+ E_KD3)=P(E_KD2)+ P(E_KD3)=P(E_K∙ E_D2)+P(E_KD3).

а для нашего случая и учитывая (1.6), получим:

P(E_KD)=P(E_KD2+ E_KD≥3)=P(E_KD2)+ P(E_KD3)=P(E_K∙ E_D2)+P(E_KD3)=

=P(E_K∙ E_D2)+P(E_KD3)= P(E_K∙ E_D2)+ P(D₁∙ D₂∙ D₃).

С другой стороны, катастрофа, связанная с отказом ровно r=2 двигателей при работающих остальных из трех имеющихся у ЛА по условию задачи, есть следующее событие:

E_D2 = D₁∙ D₂ 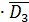+D₁∙ ∙ D₃+ ∙ D₂ ∙ D_3.. (1.8)

то есть не работают 3-й, 2-й,1-й двигатели из трех, имеющихся у ЛА.

 

Тот факт, что события E_KD2 и E_KD3 несовместны, можно доказать следующим образом:

E_KD2 ∙ E_KD3 =<согласно(1.7) >= E_K∙ E_D2 ∙ E_KD3 =<согласно(1.6) >= E_K∙ E_D2 ∙Е_KD3= =<согласно(1.6) и(1.8) >= E_K(D₁∙ D₂ 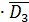+D₁∙ ∙ D₃+ ∙ D₂ ∙ D₃)∙ D₁∙ D₂∙D₃=

=E_K((D₁∙ D₂ 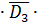D₁∙ D₂∙ D₃)+(D₁∙ ∙ D₃∙ D₁∙ D₂∙ D₃)+( ∙ D₂ ∙ D₃ ∙ D₁∙ D₂∙ D₃)=

=E_K((D₁∙ D₁)∙(D₂ ∙D₂)∙(D₃∙ 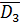) + (D₁∙ D₁)∙(D₂∙ ∙)∙(D₃∙ D₃)+

+(D₁∙ )∙(D₂∙ D₂)∙(D₃∙ D₃).

Используя тот факт, что A∙A =A и A∙ 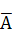=Ø, получим

E_KD2∙ E_KD≥3 =E_K((D₁ ∙D₂ ∙ Ø) + (D₁ ∙Ø∙D₃)+(Ø ∙D₂ ∙D₃))=Ø.

А как известно, что, если произведение двух событий равно невозможному событию (пустому множеству), то такие события являются несовместными.

По определению условной вероятности имеем:

P(E_KD)=P(E_K / E_D2)∙P(E_D2)+P( ).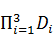

а в силу независимости событий D_i, i= 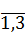, далее имеем:

P(E_K / E_D2) ∙ P(E_D2)+ P( ).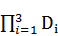

Используя (1.7) и несовместимость его (E_D2) слагаемых

P(E_K / E_D2)∙( P(D₁∙ D₂ ∙ 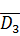)+P(D₁∙ 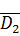∙ D₃)+ P( 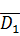∙ D₂ ∙ D₃))+ ).

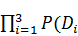В силу всех независимых событий D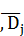_i , i= 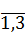и потому, что

P(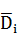)=1-P(D_i), получим далее:

P(E_K / E_D2)∙[P( D₁ )∙P( D₂ )∙(1-P( D₃ ))+P( D₁ )∙(1-P( D₂ ))∙P( D₃ )+

+(1-P( D₁ )∙P( D₂ )∙P( D₃ )]+ ).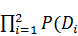

Так как P(D_i)=P_i, i= 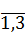и P(E_K / E_D2)=P_D, имеем

P(E_KD)=P_D∙[ P₁∙ P₂∙(1- P₃)+P₁∙(1-P₂)∙P₃ +(1- P₁)∙P₂∙P₃]+P₁∙P₂∙ P₃=

= P_D∙[P₁∙ P₂+P₁∙ P₃+ P₂∙ P₃]∙(1-3P_D)∙ P₁∙ P₂∙ P₃≡P_KD. (1.9)

Если выполняется условие P«P_D для всех i= 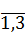и учитывая, то что значение вероятности случайного события есть величина, меньшая единицы, то:

P₁∙ P₂∙ P₃ →0

А значит тоже:

(1-3P_D)∙ P₁∙ P₂∙ P₃→0

И тогда имеем:

P(E_KD)≡P_KD≈ P_D∙(P₁∙ P₂+ P₁∙ P₃+ P₂∙ P₃). (1.10)

Подставив значения, данные из условия задания, получим:

P(E_KD)≡P_KD≈P_D ∙(P₁∙ P₂+ P₁∙ P₃+ P₂∙ P₃)=

=0.6∙(8∙10^-4∙2∙10^-4+8∙10^-4∙4∙10^-4+2∙10^-4∙4∙10^-4)=

=0.6∙10^-8∙(16+32+8)=33,6∙10^-8. (1.11)

2) Рассмотрим структуру событий Е_кэи найдем P(E_КЭ)=P_КЭ

E_КЭ≡ B₁∙ B₂∙ B₃- катастрофа, связанная с отказом всех трех систем энергоснабжения (n= 3 по условию задачи).

 

В силу независимости всех событий B_i, i= 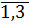имеем

P(E_КЭ) ≡P(B₁∙B₂∙B₃)=P(B₁) ∙P(B₂) ∙P(B₃)=P_1э∙P_2э∙P_3э. (1.12)

 

Подставив значения, данные из условия задания, получим

P(E_КЭ)≡P(B₁∙B₂∙B₃∙)=P(B₁) ∙P(B₂) ∙P(B₃)=P_1э∙P_2э∙P_3э=

= 5∙10^-4∙4∙10^-4∙10^-3=2∙10^-10. (1.13)

3) Рассмотрим структуру событий е_кс и найдем P(е_кс) = P_кс.

Событие Е_кс наступает, если отказывает хотя бы одна из вспомогательной подсистемы, значит

е_кс ≡C₁+C₂+…+C_N= .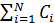

В силу закона двойственности

е_кс ≡ = ∙ ∙…∙ = .

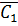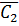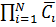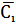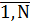в силу независимости событий , i= получим

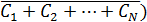P () ≡P( =P( ) ∙ P( 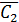)∙…∙ P( 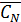)= = 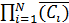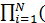1-P(C_i)).

 

Так как P(C_i)=P_{c ,} i= 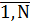получим

P (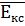)= = 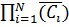1-P_с)=(1-P_c)^N.

тогда

P(е_кс)=(1- P (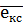)=1-(1-P_c)^N ≡P_KC.

Если выполняется NP_C<<1=>

P ()=(1-P_c)^N=1-NP_C+ 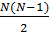P_C²-…(-1)^NP_c^N≈ 1-NP_C. (1.14)

Подставив значения, данные из условия задания, получим

P(е_кс) 1-1+NP_C=NP_C=10³∙3∙10^-8=3∙10^-5. (1.15)

асчетная часть

Переходим к числовым расчетам. Вычислим вероятность катастрофы по выведенной нами формуле (1.5). Так как в нашем случае выполняется условие (1.9), то

 

P(E_К)=1-(1-P(E_KD))∙(1-P (е_кс))∙P())=1- =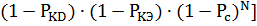

=1- 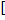1- P_D∙(P₁∙ P₂+ P₁∙ P₃+ P₂∙ P₃) + (1-3 )P₁P₂P₃) 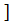∙(1-P_1Э∙ P_2Э∙ P_3ЭP_4Э)∙(1-P_c)^N.

Если выполняется условие NP_C<<1 и P­_KD<<1 и P_КЭ<<1, то будем далее иметь

P­_KD+ P_КЭ+ NP_C= 3,36∙10^-7 +2∙10^-10+ 3∙10^-5 ≈ 3∙10^-5.

Так как P­_KD=33 ,6∙10^-8; P_КЭ= 2∙10^-10; NP_C=3∙10^-5 =>

2∙10^-10≤ 3,3 6∙10^-7≤ 3∙10^-5, из этого видно, что P_КЭ ≤ P_KD≤ P _ксиз этого следует, что вероятность катастрофы, связанной с отказом вспомогательных подсистем, является определяющей.

 

В) Теперь рассмотрим случай ЛА без дублирующих систем:

 

Р₁=8∙10^-4, Р_1Э=5∙10^-4, N=10³, P_c=3∙10^-8=>

P’(E_K)=P₁+P_1Э+NP_C=8∙10^-4+5∙10^-4+3∙10^-5 = 13,3∙10^-4.

2 ∙10^-10 < 3 ∙10^-8 <8 ∙10^-4, из этого видно что P_КЭ< P’_КС < P’_KD, а из этого следует, что вероятность катастрофы, связанной с отказом двигателя и вспомогательных систем, является определяющей.

И, наконец, сравним вероятности P’(E_K) и P(E_K):

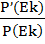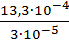= =44,3(раза).

Вывод

 

На основании вышеизложенного можно заключить, что наиболее вероятной является катастрофа, связанной с отказом одной из вспомогательных подсистем, а отсутствие дублирующих систем увеличивает вероятность катастрофы в 44,3 раза, при этом определяющим фактором становится отказ двигателя или системы энергоснабжения. В данном случае при m=3, а r=2, отсутствие дублирующих систем существенно увеличивает вероятность катастрофы.

 

адание 2