омплексные числа.
Пример 1. Построим на комплексной плоскости следующие комплексные числа:
, 
, 
, 
, 
, 
, 
, 
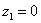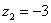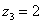
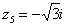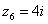
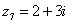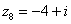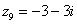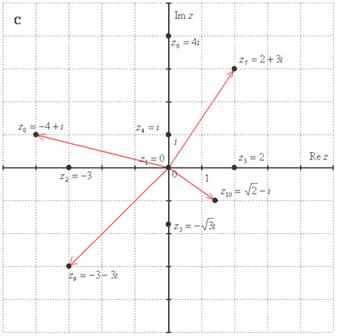
Числа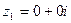 
, 
, 
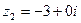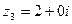– комплексные числа с нулевой мнимой частью.
Числа 
, 
, 
, – это, наоборот, чисто мнимые числа, т.е. числа с нулевой действительной частью. Они располагаются строго на мнимой оси 
.
В числах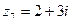 
, 
, 
, 
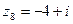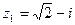и действительная и мнимая части не равны нулю. Такие числа тоже обозначаются точками на комплексной плоскости, при этом, к ним принято проводить радиус-векторы из начала координат (обозначены красным цветом на чертеже). Радиус-векторы к числам, которые располагаются на осях, обычно не чертят, потому, что они сливаются с осями.
ложение комплексных чисел.
Пример 2.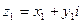 
и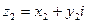 
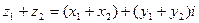
Сложить два комплексных числа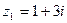 
, 
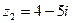
Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:
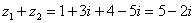
Пример 3. Вычитание комплексных чисел. 
Найти разности комплексных чисел: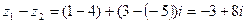 
множение комплексных чисел.
· 
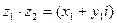Пример 4. Найти произведение комплексных чисел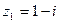 
, 
Необходимо раскрыть скобки по правилу умножения многочленов, главное, помнить, что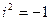 
.
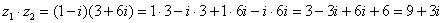
Понятно, что 
ример 5. Деление комплексных чисел.
Даны комплексные числа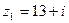 
, 
. Найти частное.
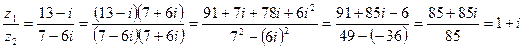
Пример 6.1. Представить в тригонометрической форме число 
. Найдем его модуль и аргумент. 
.
Очевидно, что 
(число лежит непосредственно на действительной положительной полуоси). Таким образом, число в тригонометрической форме: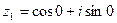 
.
Обратное проверочное действие: 
Пример 6.2. Представить в тригонометрической форме число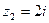 
. Найдем его модуль и аргумент. 
. 
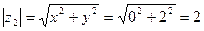Таким образом, число в тригонометрической форме: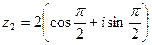 
.
Используя таблицу значений тригонометрических функций, легко обратно получить алгебраическую форму числа (заодно выполнив проверку):
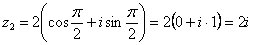
Пример 6.3. Представить в тригонометрической форме число 
. Найдем его модуль и аргумент.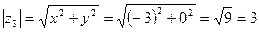 
Очевидно, что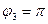 
(или 180 градусов). Таким образом, число в тригонометрической форме: 
.
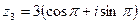Проверка: 
Пример 6.4. Представить в тригонометрической форме число 
.
Найдем его модуль и аргумент.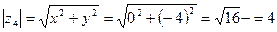 
,
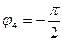(-90 градусов), и, соответственно: 
.
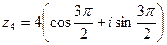Рассмотрим более распространенные случаи.
Модуль вычисляется по формуле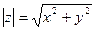 
. А вот формулы для нахождения аргумента будут разными, это зависит от того, в какой координатной четверти лежит число 
. При этом возможны три варианта:
1) Если 
> 0 (1-я и 4-я координатные четверти, или правая полуплоскость), то аргумент нужно находить по формуле 
.
2) Если x < 0, y > 0 (2-я координатная четверть), то аргумент нужно находить по формуле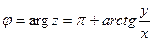 
.
3) Если x < 0, y < 0 (3-я координатная четверть), то аргумент нужно находить по формуле 
.
Пример 6.5. Представим в тригонометрической форме число 
. Найдем его модуль и аргумент. 
, 
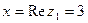, x >0, y > 0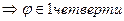 
. 
, 
Следовательно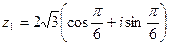 
Пример 6.6. Представим в тригонометрической форме число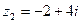 
. Найдем его модуль и аргумент. 
, 
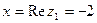x < 0, y > 0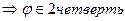 
.
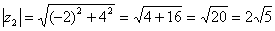
Следовательно 
Пример 6.7. Представим в тригонометрической форме число 
. Найдем его модуль и аргумент.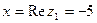 
, 
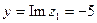, x <0, y < 0 
. 
, 
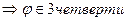Следовательно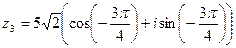 
Пример 6.8. Представим в тригонометрической форме число 
. Найдем его модуль и аргумент. 
, 
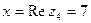, x >0, y < 0 
. 
, 
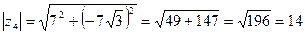Следовательно 
