Частотная характеристика
(1.25)
В записи (1.25) ЧХ формально представляет собой отношение двух комплексных чисел числителя и знаменателя.
Считая (1.25) показательной формой записи ЧХ, вычисляем АЧХ и ФЧХ:
- АЧХ: 
(1.26)
- ФЧХ: 
(1.27)
ВЧХ и МЧХ рассчитываем, используя дополнительное умножение числителя и знаменателя ЧХ на комплексно-сопряженное к знаменателю число:
откуда
(1.28)
Как видно, вывод выражений A (ɷ), W(j ɷ ), P (ɷ)и Q (ɷ)принципиально прост. Сложным являются вычисления координат точек годографа ЧХ, если принять во внимание, что при этих вычислениях нужно знать:
- до какого значения аргумента ɷ нужно считать (полный интервал изменения ɷот 0 до ¥)?;
- и каким должен быть шаг j ɷвычислений?
В сравнении с расчётами переходных процессов расчёты ЧХ сложнее тем, что нет простых процедур определения конечной (верхней) частоты ɷсчёта и шага j ɷ. Последний, к тому же, будет неравномерным.
Здесь следует пользоваться проверенными на практике приёмами расчёта ЧХ:
1. Необходимо предугадать вчерне вид годографа, а именно, где его начало и конец, через какие квадранты комплексной плоскости и в каком порядке он пройдёт при изменении частоты ɷот 0 до ¥.
Прежде всего, находят точки пересечения годографа с осями координат. Для этого решают уравнения:
P (w) =0 Þ -w4+2w2+9=0 Þ w=2,04, т.е. годограф пересекает мнимую ось на частоте w5=2,04, если в качестве иллюстрации расчётов принять рис.1.7;
Q (w) =0 Þ w(0,5w2+1,5) =0 Þ w=0, т.е. годограф пересекает действительную (вещественную) ось на частоте w1=0.
Далее вычисляют значения P (ɷ)и Q (j ɷ)при найденных частотах и на бесконечности при ɷ =¥.
2. Определяют значение угла j (¥), с которым годограф входит в начало координат, по формуле
j (¥) =-90o (n-m), (1.29)
где n и m - степени полиномов p, соответственно, знаменателя и числителя передаточной функции.
По результатам описанных вычислений строится в черновом варианте годограф ЧХ (рис.1.7).
3. Подготавливается таблица вычислений, состоящая из 5-ти строк (табл.1.4).
Таблица 1.4
| w | w 1=0 | w 2 | w 3 | w 4=2,04 | w 5 | w 6 | w 7 | w =¥ |
| P (w) | 0 | 0 | ||||||
| Q (w) | 0 | 0 | ||||||
| A (w) | 0 | |||||||
| (j w) | 0 | -90o | -180o |
В этой таблице прежде всего нужно заполнить первую строку - строку частот w. Все остальные строки затем заполнятся вычислениями по формулам (1.26)...(1.28).
Сначала находим частоты w2 и w3 для точек годографа, лежащих в 4-м квадранте. Очевидно, что эти частоты должны быть такими, чтобы точки годографа на этих частотах равномерно заполняли бы участок в 4-м квадранте, т.е. угол j между соседними точками был примерно равен 30о (ни в коем случае не надо стремиться получить точно 30о, а лучше задать, например, 30о 
10о). Руководствуясь этими соображениями, задаёмся частотой в пределах от 0 до 2,04 (эти значения верны только для рассматриваемого числового примера!) и вычисляем угол j. Если он равен 30о10о, то нами найдена (точнее - угадана) частота w2. Если вычисления дали 60о10о, то найдена частота w3. Иначе нужно снова задать значение w. Аналогично определяют частоты w5...w7 для 3-го квадранта.
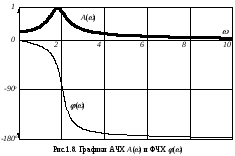
После заполнения строки частот заполняется значениями вся таблица. По значениям P (w) и Q (w строится годограф) W (wj)(рис.1.7), а по значениям A (w)и j (w)строятся АЧХ и ФЧХ (рис.1.8).
Замечание к расчётам по формуле (4.7) значений угла j на калькуляторе, компьютере и по таблицам тригонометрических функций. Во всех перечисленных случаях определяется только главные значения арктангенса - ARCTG (*), - которые находятся в пределах от -90о до +90о. Действительное значение угла определяется с учётом структуры выражения, находящегося под знаком arctg, которое является отношением мнимой Q к действительной P части соответствующего комплексного числа. Если P>0, то угол лежит в 1-м или 4-м квадрантах, если P<0, то угол лежит во 2-м или 3-м квадрантах. При Р=0 угол равен 90о:
где sign (Q)- знак числа Q.
Как видно из приведенных выше приёмов расчёта ЧХ такой расчёт содержит достаточно громоздкие вычисления.
