Экзаменационный билет № 6
По дисциплине «Математические основы теории автоматического управления»
1. Постановка задачи синтеза одноканальных систем. Модальный метод синтеза.
2. Частотные характеристики линейных САУ.
3. Задача.
Проверить устойчивость системы с помощью критерия Михайлова 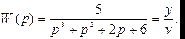
Постановка задачи синтеза одноканальных систем. Модальный метод синтеза.
- Обсудим содержание задачи синтеза для объекта, поведение которого описывается передаточной функцией
 (6.3)
(6.3)
с ограниченным ресурсом управления, 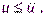 Влияние окружающей среды отражает возмущение M (t), а выходная переменная измеряется датчиком
Влияние окружающей среды отражает возмущение M (t), а выходная переменная измеряется датчиком

(первичным измерительным
преобразователем, сенсором) с помехой измерения h (t),
 = y + h(t).
= y + h(t).
Здесь - оценка выходной переменой у. На рис.6.3 представлена схема такого объекта, где пунктиром выделен Рис. 6.3. Структурная схема объекта датчик.
Целью функционирования замкнутой системы регулирования является организация свойства:
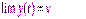 при
при  (6.4)
(6.4)
с заданной точностью 
Наряду с условием статики (6.4) предъявляются требования и к динамике, то есть к характеру переходных процессов, в виде оценок
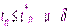 %
% 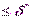 %. (6.5)
%. (6.5)
что представляет собой основную сложность расчета.
Необходимо определить структуру и параметры регулятора, обеспечивающего выполнение требований (6.4) и (6.5) в условиях действия возмущений и помехи измерения.
Заметим, что единственной величиной, которую можно использовать для организации управляющего воздействия u, является полученная с помощью датчика оценка выходной величины 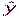 . Поэтому в лучшем случае в системе с заданной точностью
. Поэтому в лучшем случае в системе с заданной точностью 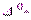 можно обеспечить выполнение свойства
можно обеспечить выполнение свойства
 при
при 
а не условия (6.4). Таким образом, при выборе измерительного устройства следует придерживаться рекомендаций:
- 1) датчик должен обладать точностью не меньшей, чем требуемая точность системы в целом;
- 2) нужно отфильтровывать помеху, частотный состав которой отличается от рабочих частот системы.
Ошибка регулирования представляет собой сумму трех составляющих
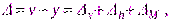
одна из которых 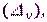 порожденная входным воздействием, может быть легко скомпенсирована с помощью масштабирования (см. раздел 3). Помеха h(t) высокочастотная, поэтому она проявляется в динамике, а в статике ее можно не учитывать
порожденная входным воздействием, может быть легко скомпенсирована с помощью масштабирования (см. раздел 3). Помеха h(t) высокочастотная, поэтому она проявляется в динамике, а в статике ее можно не учитывать 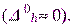
Следовательно, при синтезе необходимо обеспечить не более заданной статическую ошибку, порожденную возмущением, 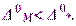
Модальный метод
Метод применяется для расчета систем, работающих в режиме отработки начальных условий. При этом математическая модель объекта управления записывается в форме:
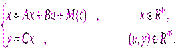 (6.41)
(6.41)
Требования к поведению замкнутой системы формулируются в виде условия статики (6.4):
lim y(t) = v при t  с точностью
с точностью 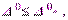
и оценок переходных процессов типа (6.5): 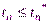 и %
и %  %, от которых переходят к желаемому распределению корней на комплексной плоскости. Так как корни являются модальным характеристикам системы, то и метод синтеза называется “модальным”.
%, от которых переходят к желаемому распределению корней на комплексной плоскости. Так как корни являются модальным характеристикам системы, то и метод синтеза называется “модальным”.
Структура регулятора предполагается известной, он описывается уравнением:
u = K x, (6.42)
где K - матрица неизвестных коэффициентов. Их необходимо определить таким образом, чтобы качество работы замкнутой системы, уравнения которой получают в результате подстановки (6.42) в (6.41),
 (6.43)
(6.43)
соответствовало заданному. С этой целью записывают ее характеристическое уравнение,
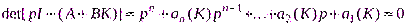 . (6.44)
. (6.44)
От заданного распределения корней переходят к желаемому характеристическому уравнению замкнутой системы:
 . (6.45)
. (6.45)
Приравнивая коэффициенты при соответствующих степенях p уравнений (6.44) и (6.45), получают соотношения для расчета элементов матрицы K в виде:
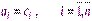 . (6.46)
. (6.46)
В общем случае зависимость 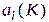 может быть нелинейной, поэтому найти K по выражению (6.46) не всегда удается даже для одноканального объекта, уравнения которого предварительно записывают в канонической форме.
может быть нелинейной, поэтому найти K по выражению (6.46) не всегда удается даже для одноканального объекта, уравнения которого предварительно записывают в канонической форме.
Поскольку одноканальный объект удобнее описывать с помощью передаточной функции, обсудим соответствующую методику модального метода синтеза.
Частотные характеристики линейных САУ.
Частотные характеристики линейных САУ рассчитываются через передаточные функции: если W (p) – передаточная функция, то W (j)– частотная характеристика (ЧХ), получаемая из передаточной функции путём замены в ней p на j ЧХ как комплексное число может быть представлено в показательной и алгебраической формах.
Показательная форма:
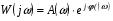 (1.22)
(1.22)
Эта запись позволяет найти еще две важнейшие характеристики: АЧХ и ФЧХ:
A (ω) – амплитудо-частотная характеристика (АЧХ);
W (jω) – фазо-частотная характеристика (ФЧХ).
Алгебраическая форма:
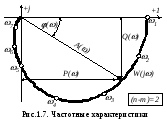 W(j) =P () +jQ (w) (1.23)
W(j) =P () +jQ (w) (1.23)
Данное выражение порождает еще две характеристики: 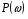 – вещественно-частотная характеристика (ВЧХ) и
– вещественно-частотная характеристика (ВЧХ) и  – мнимо-частотная характеристика (МЧХ).
– мнимо-частотная характеристика (МЧХ).
График ЧХ на комплексной плоскости называется годографом (рис.1.7).
Между величинами A, ᵠ, P и Q существуют связи (аргумент ɷопущен):
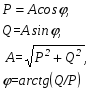 (1.24)
(1.24)
Особенности вычислений ЧХ можно проследить только на числовом
Примере 3.3.






