Методика Ишлинского
Методика составления уравнений движения СП,
установленных на подвижном основании
Уравнения движения гироскопических устройств, находящихся на неподвижном основании, обычно составляют, используя уравнение Лагранжа второго рода. В него входят кинетическая энергия системы; обобщенные силы, приложенные к системе; обобщенные координаты. В качестве обобщенных координат берутся углы поворотов подвеса, а обобщенных сил – вращающие моменты. Таким образом составляются уравнения движения одно-, двух- и трехосных платформ.
В случае многоосной платформы, установленной на движущемся основании, обобщенными координатами выступают углы Эйлера между осями платформы  и базовыми осями
и базовыми осями  . Объект поворачивается вокруг нематериальных осей, не совпадающих с осями подвеса. Задача становится трудной, и для ее решения применяется малодоступный метод виртуальных перемещений.
. Объект поворачивается вокруг нематериальных осей, не совпадающих с осями подвеса. Задача становится трудной, и для ее решения применяется малодоступный метод виртуальных перемещений.
 Более предпочтителен метод, основанный на теореме об изменении главного момента количества движения динамической системы. Его использовали Е. Л. Николаи и др., а развил применительно к сложным гироскопическим системам А. Ю. Ишлинский [1].
Более предпочтителен метод, основанный на теореме об изменении главного момента количества движения динамической системы. Его использовали Е. Л. Николаи и др., а развил применительно к сложным гироскопическим системам А. Ю. Ишлинский [1].
Рассмотрим указанный метод на примере составления уравнений движения одноосной силовой СП, представленной на рис. 2.1. Платформа состоит из ротора гироскопа, кожуха гироскопа, платформы и ротора стабилизирующего двигателя (СД). При использовании этого метода система рассматривается как совокупность твердых тел, сочлененных между собой связями (декомпозиция системы на элементы). На каждое тело действуют не только силы, но и реакции связей (опор и т. д.). С каждым из тел связаны оси: с ротором гироскопа – 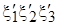 ; с кожухом –
; с кожухом –  ; с платформой –
; с платформой –  ; с ротором СД –
; с ротором СД – 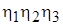 ; с объектом, на котором установлена СП, –
; с объектом, на котором установлена СП, –  . При этом ось
. При этом ось  , совпадающая с осью
, совпадающая с осью  , является осью вращения ротора; ось
, является осью вращения ротора; ось  , совпадающая с осью
, совпадающая с осью  , – осью вращения кожуха; ось
, – осью вращения кожуха; ось  , совпадающая с осью
, совпадающая с осью  , – осью вращения платформы; ось
, – осью вращения платформы; ось  , параллельная оси
, параллельная оси  объекта, – осью вращения ротора двигателя.
объекта, – осью вращения ротора двигателя.
На рис. 2.2 показаны тела, входящие в состав СП; связанные с ними системы координат и реакции опор (связей)  ,
,  . Реакции опор лежат в плоскости, перпендикулярной оси вращения тела. В соответствии с законом о силах действия и противодействия:
. Реакции опор лежат в плоскости, перпендикулярной оси вращения тела. В соответствии с законом о силах действия и противодействия:  . На рис. 2.2. реакции
. На рис. 2.2. реакции 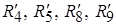 не указаны, так как соответствующие тела связаны с объектом.
не указаны, так как соответствующие тела связаны с объектом.

Рис. 2.2
Данная методика приводит к упрощению громоздких вычислений, при этом легко просматривается физический смысл.
Для каждого из тел справедлив закон сохранения момента количества движения вокруг центра инерции. В векторной форме уравнение вращательного движения вокруг центра инерции тела относительно произвольной опорной системы координат имеет вид
 , (2.1)
, (2.1)
где  – вектор главного момента количества движения i -го тела относительно центра инерции с;
– вектор главного момента количества движения i -го тела относительно центра инерции с;  – вектор угловой скорости расчетной системы координат (
– вектор угловой скорости расчетной системы координат ( , если система координат инерциальная);
, если система координат инерциальная);  – главный момент заданных сил;
– главный момент заданных сил; 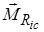 – момент реакции опор.
– момент реакции опор.
Выражение (2.1) можно записать в скалярной (матричной) форме[1]:
 , (2.2)
, (2.2)
где  – кососимметрическая матрица, необходимая для выполнения векторного умножения;
– кососимметрическая матрица, необходимая для выполнения векторного умножения; 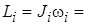
 (
( – тензор инерции тела,
– тензор инерции тела,  ,
, 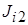 ,
,  – моменты инерции i ‑го тела относительно связанных с ним осей,
– моменты инерции i ‑го тела относительно связанных с ним осей, 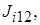

 – центробежные моменты инерции).
– центробежные моменты инерции).
В случае динамически уравновешенного тела центробежные моменты инерции равны нулю. Тогда тензор инерции представляет собой диагональную матрицу и после перемножения матриц получим:
 .
.
Уравнения движения двух или нескольких тел, объединенных в систему, получают, складывая геометрически левые и правые части уравнений (2.2), записанных для каждого тела, входящего в систему. Так, например, уравнение движения двух тел i и j, связанных через опоры, записывают следующим образом [1]:
 , (2.3)
, (2.3)
где  – матрица перехода от системы координат i к системе координат j.
– матрица перехода от системы координат i к системе координат j.
Последнее слагаемое  из выражения (2.3), если в системе есть следующее тело
из выражения (2.3), если в системе есть следующее тело  , связанное с j ‑м, состоит из
, связанное с j ‑м, состоит из

Перепроектировав (2.2) на систему координат, связанную с телом j, умножая обе части на  и заменяя
и заменяя  на
на 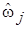 , выразим из (2.2)
, выразим из (2.2)  и подставим в (2.3):
и подставим в (2.3):
 .
.
Получим уравнение движения системы тел i и j в проекциях на систему координат, связанную с телом j:
 . (2.4)
. (2.4)
Это эквивалентно тому же, что умножить выражение (2.2) на  и геометрически сложить, заменяя
и геометрически сложить, заменяя  на
на 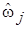 .
.
Выбирая в (2.4) строку, соответствующую оси вращения тела j, получим уравнение, не содержащее неизвестной реакции связи  .
.






