Подавление межсимвольной интерференции

В узкополосных (т.е. не использующих сложные сигналы) системах многолучевые компоненты, имеющие различную вре­менную задержку, не могут быть разделены (по крайней мере, без серьезных энергетических потерь) с помощью алгоритмов типа RAKE. В результате наложения запаздывающей копии сиг­нала, модулированного цифровым потоком данных, на опере­жающую текущая посылка последней искажается предыдущей посылкой запаздывающей копии. Возникающая таким образом специфическая помеха называется межсимвольной интерфе­ренцией (МСИ).

Обратимся вновь к модели манипулированного сигнала (4.1)

При максимальном времени рассеяния T_max возможно нало­жение друг на друга вплоть до

посылок. к примеру,

для стандарта GSM-900 Т_ь ≈ 3,7 мкс, а максимальное время рас­сеяния обычно принимается равным T_max = 16 мкс. При этом в при­емнике возможно наложение до М = 6 переданных посылок. Очевидно, что МСИ существенно затрудняет декодирова­ние принимаемых сигналов и приводит к увеличению частоты би­товых ошибок. К настоящему времени разработан ряд методов борьбы с МСИ. Коротко рассмотрим основные из них.

Алгоритм Витерби

В цифровых системах мобильной связи передача инфор­мации производится поэлементно с некоторым фиксированным интервалом между последовательными посылками.

В простейшем случае текущая наблюдаемая приемником посылка зависит только от текущей переданной. При этом опти­мальным (в смысле минимизации средней вероятности ошибоч­ного декодирования сообщения) является посимвольный прием, в процессе которого решение о значении каждой переданной посылки принимается отдельно, независимо от предыдущих и по­следующих посылок.

При наличии МСИ, однако, ситуация не столь проста, по­скольку каждое наблюдение определяется наряду с текущей так­же и предыдущими посылками. Тем самым в наблюдаемом сиг­нале проявляется зависимость от прошлого, т.е. память, подоб­ная, к примеру, той, что вводится в сигнал искусственно при ис­пользовании любых разновидностей частотной манипуляции с непрерывной фазой (см. гл. 4), а также сверточного кодирова­ния, рассматриваемого в следующей главе.

Посимвольный прием при этом не является оптимальным и уступает так называемому "приему в целом", при котором ре­шение о принятом сообщении выносится по результатам совме­стной обработки многих последовательных посылок. Поскольку сложность соответствующего приемника экспоненциально растет с памятью, его практическая реализация может оказаться про­блемной. Алгоритм Витерби, первоначальным назначением кото­рого было декодирование сверточных кодов, во многих случаях заметно упрощает процедуру "приема в целом" и потому часто применяется для борьбы с межсимвольной интерференцией.

 

Пусть наблюдаемый в /-й момент времени отсчет (6.16)

где s_j - отсчет полезного сигнала, искаженного МСИ; n_j- шумовой отсчет, являющийся гауссовской случайной величиной с нулевым средним.

Как отмечалось выше, МСИ возникает в многолучевом ка­нале за счет наложения копий сигнала, сдвинутых друг относи­тельно друга во времени из-за различия протяженности трасс распространения сигналов по отдельным лучам.

Пусть МСИ создается М дополнительными лучами. Тогда /-й сигнальный отсчет окажется линейной комбинацией /-го (а_i) и М предыдущих информационных символов: (6.17)

где a_k - коэффициент, отражающий вклад k-го луча.

Другими словами, информационный сигнал на /-м шаге яв­ляется результатом линейного кодирования вектора состояния, однозначно определяемого последовательностью переданных информационных символов

Следовательно, при конечном числе интерферирующих лу­чей (что имеет место в любой практической системе) МСИ можно рассматривать как выход устройства с конечным числом состояний [38]. Это позволяет выход канала с МСИ представить в виде кодовой решетки.

Такая кодовая решетка в бинарном случае содержит 2^м узлов (состояний). Из каждого узла выходят 2 ребра в соседние состояния, соответствующие различным значениям информацион­ного символа а_j. При этом каждое ребро может быть маркированосвоим значением отсчета s,, показывающим (в соответствий с (6.17)), как состояние вместе с текущим переданным символом а_j отражается в закодированном (через МСИ) сигнале. Получаемая кодовая решетка аналогична решетке сверточного кода, рас­сматриваемого в следующей главе. Отличие состоит в том, что значения отсчетов s_j, маркирующие ребра, являются действа тельными числами (а не двоичными словами). Демодулятор должен оценить переданные символы а_j, т.е. состояния.). Как известно, если помехой является АБГШ, то максималь­но правдоподобной оценкой

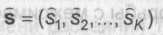
детектируемой последовательности

будет та, которая минимизиру­ет евклидово расстояние (6,18)

где К - объем наблюдаемой последовательности (количество декодируемых информационных символов).

В общем случае необходимо было бы вычислять расстоя­ния для всех возможных последовательностей (2^К в бинарном случае). Однако наличие памяти в сигнале (зависимость отсчета s_j, от состояния демодулятора А„ вводимая за счет МСИ) позволяет, используя алгоритм Витерби, уменьшить число анализируемых последовательностей.

Алгоритм Витерби является рекуррентным алгоритмом по­следовательного поиска пути на решетке, обеспечивающим мак­симально правдоподобное декодирование сигнала.

Демодулятор Витерби на каждом шаге (при приеме очеред­ного сигнального интервала) сравнивает наблюдаемые отсчеты y_j, с маркировкой входящих ребер s_j, для каждого узла, оставляя из двух путей один ("выживший"), имеющий наименьшую метрику (евклидово расстояние). После этой процедуры на новом шаге кодовая решетка содержит также 2^м узлов.

По прошествии времени в несколько длительностей памя­ти с вероятностью, очень близкой к единице, оказывается, что все выжившие пути исходят из одного узла [38]. Тогда состояние демодулятора, соответствующее этому узлу, может быть выдано как решение (оценка информационных символов). Таким обра­зом, с некоторой задержкой выдается оценка "старых символов^{^}.

Далее процесс продолжается по той же схеме. С приемом нового отсчета картинка сдвигается на один шаг (декодирован­ный символ исключается из анализа и добавляется вновь приня­тый). При этом в дальнейшем анализе используются только вы­жившие пути, запомненные ранее.

Вычислительная сложность алгоритма Витерби экспонен­циально возрастает с величиной временного рассеяния в канале. Для каждого нового принимаемого символа в бинарном случае необходимо вычислять 2^М+1 метрик. Для каналов с большим вре­менем рассеяния это может стать серьезным препятствием при практической реализации алгоритма.

Более подробно алгоритм Витерби рассмотрен, например, в [38], а также в следующей главе применительно к декодирова­нию сверточных кодов.