Принцип действия одноосной СП
Кинематическая схема и принцип действия
Одноосной силовой СП
Одноосной силовой СП называют гироскоп с тремя степенями свободы с сильной (жесткой) межрамочной коррекцией, благодаря которой кожух гироскопа может поворачиваться только на малые углы [2].
Двух- и трехосные силовые СП обычно можно рассматривать как совокупность двух или трех независимых одноосных СП. Это позволяет, изучив подробно одноосные платформы, перейти к анализу двух- и трехосных с учетом их особенностей [6].
Схема одноосной силовой СП приведена на рис. 1.1, на котором приняты следующие обозначения: 1 – гиромотор; 2 – платформа; 3 – датчик моментов (ДМ); 4, 5 – датчики угла (ДУ); 6 – стабилизирующий двигатель (СД); 7 – усилитель; 
– оси, связанные с платформой 2; 
– ось стабилизации; 
– ось прецессии; 
– угол прецессии; 
– угол поворота платформы 2 относительно объекта. На платформе закреплен стабилизируемый объект. Предположим, что относительно оси стабилизации 
действует постоянный возмущающий момент 
. Под действием этого момента гироскоп начинает прецессировать со скоростью 
так, чтобы вектор кинетического момента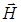 
совместился с вектором 
по кратчайшему пути. При этом величина угловой скорости прецессии 
находится из выражения
Благодаря прецессии гироскопа возникает гироскопический момент, определяемый согласно правилу Жуковского: при любом изменении углового положения в пространстве главной оси гироскопа с угловой скоростью возникает гироскопический момент, образующий с векторами и 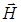правый трехгранник:
, 
,
где 
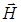– угол между векторами и 
.
Если в начальный момент времени угол прецессии 
, то 
, т. е. 
. Таким образом, возникающий гироскопический момент 
уравновешивает возмущающий момент , обеспечивая тем самым стабилизацию платформы. Отметим, что причиной, вызывающей прецессию, является возмущающий момент , а следствием прецессии – гироскопический момент .
В отсутствие стабилизирующего двигателя 6 прецессия продолжалась бы до совмещения вектора 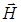с осью . Однако по мере прецессии гироскоп поворачивается на угол , и с датчика угла 4 начинает сниматься сигнал, пропорциональный углу , который после усиления поступает на стабилизирующий двигатель 6. Последний прикладывает к платформе вращающий момент, который: 1) компенсирует возмущающий момент , прекращая прецессию; 2) уменьшает угол до нуля (межрамочная коррекция). Датчик моментов 3 служит для начальной выставки платформы 2 за счет прецессии вокруг оси стабилизации, а также в штатном режиме для коррекции стабилизированных платформ, т. е. для управления положением платформы в пространстве.
Влияние качки основания на характер движения СП (Влияние вибраций основания на характер движения СП)
Влияние качки основания
Пусть объект совершает по оси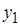 
регулярную качку по закону:
(6.1)
Качка (6.1) оказывает влияние на СП через возмущающий момент 
:
(6.2)
где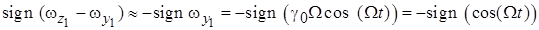 
. Если разложить полученную нелинейную функцию 
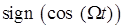в ряд Фурье, получим [5]:
, (6.3)
где высшие гармоники быстро убывают по амплитуде.
После подстановки (6.3) в (6.2) будем иметь:
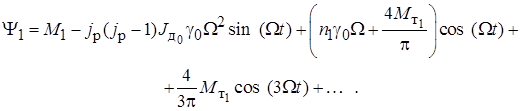
В общем виде первую гармонику можно представить как
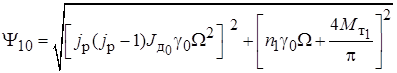. (6.4)
На рис. 6.1 представлено влияние момента 
на 
. Учет только первой гармоники ошибочен. Можно показать, что погрешность стабилизации определяется не только моментом, но и скоростью его изменения:
,
т. е. амплитуды высших гармоник не убывают.
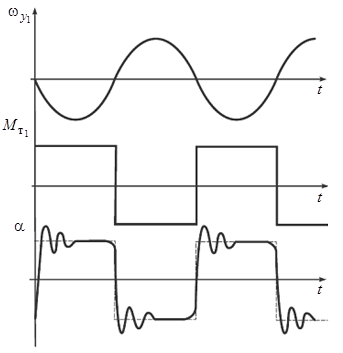
Рис. 6.1
Итак, по оси стабилизации действует периодический возмущающий момент с амплитудой, описываемой выражением (6.4), обусловленный влиянием вязкого и сухого трения и инерционностью СП по оси стабилизации. Данный момент, как и 
, должен компенсироваться двигателем, но при этом возникают дополнительные динамические погрешности.
