Метод статистических испытаний основан на моделировании (имитации) реальных процессов ТО, которые имеют вариацию, т.е. случайны [1]. Определение оптимальной периодичности ТО  данным методом существенно сокращает объем и стоимость экспериментов, а также продолжительность вычислительного процесса, так как моделирование при этом производится на ЭВМ. Исходным материалом для моделирования служат как фактические данные, полученные при наблюдении, так и законы распределения случайных величин.
данным методом существенно сокращает объем и стоимость экспериментов, а также продолжительность вычислительного процесса, так как моделирование при этом производится на ЭВМ. Исходным материалом для моделирования служат как фактические данные, полученные при наблюдении, так и законы распределения случайных величин.
Схема моделирования сводится к следующему (рис 5). На основании опыта и по существующим автомобилям-аналогам подбирается ряд значений оптимальных периодичностей ТО анализируемой операции. На следующем шаге на базе эксплуатационных (подконтрольных) испытаний партии исследуемых автомобилей производится расчёт наработки до отказа анализируемого КЭ автомобиля, для которого определяется 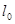 . С использованием полученной информации формируются два массива данных: массив наработок до отказа – [
. С использованием полученной информации формируются два массива данных: массив наработок до отказа – [  ] и массив периодичностей ТО – [
] и массив периодичностей ТО – [  ]. Затем из массива наработок [
]. Затем из массива наработок [  ] случайным образом извлекается какое-то конкретное значение наработки на отказ
] случайным образом извлекается какое-то конкретное значение наработки на отказ  , а из массива периодичностей [
, а из массива периодичностей [  ] также случайным образом извлекается какое-то значение
] также случайным образом извлекается какое-то значение 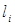 . Пара чисел
. Пара чисел  и
и 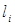 в подобных численных алгоритмах называется реализацией. Указанные величины сравниваются. При этом если получается
в подобных численных алгоритмах называется реализацией. Указанные величины сравниваются. При этом если получается  , то фиксируется отказ, который произошел раньше профилактического технического вмешательства; при
, то фиксируется отказ, который произошел раньше профилактического технического вмешательства; при 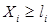 – фиксируется отсутствие отказа, что свидетельствует о том, что операция ТО выполнена раньше, чем произошёл отказ. Процесс моделирования повторяется многократно и в итоге получают оценку вероятности отказа. Сравнивают её с нормативной, например, величиной риска для конкретного КЭ автомобиля. Если при моделировании вероятность отказа оказалась больше или меньше нормативной, то корректируют массив периодичностей и повторяют моделирование до получения требуемой вероятности безотказной работы данного КЭ автомобиля. Среднее значение из массива периодичностей ТО будет являться искомой величиной оптимальной периодичности
– фиксируется отсутствие отказа, что свидетельствует о том, что операция ТО выполнена раньше, чем произошёл отказ. Процесс моделирования повторяется многократно и в итоге получают оценку вероятности отказа. Сравнивают её с нормативной, например, величиной риска для конкретного КЭ автомобиля. Если при моделировании вероятность отказа оказалась больше или меньше нормативной, то корректируют массив периодичностей и повторяют моделирование до получения требуемой вероятности безотказной работы данного КЭ автомобиля. Среднее значение из массива периодичностей ТО будет являться искомой величиной оптимальной периодичности  исследуемого КЭ автомобиля.
исследуемого КЭ автомобиля.
Следует добавить, что при этом наработка на отказ и периодичности представляются в вероятностной форме со всеми необходимыми характеристиками закона распределения Гаусса, которым и соответствуют эти величины на практике. Речь идёт об  ,
,  ,
,  ,
, 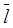 ,
,  и т.д.
и т.д.
Данный метод является более предпочтительным чем по допустимому уровню безотказности.
Метод статистических испытаний нельзя обособить от группы аналитических методов, скорее он реализует один из них или совокупность методов. По мере усложнения модели СТОР и исходной неопределённости при определении периодичности ТО возникает необходимость применения метода статистических испытаний вместо аналитических методов. Привлекательность статистического моделирования объясняется практически отсутствием ограничений при математическом описании СТОР автомобилей. Этот метод позволяет учитывать множество факторов различной природы, также он является наиболее пригодным для машинной реализации.
В рассматриваемом примере могут быть введены еще две варьируемые величины — стоимость или трудоемкость выполнения профилактической и ремонтной операции, что позволяет при каждой реализации определить суммарные удельные затраты на ТО и ремонт и сравнить различные периодичности ТО также и по экономическому критерию.
В настоящее время все большее распространение получают методы, основанные на имитационном моделировании. Это связано с развитием персональных ЭВМ, которые существенно сокращают объем и стоимость экспериментов, а также продолжительность вычислительного процесса.
Появление простых языков программирования, облегчение используемых в них алгоритмов позволяют разработать программное обеспечение, в основе которых лежит метод статистических испытаний (Монте-Карло).







