Номінальна та ефективна ставка складних відсотків. Поняття неперервного складного відсотку та сили росту

У фінансових обчисленнях за правилом складних про­центів, для врахування ефекту реінвестування,у випадках, коли протягом одного періоду часу відбувається декілька нарахувань процентів, вводять поняття ефективної та номінальної ставок до­хідності.

Ставку складних відсотків і, що входить у рівняння (3.1) та (3.17) називають номінальною ставкою.

Ефективна ставка і_е визначає, яку річну ставку складних відсотків необхідно встановити, щоб отримати такий самий фінансо­вий результат, як і за m-разового нарахування відсотків за рік за ставкою і/т. Іншими словами, це виражена у відсотках сума всіх необхідних виплат, які можна отримати за фінансово-кредитною угодою.

Формула визначення ефективної ставки відсотку наступна:

 

(3.18)

 

Зауважимо, що коли т > 1, то ефективна ставка більша за но­мінальну, причому, чим більша величина т (чим частіше нараховують проценти) тим вищою є ефективна ставка дохідності, отже, й тим швидше відбувається процес нарощення.

 

Якщо при нарощенні коштів за формулою (3.17) часовий ін­тервал між виплатами відсотків наближається до нуля, тобто проценти виплачують та реінвестують безперервно, то можна об­числити граничне значення ефективної ставки дохідності за ві­домої номінальної ставки дохідності. З метою таких обчислень вводять поняття неперервного склад­ного відсотку.

Неперервна складна ставка дохідності — це така ефективна ставка, за якою відсотки виплачують та реінвестують неперервно, тобто кількість періодів нарахувань відсотків прямує до нескінченості.

У деяких виданнях джерелах в разі неперер­вного нарощення відсотків застосовують інший термін для опису неперервних складних ставок дохідності — силу росту.

Сила росту характеризує відносний приріст нарощеної суми за нескінченно малий проміжок часу. Вона може бути постійною або змінюватись в часі.

Для неперервних складних відсотків формула (3.17) має вигляд:

 

(3.19)

 

Отже, незалежно від тривалості фінансової угоди п, частоти нарахувань відсотків т та номінальної ставки дохідності і, множ­ник нарощення складних відсотків ніколи не перевищуватиме величину ℓ^і*n. Причому, у разі неперервного способу нарахуван­ня складних відсотків рівняння оцінки майбутньої вартості є експоненціальною функцією, а величина майбутньої вартості не залежить від частоти нарахувань т.

Слід зазначити, що більшість сучасних фінансових угод передбачає дис­кретне нарахування процентів, тому неперервні ставки дохідності на сьогодні мають дуже обмежене коло застосування.

Криві прибутковості

Будь-яка фінансово-економічна операція припускає використання процентної ставки. Для практика важливо уявити закономірність зміни розміру ставок залежно від певного фундаментального фактору. Імовірно, найбільш важливим з таких факторів є ризик неповерненнякоштів. Такий ризик залежить від ряду чинників, серед яких, найбільш важливим є строк операції. Так, при всіх інших рівних умовах позичка на п'ять років є більш ризикованою, ніж на два роки. Компенсувати ризик власникові грошей може підвищення прибутковості. Таким чином, залежність „прибутковість — ризик” приблизно можна охарактеризувати за допомогою залежності „прибутковість — час”, одержати яку для практичних цілей простіше. Таку залежність, представлену у вигляді графіка, називають кривої прибутковості (рис.3.2).

Y A

 

Б

 

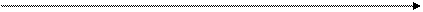Рис. 3.2. Криві прибутковості t

 

На графіку по вертикалі відкладають прибутковість (Y), по горизонталі — строк (t). Якщо графік охоплює широкий діапазон строків (як короткострокові, так і довгострокові операції), то для виміру строку застосовують логарифмічну шкалу.

Отже, крива прибутковості характеризує зміну прибутковості однорідних фінансово-економічних операцій або фінансових інструментів (наприклад, облігацій, акцій тощо) залежно від їхнього строку. Конкретна крива прибутковості відповідає реальної ситуації, що склалася на грошово-кредитному ринку, і характерна для короткого періоду часу. Зміна ситуації змінює і форму кривої та її положення на графіку.

Для нормальних економічних умов крива прибутковості має форму кривої Ана рис. 3.2. Прибутковість зростає в міру збільшення терміну інвестицій. Причому кожна наступна одиниця приросту строку дає все менше збільшення прибутковості. Таку криву називають позитивною, або нормальною, кривою прибутковості. Нормальна форма кривої спостерігається в умовах, коли інвестори враховують такі фактори, як скорочення ступеня ліквідності й зростання невизначеності фінансових результатів при збільшенні строку.

Крива прибутковості, близька до горизонтальної прямої (крива Б на рис. 3.2), вказує на те, що інвестори не беруть до уваги ризик, пов'язаний зі строком фінансової операції.

Іноді зустрічаються „негативні” і „згорблені” криві прибутковості. Перша відповідає зменшенню прибутковості в міру збільшення строку (нестабільність фінансового ринку), друга — падінню прибутковості після періоду деякого її росту.

Існують дві конкуруючі (а іноді доповнюючі) теорії, що пояснюють поведінку прибутковості — теорія ліквідності й теорія очікувань. Перша теорія зміну прибутковості пов'язує зі збільшенням ризику ліквідності в міру збільшення строку угоди. Саме з цієї позиції пояснюються позитивна й горизонтальна криві прибутковості.

Згідно із другою теорією стверджується, що форма кривої може розглядатися і як узагальнена характеристика очікувань інвесторів, їхньої поведінки в теперішній момент у зв'язку з очікуваннями змін процентних ставок у майбутньому. Однак інтерпретація форми кривої у цьому плані неоднозначна, оскільки доводиться брати до уваги принаймні дію двох факторів — ризику й очікування змін ставок.

Криві прибутковості одержали поширення як інструмент, що допомагає при розв'язку ряду інвестиційних проблем, зокрема, при порівнянні прибутковості різних фінансових інструментів (відображення на одному графіку декількох кривих прибутковості), корегуванню портфеля активів тощо.

Розглянемо на прикладі один із простих способів застосування кривої прибутковості.

Приклад 4. Припустимо, необхідно інвестувати деяку суму грошей на чотири роки. Причому, у інвестора є тільки два варіанти для цього: розмістити цю суму на депозиті відразу на весь строк або спершу на три роки, а потім на один рік. Нехай рівні процентних ставок відносяться до нормальної кривої прибутковості: за трирічними депозитами — 10%, за чотирирічними — 10,5% річних. Розмір ставки для депозиту на один рік (тобто на четвертий рік) у момент ухвалення рішення, невідомий. Який варіант розміщення коштів краще обрати інвестору?

 

Очевидно, що при виборі другого варіанта інвестор повинен мати результат не гірше, ніж при першому варіанті. Отже, завдання зводиться до визначення такого значення ставки для четвертого року, при якому обидва варіанти будуть рівноцінними (еквівалентними) у фінансовім відношенні, тобто визначені критичної, або бар'єрної ставки.

Позначимо як i₃ і і₄ рівні процентних ставок для депозитів на три й чотири роки, а через і₀ — невідому критичну ставку для річного депозиту. В силу фінансової еквівалентності результатів розміщення коштів множники нарощення для обох варіантів повинні бути рівними один одному. Звідси:

 

а, відповідно,

 

За даними прикладу знайдемо критичну ставку:

Таким чином, для того щоб інвестор зупинився на другому варіанті, він повинен очікувати, що через три роки ставка за однорідними депозитами буде не менш 12,014 %, тобто рівень ставок підвищиться. Відповідно, якщо він очікує, що ставка не досягне цього рівня, слід обрати перший варіант.