Методика обчислень за правилом складних відсотків

ТЕМА 3

СКЛАДНІ ВІДСОТКИ

1.	Методика обчислень за правилом складних відсотків
2.	Темп росту коштів за правилом складних відсотків
3.	Розрахунки за правилом складних відсотків в умовах змін вихідних параметрів
4.	Номінальна та ефективна ставка складних відсотків. Поняття неперервного складного відсотку та сили росту
5.	Криві прибутковості
6.	Конверсія валюти й нарощення складних відсотків

Методика обчислень за правилом складних відсотків

На користь вибору кожного з варіантів розрахунку відсотків (прості, складні) існують об'єктивні передумови, тому жодним з них не можна знехтувати та не розглядати взагалі. Правило простих процентів є простішим з погляду математичних розрахунків, а правило складних процентів — реалістичнішим в аспекті опису прикладних економічних задач.

Практика сучасних економічних відносин свідчить, що серед існуючих методик нарахування відсотків саме обчислення за пра­вилом складних процентів є основою переважної більшості фі­нансових операцій.

Правило складних відсотків (compound interest ) зазвичай засто­совують у середньо- та довгострокових фінансових угодах (строк більший від одного року), та у випадках, коли процен­ти не виплачують відразу після їх нарахування, а додають до основної суми боргу. Іншими словами, цей метод передбачає реінвестування коштів та капіталізацію відсотків.

Сутність методу нарахування за складними процентами поля­гає в тому, що наприкінці кожного періоду до основної суми грошей додають нараховані проценти й отримана таким чином сума грошей є вихідною для нарахування процентів у наступно­му періоді.

Отже, у разі нарощення за складними процентами база для нарахування в кожному наступному періоді змінюється, оскільки кожна наступна сума зростає на частку від попередньої.

В загальному вигляді, формулу нарощення за склад­ними відсотками (декурсивний метод нарахування) записують так:

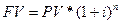(3.1)

 

Величину (1+і)ⁿ називають множником нарощення склад­них відсотків.

У формулі (3.1) для коректних обчислень за методом складних процентів величини і та п мають бути взаємоузгоджені (зведені до одних величин часу - років, місяців, днів тощо).

Приклад 1. Знайти майбутню вартість коштів за правилом складних відсотків, якщо теперішня вартість РV= 1000 грн., ставка дохідності і— 10 %, термін угоди – 3 роки.

За формулою (3.1) майбут­ня величина теперішньої суми 1000 грн. дорівнюватиме:

 

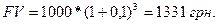
Для спрощення розрахунків у фінансово-економічних операціях використовують фінансові таблиці – таблиці процентних значень теперішньої та майбутньої вартості активів.

Визначення теперішньої або майбутньої вартості грошей за цими таблицями здійснюється за допомогою вже розрахованих множників (процентних факторів). Так, процентний фактор для визначення майбутньої вартості позначається FVIF (і,n), а теперішньої – PVIF (і,n).

В даному випадку формула визначення майбутньої вартості грошей набуває виразу:

(3.2)

 

Продовження прикладу 1. Розрахуємо майбутню вартість суми 1000 грн. за допомогою фінансових таблиць.

 

Послідовність нарощених за правилом складних відсотків сум становить геометричну прогресію.

Порівнюючи результати обчислень за простими процентами та складними відсотками, можна зробити висновок: Нарахування складних процентів рівнозначне нарахуванню прос­тих процентів з реінвестуванням коштів наприкінці кожного періоду.

 

Коли відома кінцева (майбутня) вартість, за правилом склад­них процентів можна обчислити приведену (теперішню) вартість, виконавши операцію дисконтування за формулою:

(3.3)

 

Аналогічно до вищезазначеного розмір теперішньої вартості за методикою складних відсотків можна розраховувати за допомогою фінансових таблиць. В такому випадку формула набуде вигляду:

(3.4)

 

Приклад 2. Розрахувати теперішню вартість1000 грн. під % ставку 10% за 3 роки.

 

 

У практиці фінансових обчислень за відомої початкової суми часто виникає питання оцінювання не кінцевої суми, а абсолют­ної різниці між кінцевою та початковою сумами — нарощеної величини. Наприклад, у задачах оцінювання ефективності інвестицій, цю нарощену величину можна трактувати як абсолютний прибуток від інвестування. За використання правила складних процентів цю нарощену величину називають розміром складного відсотку ІС та розраховують таким чином:

 

(3.5)

 

 

Продовження прикладу. За попередніх умов розрахувати роз­мір складного відсотку.

 

Знаючи за умовами попередніх розрахунків (приклад 1) майбутню вартість, розмір складного відсотку можна знайти як різницю між кінцевою та початковою сумами:

 

Розмір складного проценту перевищує розмір простого про­центу за рахунок того, що за методикою складних процентів на­прикінці кожного періоду відбувається реінвестування коштів.

 

Норма дохідності за використання правила складних процентів визначається за наступною формулою:

(3.6)

 

Розглянувши операції нарощення та дисконтування коштів, розглянемо також як здійснюють операцію утримання коштів за правилом складних процентів.

Операцію утримання складних процентів застосовують, зок­рема, у фінансових обчисленнях щодо деяких видів боргових зо­бов'язань зі строком погашення, більшим за один рік.

Теперішню вартість, яку із застосуванням складної ставки дисконтування і обчислюють за формулою (3.3), використовуючи складну облікову ставку d можна знайти так:

(3.7)

 

Зазначимо, що вираз (3.7) має економічний сенс лише коли складна облікова ставка d є меншою за 100 %.

Величину (1- d)ⁿ називають множником утримання складних процентів.

Оцінювання дохідності операції утриман­ня складних процентів відбувається за формулою:

(3.8)

 

Серед усіх розглянутих ставок дохідності, саме обчислення складної облікової ставки дасть найнижчий результат.

З виразів (3.6) та (3.8) можна знайти наступне співвідношення між складною ставкою і та складною обліковою ставкою d:

 

(3.9)