Чётные и нечётные функции.

Функция у = f (х) называется чётной, если для любого х из области определения функции выполняется равенство f (- х)= f (x).	у = f (х) чётная Û " х Î D (y) Þ f (- х)= f (x)
Функция у = f (х) называется нечётной, если для любого х из области определения функции выполняется равенство f (- х)=- f (x).	у = f (х) нечётная Û " х Î D (y) Þ f (- х)=- f (x) или у = f (х) нечётная Û " х Î D (y) Þ f (х)=- f (- x)
Из определения следует, что область определения D (y) как чётной, так и нечётной функции должна обладать следующим свойством: если х Î D (y), то и -х Î D (y)(т. е. D (y) - симметричное относительно 0 множество).
Функция у = f (х) которая не является ни чётной, ни нечётной называется функцией общего вида.

 

Если функция является чётной, то её график симметричен относительно ________________________. Обратное утверждение _____________________.

Итак, функция является чётной тогда и только тогда, когда её график симметричен относительно оси Оу.

Если функция является нечётной, то её график симметричен относительно ________________________. Обратное утверждение _____________________.

Итак, функция является нечётной тогда и только тогда, когда её график симметричен относительно начала координат.

 

· Сумма чётных (нечётных) функций является чётной (нечётной) функцией.

· Произведение двух чётных или двух нечётных функций является чётной функцией.

· Произведение чётной и нечётной функции является нечётной функцией.

· Если функция f чётна (нечётна), то и функция ¹/ _f чётна (нечётна).

 

Задание 1. Продолжите утверждение:

Известно, что функция f (x) – нечётная функция, причём в точке (х ₀; f (х ₀)) функция имеет минимум,и х ₂< x ₁<0, причём на интервале (х ₂; х ₁) функция возрастает.

функция f (x) в точке (- х ₀; _____) имеет___________________;

функция f (x) в точке (- х ₀; _____) имеет___________________;

функция f (x) на интервале______________________________;

 

Известно, что функция f (x) – чётная функция, причём в точке (х ₀; f (х ₀)) функция имеет минимум,и х ₂> x ₁>0, причём на интервале (х ₁; х ₂) функция возрастает.

функция f (x) в точке (- х ₀; _____) имеет___________________;

функция f (x) в точке (- х ₀; _____) имеет___________________;

функция f (x) на интервале______________________________;

 

 

Задание 2. Выберите среди предложенных функции, которые следует исследовать на чётность или нечётность:

№	Пример функции	Область определения

 

Задание 3. Какие из следующих функций чётные, какие нечётные, а какие функции общего вида:

№	Пример функции	Область определения	Вид функции

 

 

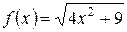
Задание 4. Выберите верные утверждения:

№	Утверждение	(+) (-)
	если f (x) – чётная, то её график симметричен относительно оси ординат
	если f (x) – не является чётной, то её график не симметричен относительно оси ординат
	если f (x) – не является чётной, то её график симметричен относительно оси ординат
	если f (x) – чётная, то её график симметричен относительно оси абсцисс
	если f (x) – не является чётной, то её график не симметричен относительно оси абсцисс
	если f (x) – не является чётной, то её график симметричен относительно оси абсцисс
	если f (x) – чётная, то её график симметричен относительно начала координат
	если f (x) – не является чётной, то её график не симметричен относительно начала координат
	если f (x) – не является чётной, то её график симметричен относительно начала координат
	если f (x) – нечётная, то её график симметричен относительно оси ординат
	если f (x) – не является нечётной, то её график не симметричен относительно оси ординат
	если f (x) – не является нечётной, то её график симметричен относительно оси ординат
	если f (x) – нечётная, то её график симметричен относительно оси абсцисс
	если f (x) – не является нечётной, то её график не симметричен относительно оси абсцисс
	если f (x) – не является нечётной, то её график симметричен относительно оси абсцисс
	если f (x) – нечётная, то её график симметричен относительно начала координат
	если f (x) – не является нечётной, то её график не симметричен относительно начала координат
	если f (x) – не является нечётной, то её график симметричен относительно начала координат
	существуют функции, являющиеся одновременно чётными и нечётными
	не существует функций, являющихся одновременно чётными и нечётными

 

Периодические функции.

Функция у = f (х) называется периодической, если существует число Т ¹0, такое, что для любого х из области определения функции выполняется равенство f (х + Т)= f (x).

Число Т называется периодом функции. Если Т – период функции, то её периодом является также и число – Т. Обычно под периодом функции понимают наименьший из положительных периодов, если такой период существует.

Задание 5. Известно, что функция f ( x ) – периодическая функция с периодом T. Запишите к каждой функции соответствующие им периоды:

 

№	Функция	Период		№	Функция	Период
	f (2 x)				f (4 x)
	f (0,2 x)				f (0,4 x)
	f (0,5 x)				f (0,25 x)
	f (2+ x)				f (3+ x)
	f (- x)				f (-2 x)
	f (2- x)				f (3- x)
	f (x +4)				f (x +2)
	f (2 x -5)				f (4 x +3)
	f (1,25 x)				f (2,5 x)
	f (4 x)+ f (3 x)				f (2 x)+ f (3 x)
	f (4 x +2)- f (3 x -1)				f (3 x -2)- f (2 x +1)
	f (4 x)· f (0,25 x)				f (5 x)· f (0,2 x)
	f (0,3 x)/ f (3 x)				f (4 x)/ f (0,4 x)
	f (-1,5 x)+ f (4 x)				f (1,2 x)+ f (-5 x)
	5 f (1-4 x)- f (0,2 x)				2 f (0,5 x)-5 f (2 x)
	f (4 x)· f (- x)				f (- x)· f (2-3 x)
	2 f (0,1 x)/ f (3 x)				3 f (0,4 x)/ f (2 x)
	f (0,5 x)+3 f (0,6 x)				f (0,3 x)+2 f (-0,2 x)
	f (x)-2 f (3 x)				f (4 x)-4 f (x)
	f (4 x)· f (0,3 x)				3 f (0,5 x)· f (5 x)

 

Задание 6. Построить в полярной системе координат:

j °                   r                     j °                 r

 

j °                   r                     j °                 r

 

Задание 7. Соотнести функции и построенные графики:

 

Задание 8. Построить в прямоугольной декартовой системе координат функцию заданную параметрически:

t °                   x                   y                     t °                 x                 y

 

Задание 9. Соотнести функции и построенные графики:

Решить в тетради:

Номера заданий	Страница в задачнике
43-71 (нечётные номера)	40-41

 

Полярные координаты позволяют рисовать намного более сложные и красивые фигуры. На протяжении многих лет ученые собирали информацию о формулах, рисующих разные фигуры. Многие фигуры получили свои названия. Список таких названий внушителен.

· Дельтоида

· Астроида

· Кардиоида

· Лимакона (Улитка Паскаля)

· Спираль Архимеда

· Логарифмическая спираль

· Кохлеоида

· Строфоида

· Freeth's Nephroid

· Овалы Кассини

· Лемниската Бернулли

 

Окружность радиуса R Уравнение в полярных координатах: r = R	Окружность радиуса R Уравнение в полярных координатах: r =2 R · cosj	Окружность радиуса R Уравнение в полярных координатах: r =2 R · sinj
Окружность радиуса R Уравнение в прямоугольных координатах: х 2 +у 2= R 2 параметрические уравнение:	Окружность радиуса R   Уравнение в прямоугольных координатах: (х - х 0)2 + (у - у 0)2= R 2
Лемниската Бернулли Уравнение в прямоугольных координатах: (х 2+ у 2)2 -а 2(х 2- у 2)2=0, где а >0 Уравнение в полярных координатах:	Трёхлепестковая роза Уравнение в полярных координатах: где а >0
Улитка Паскаля (a > b)   Уравнение в полярных координатах: r = b + a · cosj	Улитка Паскаля (a = b)   Уравнение в полярных координатах: r = b + a · cosj	Улитка Паскаля (a < b)   Уравнение в полярных координатах: r = b + a · cosj
Полукубическая парабола Уравнение в прямоугольных координатах: у 2= х 3 параметрические уравнение:	Астроида Уравнение в прямоугольных координатах: параметрические уравнение:
Кардиоида Уравнение в полярных координатах: r = a ·(1+ cosj), где а >0 Кардиоида – частный случай улитки Паскаля (a = b)	Спираль Архимеда Уравнение в полярных координатах: r = a · j, где а >0
Циклоида Параметрические уравнение: , где а >0 Циклоида – это кривая, которую описывает фиксированная точка окружности, катящаяся без скольжения по неподвижной прямой.