Параллельными называются две прямые, которые лежат в одной плоскости и не имеют общих точек.
Проекции параллельных прямых на любую плоскость (не перпендикулярную данным прямым) - параллельны (рис.33).

| 
| ||
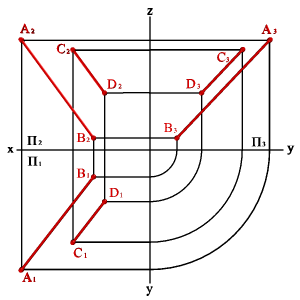
| а) модель | б) эпюр | ||
| Рисунок 33. Параллельные прямые |
Если AB//CD то A1B1//C1D1; A2B2//C2D2; A3B3//C3D3. В общем случае справедливо и обратное утверждение.
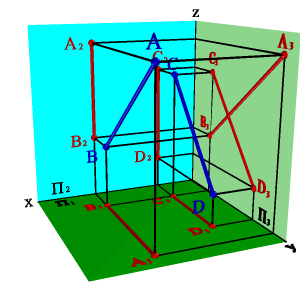
Особый случай представляют собой прямые, параллельные одной из плоскостей проекций. Например, фронтальные и горизонтальные проекции профильных прямых параллельны, но для оценки их взаимного положения необходимо сделать проекцию на профильную плоскость проекций (рис. 34). В рассмотренном случае проекции отрезков на плоскость П3 пересекаются, следовательно, они не параллельны.
Решение этого вопроса можно получить сравнением двух соотношений если:
А2В2/ А1В1= С2Д2/ С1 Д1 Þ АВ//СД
А2В2/ А1В1¹ С2Д2/ С1Д1Þ АВ#СД
| 
| ||
| а) модель | б) эпюр | ||
| Рисунок 34. Прямые параллельные профильной плоскости проекций |
Пересекающиеся прямые.
Пересекающимися называются две прямые лежащие в одной плоскости и имеющие одну общую точку.
Если прямые пересекаются, то точки пересечения их одноименных проекций находится на одной линии связи (рис. 35).

| 
| ||
| а) модель | б) эпюр | ||
| Рисунок 35. Пересекающиеся прямые |
В общем случае справедливо и обратное утверждение, но есть два частных случая:
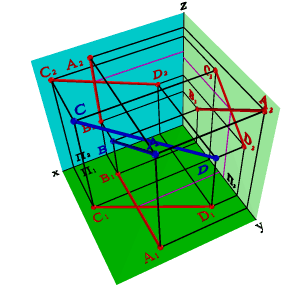
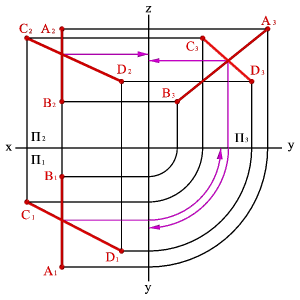
1. Если одна из прямых параллельна какой-либо из плоскостей проекций, например, профильной (рис.36), то по двум проекциям невозможно судить об их взаимном расположении. Так горизонтальная и фронтальная проекции отрезков АВ и СД пересекаются, причем точка пересечения проекций лежит на одной линии связи, однако сами отрезки не пересекаются, потому что точка пересечения профильных проекций этих отрезков не лежит на одной линии связи с точками пересечения их горизонтальной и фронтальной проекций.
| 
| ||
| а) модель | б) эпюр | ||
| Рисунок 36. Одна из прямых параллельна профильной плоскости проекций |
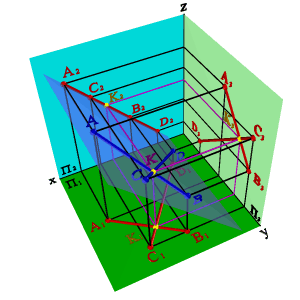
2. Пересекающие прямые расположены в общей для них проецирующей плоскости, например перпендикулярной фронтальной плоскости проекций (рис. 37).
О взаимном расположении прямых, лежащих в этой плоскости, можно судить по одной горизонтальной проекции (А 1 В 1∩ С 1 D 1Þ АВ∩СD).
| 
| ||
| а) модель | б) эпюр | ||
| Рисунок 37. Пересекающиеся прямые расположены в фронтально проецирующей плоскости |
Скрещивающиеся прямые
Скрещивающимися называются две непараллельные прямые не лежащие в одной плоскости.






