Обработка результатов косвенных измерений

Косвенные измерения – измерения, в которых искомое значение величины определяется на основании известной зависимости между этой величиной и величинами, полученными в результате прямых измерений.

Требуется оценить значение величины Y, связанной с измеренными величинами значениями x₁,…, x₂,…,x_k,Y=f(x₁,…, x₂,…,x_k)

Задача сводится к нахождению оценки неизвестной величины Y, если при обработке результатов прямых измерений получены оценки

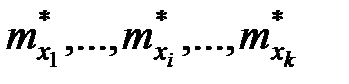величин x₁…x_k.

В большинстве случаев, исходное уравнение можно разложить в k – мерный ряд Тэйлора по различным степеням и получить оценки искомой величины. Дисперсия оценки величины Y будет достигать минимума в том случае, если дисперсии исходных величин (аргументов) будут минимальны.

Путем доказательства определено, что в качестве наиболее достоверного значения косвенной величины следует принимать значение, которое получено из формулы косвенной величины по средним арифметическим значениям аргументов.

. (8.15)

Дисперсия этой оценки по выборочным дисперсиям определяется по следующей зависимости:

, (8.16)

Где - коэффициент корреляции между значениями измеренных коэффициентов. Обычно =0, поскольку измерение аргументов производится неодновременно и с помощью различных средств измерения.

Статистическая дисперсия общей оценки определяется:

. (8.17)

Поскольку оценка косвенной величины получается путем математических расчетов по результатам нескольких аргументов, то она не будет точно соответствовать истинному значению величины – будет смещенной на величину систематической составляющей погрешности результата. Для некоррелированного измерения:

.

Для исключения этой систематической погрешности в рассчитанный результат нужно внести поправку q=- .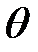

,

где 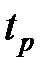- квантиль, величина которого определяет значение доверительного интервала и зависит от вида закона распределения итогового результата.

Если функция непрерывна, а результаты прямых измерений аргумента распределены нормально, то при заданной вероятности при достаточном количестве измерений для определения доверительного интервала используют распределение Стьюдента.

Если искомая величина является суммой двух величин (Y=x_i+x_j), то оценкой истинного значения косвенной величины является сумма оценок значений аргументов.

;

;

Доверительный интервал также рассчитывается в соответствии с законом Стьюдента.

Если косвенная величина является суммой m – аргументов. В этом случае оценками косвенной величины будут:

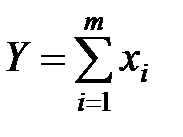; (8.20)

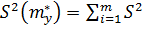()+ . (8.21)

Доверительный интервал определяется аналогично.